3.2 Вказівки щодо підготовки до заняття
Для успішного виконання даної лабораторної роботи необхідно розглянути методику побудови перехідної функції та АФХ, що наведені в розглянутих далі прикладах.
Приклад 3.2.1 Побудувати перехідну характеристику реальної диференціюючої ланки, яка задана рівнянням:
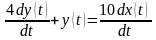і
.
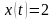Розв‘язок: загальний вигляд рівняння реальної диференціюючої ланки такий:
,
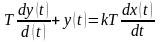де Т – постійна часу, с-1; k – передавальний коефіцієнт.
Якщо порівняти це рівняння з попереднім,
то можна записати: Т = 4 с-1; k
∙ Т = 10. Звідси:
.
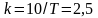Тепер значення k,
x(t),
T потрібно підставити
в рівняння перехідної функції [1]:
,
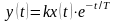тобто:
.
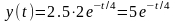Підставляючи різні значення t, підрахуємо значення у(t). Для обчислень та побудови перехідної функції використовуємо ПП „Mathcad”. Графік перехідної функції, побудований таким чином, зображений на рис.3.1, а дані обчислень зводимо в табл.3.1.
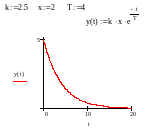
Рисунок 3.1 – Графік перехідної функції, побудований в ПП „Mathcad”
Таблиця 3.1 – Результати обчислень перехідної функції
t, с |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
y(t) |
5 |
3.033 |
1.839 |
1.116 |
0.677 |
0.41 |
0.25 |
0.151 |
0.09 |
0,056 |
0,034 |
Висновок: побудована перехідна характеристика дає можливість визначити сталу часу Т = 4 с-1 і передавальний коефіцієнт ланки k = 2.5.
Приклад 3.2.2 Маємо диференційне рівняння ланки:
.
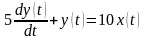Необхідно побудувати АФХ.
Розв’язок: запишемо диференційне рівняння в операторному вигляді, для цього замінимо в рівнянні ланки похідну d/dt на р, а змінну t на змінну р:
5 py(p)
+y(p) = 10x(p), або
.
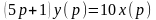З рівняння, записаного в операторному вигляді, знаходимо передавальну функцію як відношення вихідної величини до вхідної, зображених за Лапласом:
.
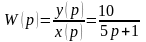АФХ отримуємо з передавальної
функції шляхом підстановки p → jω:
.
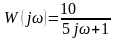Необхідно звільнитись від уявної одиниці в знаменнику, для цього домножуємо і чисельник, і знаменник на вираз, спряжений до знаменника:
.
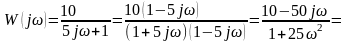
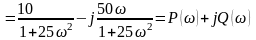Змінюючи ω від 0 до , отримуємо значення дійсної і уявної частин АФХ. Для обчислень та побудови АФХ використовуємо ПП „Mathcad”. Графік АФХ зображений на рис. 3.3, а дані обчислень зведені в табл. 3.2.
Таблиця 3.2 – Значення параметрів , Р(), Q()
ω |
0 |
0.1 |
0.2 |
0.6 |
1 |
2 |
5 |
10 |
Р() |
10 |
8 |
5 |
1 |
0.385 |
0.099 |
0.016 |
0.004 |
Q() |
0 |
-4 |
-5 |
-3 |
-1.923 |
-0.99 |
-0.399 |
-0.2 |
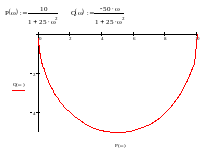
Рисунок 3.3 – АФХ інерційної ланки
Висновок: побудована АФХ має вигляд АФХ типової інерційної ланки 1-го порядку.
Приклад 3.2.3
Побудувати АФХ ланки 2-го порядку, яка
описується рівнянням:
.
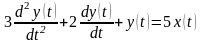Розв’язок: передавальна функція ланки, знайдена з диференційного рівняння, має вигляд:
.
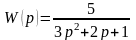Після підстановки jω замість р амплітудно-фазова функція матиме вигляд:
.
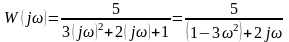Необхідно звільнитись від уявності в знаменнику. З цією метою домножимо чисельник і знаменник на спряжений вираз (1-3ω2)–2jω. Отримаємо:
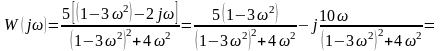
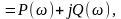
де Р()
=
;
Q()
=
.
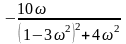Підставляючи значення ω від 0 до , знайдемо параметри Р() і Q() і будуємо АФХ. На рис.3.4 зображено АФХ, побудовану за допомогою ПП „Mathcad”, а результати розрахунків зведені в табл. 3.3.
Таблиця 3.3 – Результати розрахунків
ω |
0 |
0.5 |
1 |
2 |
3 |
4 |
5 |
Р() |
5 |
1 |
–5 |
–11 |
–13 |
–13.824 |
–14.231 |
Q() |
0 |
–4 |
–5 |
–4 |
–3 |
–2.353 |
–1.923 |
Висновок: побудована АФХ має вигляд типової АФХ ланки 2-го порядку.
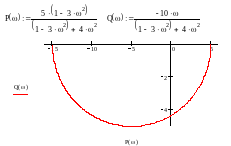
Рисунок 3.4 – АФХ ланки 2-го порядку
дОСЛІДЖЕННЯ СТІЙКОСТІ СаК ЗА КРИТЕРІЄМ гУРВІЦА