: ДОСЛІДЖЕННЯ СТАТИЧНИХ ХАРАКТЕРИСТИК типових динамічних ЛАНОК

Передавальні властивості ланок і систем в статичному режимі описуються за допомогою статичних характеристик. Статичною характеристикою ланки називають залежність його вихідної величини y від вхідної величини x в усталеному статичному режимі:

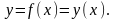(1.1)

Статична характеристика конкретної ланки може бути задана в формульному вигляді (наприклад, у вигляді алгебраїчної функції 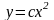) або у вигляді графіка (рис.1.1).

Так як статичний режим є частковим випадком динамічного режиму, то відповідна статична характеристика може бути одержана як частковий випадок диференційного рівняння:

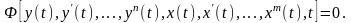(1.2)

Для цього необхідно в диференційному рівнянні ланки прирівняти всі похідні по часу до нуля (що відповідає визначенню поняття статичний режим) і тоді одержимо рівняння статики ланки:

(1.3)

Більшість конструктивних елементів автоматичних систем в статичному режимі характеризуються суворим однозначним співвідношенням між значеннями вхідної і вихідної величин. Ці ланки називаються статичними або позиційними. Але деякі елементи систем не володіють визначними передавальними властивостями в статичному режимі: при різних значеннях вхідної величини х вихідна величина у може приймати те саме значення, або навпаки при одному і тому ж значенні х величина у може приймати будь-які значення. Такі ланки називаються астатичними.

За виглядом статичних характеристик ланки діляться на лінійні і нелінійні. Статична характеристика лінійної ланки (рис. 1.1,а) описується лінійною функцією у = аx + b. В нелінійних ланках зв’язок між вхідною і вихідною величинами виражається, зазвичай, у вигляді степеневих функцій степеневих поліномів, дробових раціональних функцій і більш складніших функцій.

Нелінійні ланки, в свою чергу, розділяються на ланки з суттєво нелінійною статичною характеристикою (рис. 1.1,б) і ланки з несуттєво нелінійною (лінеаризуючою) характеристикою (рис. 1.1,в). Статична характеристика є несуттєво нелінійною, якщо вона описується неперервною диференційною функцією. Статична характеристика вважається суттєво нелінійною, якщо вона має ламаність або розриви.

а) – статична характеристика лінійної ланки;

б) – статична характеристика несуттєво нелінійної ланки;

в) – статична характеристика суттєво нелінійної ланки

Рисунок 1.1 – Статичні характеристики ланок АСК

В обмеженому діапазоні вхідна величина х може бути приблизно замінена (апроксимована) лінійною функцією. Приблизна заміна нелінійної функції лінійною називається лінеаризацією. Лінеаризація нелінійної характеристики правомірна, якщо в процесі роботи елемента його вхідна величина змінюється в невеликому діапазоні навколо деякого значення х₀. Цей діапазон і відповідну точку з координатами х₀ і у₀ називають робочим. Лінеаризацію гладких статичних характеристик здійснюють переважно за методом дотичних або найменших квадратів.

Передавальний коефіцієнт – це відношення зміни вихідної величини до зміни вхідної величини:

(1.4)

Розмірність передавального коефіцієнта – відношення розмінностей вихідної та вхідної величин відповідно.

Існує три види найпрoстіших з’єднань ланок автоматичних систем керування. Розглянемо їх.

1. Послідовне з’єднання – це з’єднання, при якому вихідна величина попередньої ланки є вхідною для наступної ланки. На рис. 1.2 наведена схема послідовного з’єднання ланок.

Рисунок 1.2 – Послідовне з’єднання ланок

Якщо ланки з'єднані послідовно і мають коефіцієнти k₁, k₂, k₃, то еквівалентний коефіцієнт системи дорівнює добутку цих коефіцієнтів:

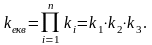(1.5)

2. Паралельне з’єднання – це з’єднання, при якому вхідна величина для всіх ланок є одна і таж сама, а вихідні величини додаються. На рис. 1.3 наведена схема паралельного з’єднання ланок.

Рисунок 1.3 – Паралельне з’єднання ланок

Я кщо ланки з'єднані паралельно і мають коефіцієнти k₁, k₂, k₃, то еквівалентний коефіцієнт дорівнює сумі цих коефіцієнтів:

(1.6)

3. Зворотній зв’язок – це з’єднання, при якому вихідна величина прямої ланки є вхідною для ланки зворотного зв’язку, а вихідна величина ланки зворотного зв’язку додається до вхідної величини прямої ланки.

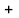
Рисунок 1.4 – З'єднання із зворотнім зв'язком

Еквівалентний коефіцієнт дорівнює:

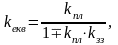(1.7)

де ”+” – зв'язок від’ємний; ”–” – зв'язок додатній.

Алгоритмічна структура будь-якої АСК є комбінацією трьох типових з’єднань ланок: послідовної, паралельної і обернено-паралельної дії.

1.2 Вказівки щодо підготовки до заняття

Для успішного виконання лабораторної роботи необхідно розглянути методику визначення передавального коефіцієнта ланок і їх з’єднань, що наведена далі в прикладах.

Приклад 1.2.1 Визначити коефіцієнт підсилення електронного підсилювача на основі даних, приведених в табл. 1.1

Таблиця 1.1 – Дані для побудови статичної характеристики електронного підсилювача

Uвх, В	0	0,5	2,0	5,0	8,0	10,0
Uвих, мВ	0	5	20	50	79,5	99,1

Розв’язок: будуємо статичну характеристику U_вих= f(U_вх) електронного підсилювача в ПП „Mathcad” (рис.1.5). Статичною характеристикою є залежність U_vux від U_vx. Як бачимо, статична характеристика є лінійною. Вибираємо на ній будь-яку ділянку, наприклад АВ, і розраховуємо зміну вхідної та вихідної величин на цій ділянці:

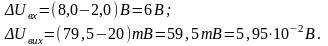
Визначаємо передавальний коефіцієнт:

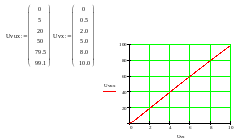
Рисунок 1.5 – Статична характеристика електронного підсилювача

Висновок: електронний підсилювач має безрозмірний коефіцієнт підсилення 0,01.

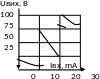
Приклад 1.2.2 Визначити передавальний коефіціент магнітного підсилювача, який має статичну характеристику, наведену на рис.1.6.

Розв’язок: визначаємо передавальний коефіціент на лінійній частині характеристики. Для цього знаходимо значення змін вхідної (струм) та вихідної (напруга) величин:

І_вх = (20 – 10) мА = 10 мА;

U_вих = (75 – 25)В = 50 В.

Розрахуємо передавальний коефіціент:

.

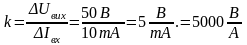
Рисунок 1.6 – Статична характеристика магнітного підсилювача

Висновок: магнітний підсилювач має передавальний коефіцієнт, рівний 5000 В/А.

Приклад 1.2.3 Визначити передавальні коефіцієнти на нелінійній статичній характеристиці, наведеній на рис. 1.7.

.

Рисунок 1.7 – Нелінійна статична характеристика

Розв'язок: проводимо дотичні в точках А і В, визначаємо пере­давальні коефіцієнти, використовуючи методику попередніх прикладів.

Приклад 1.2.4 Визначити еквівалентний передавальний коефіцієнт системи керування за її структурною схемою (рис.1.8) і передавальними коефіцієнтами ланок:

Рисунок 1.8 – Структурна схема системи керування

Розв’язок:

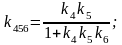
Приклад 1.2.5 Визначити передавальний коефіцієнт системи керування за її структурною схемою (рис. 1.9) і для таких значень передавальних коефіцієнтів ланок:

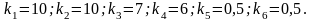
Рисунок 1.8 – Структурна схема системи керування

Розв’язок:

Визначення передавальних функцій об'єктів

2.1 Основні теоретичні положення

Найбільш поширеним методом опису і аналізу автоматичних систем є операційний метод. В основі методу лежить перетворення Лапласа, яке встановлює відповідність між функціями дійсної змінної і функ­ціями комплексної змінної р.

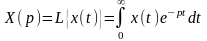, (2.1)

де x(t) – функція часу, яку називають оригіна­лом; x(p) – результат інтегрування, який називають зображенням функції x(t) по Лапласу.

Передавальною функцією W(p) називають відношення зображення по Лапласу вихідної величини до зображення по Лапласу вхідної величини при нульових початкових умовах:

. (2.2)

Передавальна функція елемента зв’язана з його імпульсною пере­хідною функцією перетворенням Лапласа:

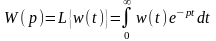. (2.3)

Для реальних елементів, що описуються звичайними диференційними рівняннями, передавальна функція представляє собою правильний раціона­льний дріб, у якого степінь многочлена чисельника менша або рівна степені многочлена знаменника. Всі коефіцієнти передавальної функції – дійсні числа, що характеризують параметри елемента.

Передавальна функція є функцією комплексної змінної р:

, яка може при деяких значеннях змінної р перетворюватись в 0 чи ∞. Значення змінної р, при якому функція W(р) перетворюєть­ся в 0, називають нулем, а значення, при якому перетворюється в ∞ – полюсом передавальної функції.

Для оцінки точності, стійкості і якості керування замкнутими системами необхідно знати їх рівняння статики і динаміки. Рівняння динаміки замкнутої системи можна отримати на основі сукупності рівнянь окремих елементів, що утворюють систему, шляхом послідовного виключення проміжних змінних. Найбільш зручним для розв'язку цієї задачі об'єднання математичних моделей елементів є метод структурних перетворень, згідно якого по структурі системи за допомогою декількох простих правил знаходять її загальну (еквівалентну) передавальну фун­кцію, а потім – відповідне рівняння динаміки.

Три головні правила перетворень структурних схем.

А. Передавальна функція послідовно з'єднаних ланок дорівнює добутку передавальних функцій всіх ланок, що входять у з’єднання:

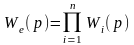. (2.4)

Б. Передавальна функція паралельно з'єднаних ланок дорівнює алгебраїчній сумі передавальних функцій всіх ланок, що входять у з'єднання:

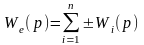. (2.5)

В. Передавальна функція з'єднання із від’ємним (додатнім) зворотнім зв’язком дорівнює передавальній функції прямої ланки, поділені на одиницю плюс (мінус) добуток передавальних функцій прямої ланки і ланки зворотнього зв’язку:

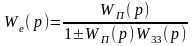. (2.6)

Алгоритмічну схему замкнутої системи керування (і саму систему) називають одноконтурною, якщо при її розмиканні в будь-якій точці утво­рюється ланцюг, що не містить паралельних з’єднань і зворотних зв'язків Утворений ланцюг називають розімкнутим контуром системи.

Характеристичне рівняння замкнутої одноконтурної системи пред­ставляє собою прирівняну до нуля суму одиниці і передавальної функції розімкнутого контуру:

1 + W_Pk(р) =0, (2.7)

де 1 + W_Pk(p) – власний оператор системи.