Применение производных в экономике.
Рассмотрим функцию издержек производства k=K(x) , где
k - издержки производства,
x – количество выпущенной продукции.
Если объем производства продукции увеличили на x, то количеству продукции x+x будут соответствовать издержки производства
k = k(x+x) - k (x) .
Предел отношения приращений
=K’(x)
называется предельными издержками
производства (показывает скорость
изменения K(x)).
Рассмотрим функцию u=u(x)
–
функция выручки от
продажи x
единиц продукции, тогда
- предельная выручка.
Пусть дана y=f(x), для которой известна производная y'=f '(x).
Эластичностью функции f(x) относительно x ( Ex(y) ) называют
,
т.е. 
.
Рассмотрим функцию
спроса по цене 
.
Тогда эластичность функции 
.
Эластичность спроса по цене показывает, на сколько процентов увеличится (уменьшится) спрос, если цена уменьшится (увеличится) на 1%.
Если Е=2, тогда если p увеличится на 1%, то Е показывает, что спрос уменьшится на 2%.
Дифференцируемость функции
Определение. Функция f(x) называется дифференцируемой в точке , если ее приращение в этой точке представимо в виде
,
где
A - число,
- приращение аргумента,
-
бесконечно малая функция при
.
Теорема. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство.
Необходимость.
Если функция дифференцируема в точке , тогда, по определению
.
Поделим обе части уравнения на . Получим
;
.
Таким
образом
, это значит, что функция имеет
производную.
Достаточность.
Если функция имеет производную равную А.. Это означает
,
. Откуда
; 
.
- б.м.
Таким образом 
, а это означает, что функция дифференцируема,
что и требовалось доказать.
Теорема. Если функция дифференцируема в точке, то она и непрерывна в этой точке.
Доказательство. Если функция дифференцируема в точке , то .
Вычислим предел 
Поскольку предел
, то функция
непрерывна в точке
, что и требовалось доказать.
Основные правила дифференцирования
Теорема.
Пусть функции
и
дифференцируемы в точке x,
тогда функции
;
;
также дифференцируемы в данной точке
и их производные равны
;
;
.
Доказательство. Будем использовать определение производных и следующие формулы
, 
.
1.
=
.
2.
=
, поскольку
.
3.
,
что и требовалось доказать.
Производные тригонометрических функций и логарифмической функции.
Рассмотрим
1)
;
.
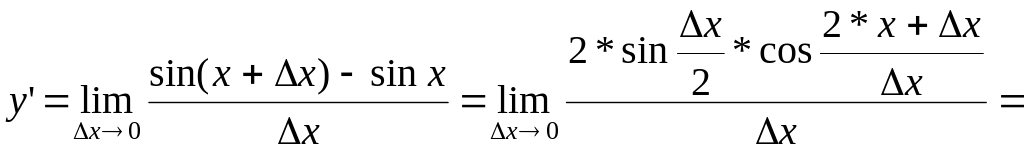
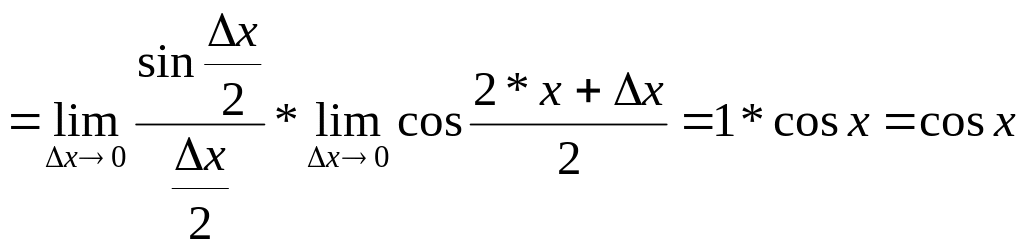2)
;
.
3)
.
4)
.
5)
;
.
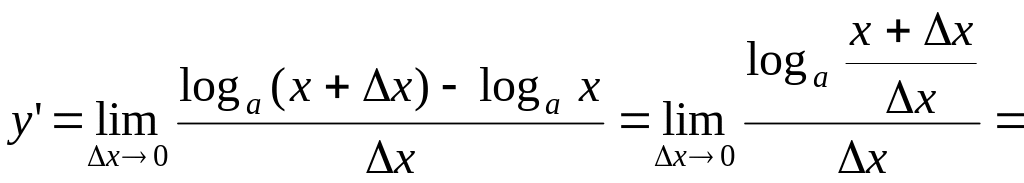
Использовали одно из следствий второго замечательного предела, согласно которому
.
Производная от обратной функции.
Пусть функция
имеет
обратную функцию 
.
Теорема.
Если
функция
имеет
в точке
производную
, то обратная
функция
имеет
в точке
производную, равную
.
Доказательство.
Для обратной функции
зададим приращение аргумента
, при этом приращение функции
.
Запишем отношение приращения функции к вызвавшему его приращению аргумента
.
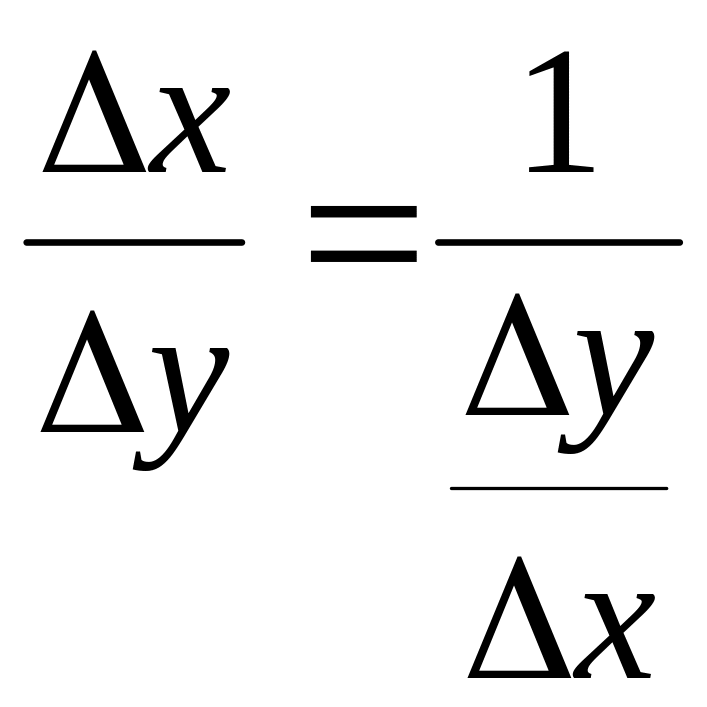Так как функция y=f(x)
имеет производную,
то она непрерывна в точке
и тогда предел
при
равен нулю ,
, то
, откуда 
,
что и требовалось доказать.