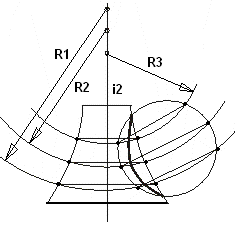
Знаки, обозначающие отношения между геометрическими фигурами:

// - параллельность двух геометрических фигур, - перпендикулярность, - скрещивающиеся прямые, - пересечение геометрических фигур (множеств), = - равны, совпадают или результат пересечения геометрических фигур, - конгруэнтность.

1.Метод ортогонального проецирования.

Гаспар Монж – Метод параллельного проецирования- ортогонального проец. – системы

прямоугольных проекций на взаимно перпендикулярных плоскостях. Обеспечивает

передачу на чертеже формы и размеров изображаемых предметов без искожения. Изложенный Монжем метод- метод параллельного проецирования (причем берутся прямоугольные проекции на две взаимно перпендикулярные плоскости проекций) -обеспечивая выразительность,точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.

Модель положения точки в системе π1 π2 π3 аналогична модели, к-ю можно построить, зная прямоугольные координаты (декартовы коорд.) т.е. числа, выражающие ее расстояния от трех взаимно перпендикулярных плоскостей- плоскостей координат.

Оси координат - прямые, по к-ым пересекаются плоскости координат.

Начало координат –О- точка пересечения осей.

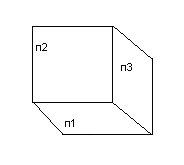
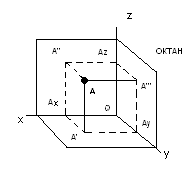Плоскости координат в своем пересечении

Образуют восемь трехгранных углов ,деля пространство на 8 частей – октанов .

Аx- абсцисса выразится числом АА’’’ или = ему отрезку АxО на оси x с некоторым отрезком,

взятым за единицу масштаба. Соответственно-

Аy-ордината. Аz-аппликата.

2.Точки излома- в к-ых происходит изменение знака с + на - , и наоборот.

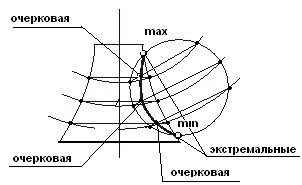
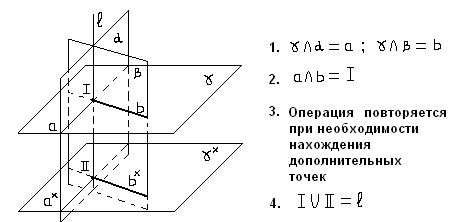
3. Метод вспомогательных секущих плоскостей.

Если прямая общего положения пересекает плоскость общего положения, то для нахождения точки пересечения прямой с плоскостью выбираем наиболее подходящий посредник, строим этот посредник на эпюре, находим прямую, определяем точку, решаем

вопрос видимости прямой относительно плоскости.

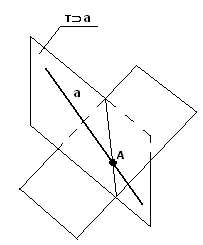
Прямая линия общего положения. Прямая, не параллельная ни одной из плоскостей проекций.

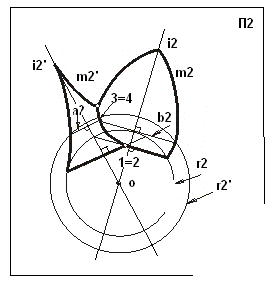
Метод концентрических сфер-посредников.

Способ сфер-посредников применяют чаще всего для построения линий пресечения поверхностей вращения, реже для циклических поверхностей общего вида. В основе лежат свойства соосных поверхностей вращения (и сферы). Концентрические сферы- посредники можно применять, если оси поверхностей вращения пересекаются, а их общая плоскость симметрии параллельна плоскости проекции. Если условие не выполняется, то следует ввести дополнительную плоскость проекции, параллельную обшей плоскости симметрии, решив задачу в новой плоскости, вернуться в исходную.

Метод эксцентрических сфер-посредников.

Если в состав объекта входит сфера, то в качестве посредников можно применять как концентрические, так и эксцентрические сферы с центрами О2, О3, О4 , расположенными обязательно на оси вращения поверхности общего вида. Эксцентрические сферы-посредники можно применить, если заданными поверхностями являются - поверхность вращения и циклическая (общего вида), у к-ых общая плоскость симметрии параллельна плоскости проекции.