19) Прямая в пространстве: общие уравнения прямой; векторное уравнение прямой; параметрические уравнения прямой; угол между прямыми; взаимное расположение двух прямых.

Векторное уравнение прямой:

Параметрическое уравнение:

Угол между прямыми можно найти с помощью направляющих векторов.

Условия параллельности:

Условия перпендикулярности:

20) Прямая в пространстве: канонические уравнения прямой; уравнение прямой, проходящей через две точки; переход от общих уравнений прямой к каноническим.

Каноническое уравнение прямой:

В частном случае, когда направляющий вектор единичный:

Уравнение прямой. Проходящей через две точки.

• .

Переход от общих уравнений к каноническим:

21) Прямая и плоскость в пространстве: взаимное расположение прямой и плоскости; точка пересечения прямой и плоскости; угол между прямой и плоскостью; пучок плоскостей.

Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой и вектор нормали перпендикулярны.

Прямая и плоскость перпендикулярны, когда вектор нормали и направляющий вектор параллельны.

Для нахождения точки пересечения прямой и плоскости нужно представить уравнение прямой в параметрическом виде, затем подставить значения x, y, z в уравнение плоскости. ->

При этом векторы должны быть не перпендикулярны и не параллельны.

Для нахождения угла между прямой и плоскостью:

Пучок плоскостей:

22) Прямая на плоскости: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору; общее уравнение прямой; исследование общего уравнения прямой; взаимное расположение прямых, заданных общими уравнениями.

Уравнение:

Даны точка и вектор ,

Т.к вектор и прямая перпендикулярны, их скалярное произведение равно нулю, т.е, в координатной форме: Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Общее уравнение прямой -

Исследование прямой: При A=0, прямая будет параллельна оси Ox;

При B=0, прямая будет параллельна оси Oy;

При C=0, прямая будет проходить через начало координат;

При A=C=0, при B не= 0, прямая совпадает с осью Ox; при B=C=0, А не= 0, с осью Oy.

Взаимное расположение двух прямых:

Параллельны и совпадают, если A/A1 = B/B1 = C/C1,

Параллельны и не совпадают, если A/A1 = B/B1 не= C/C1,

Пересекаются, если A/A1 не= B/B1.

23) Прямая на плоскости: векторное уравнение прямой; параметрические уравнения прямой; каноническое уравнение прямой; уравнение прямой, проходящей через две точки; взаимное расположение двух прямых, заданных каноническими уравнениями.

r = r0 + st - векторное уравнение прямой.

S (m, n) – направляющий вектор, M0(r0)точка на прямой М0(x0, y0).

Параметрическое уравнение:

{х = х0 + mt

{y= y0 + nt

Выразим t:

x – x0 / m = t и y – y0 / n = t, т.е,

x – x0 / m = y – y0 / n = t – каноническое ур-е прямой.

Уравнение прямой, через две точки.

Условие параллельности - равное соотношение соответствующих величин.

Перпендикулярности – скалярное произведение направляющих векторов = 0.

24) Прямая на плоскости: уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой с угловым коэффициентом; взаимное расположение двух прямых, заданных уравнениями с угловым коэффициентом; расстояние от точки до прямой.

По направлению:

С угловым коэффициентом:

Число называется угловым коэффициентом прямой.

y = kx + b – уравнение прямой с угловым коэффициентом.

b – отрезок, отсекаемы на оси Oy.

Прямые:

Расстояние от точки до прямой:

25) Кривые второго порядка. Эллипс: основные определения; вывод канонического уравнения.

Эллипс – множество точек плоскости, сумма расстояний до которых до двух данных точек плоскости, называемых фокусами – постоянная величина.

отношение фокального расстояния к длине большой оси (эксцентриситет).

Директрисы: (две прямые, перпендикулярные оси Ox, на расстоянии от центра)

26) Кривые второго порядка. Гипербола: основные определения; вывод канонического уравнения.

Гипербола – множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек этой плоскости, называемых фокусами – постоянная величина.

отношение фокального расстояния к длине действительной(фокальной) оси (эксцентриситет).

Директрисы:

Ось, сопряженная с гиперболой:

27) Кривые второго порядка. Парабола: основные определения; вывод канонического уравнения.

Парабола – множество всех точек плоскости, равноудалённых от точки-фокуса и данной прямой, называемой директрисой.

Директриса:

28) Упрощение кривой второго порядка: параллельный перенос системы координат; поворот системы координат.

Параллельный перенос:

Даны две системы координат с одинаковым направлением осей, но разными началами.

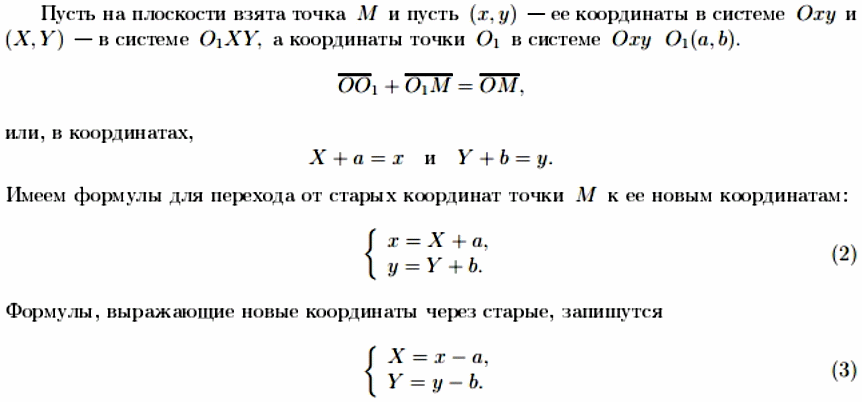
То есть, для нахождения новых координат нужно из старых вычесть соответствующие координаты центра новой системы координат.

Поворот системы координат:

29) Полярная система координат. Вывод полярного уравнения эллипса, гиперболы, параболы.

Вывод полярных уравнений: