1) Матрицы: Основные определения, линейные операции, умножение.

1. Матрица – прямоугольная таблица, размерностью n-строк на m-столбцов.

2. Квадратная матрица – матрица, размер строк и столбцов которой одинаковы.

3. Матрица из одной строки (столбца) называется матрицей-строкой (столбцом).

4. Нулевая матрица – элементы которой – нули.

5. Единичная матрица – квадратная нулевая матрица, с единицами на главной диагонали.

Операции:

• Сумма матриц A и B (одинаковой размерности) – матрица C той же размерности из сумм соответствующих элементов.

• Разность (аналогия сумме).

• Умножение матрицы на число – каждый элемент матрицы умножается на это число.

• Умножение матриц возможно только если количество столбцов первой матрицы равно количеству строк второй. Последовательно перемножаются строки и столбцы.

2) Определители матриц, их свойства (доказать для определителя второго порядка).

Свойства:

1. Определитель транспонированной матрицы равен определителю исходной матрицы

2. Если в определителе какие-либо две строки (столбца) равны между собой, то такой определитель равен нулю.

3. Общий множитель всех элементов какой-либо строки (столбца) можно выносить за знак определителя.

4. Если в определителе поменять поменять местами какие-либо две строки (столбца), то определитель меняет знак.

5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.

6. Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменится.

7. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором – вторые слагаемые.

3) Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)

Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.

Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.

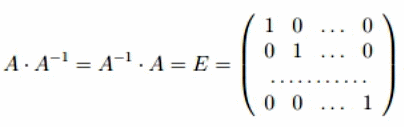
Вырожденной матрицей называется такая матрица, определитель которой равен нулю.

Теорема:

Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.

4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством).

1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A.

2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами.

Т.е. ранг матрицы не изменится если в матрице следующие преобразования: