4. Методы определения оптимальных параметров настройки промышленных регуляторов.
Расчет оптимальных настроек параметров регуляторов по расширенным АФХ
Если кривая разгона объекта далека от типовой , то ошибки могут получиться весьма большие при расчете выше сказанными методами, для этого по имеющейся АФХ объекта строится расширенная АФХ для выбранного значения затухания
Приближенно пар-ры настроек опред-ся след. образом : Кр для П рег-ра числено = обратной величине вектора с углом 180 градусов Кр=1/омега180градусов
Для ПИ рег-ра Кр опред-ся обратной величиной вектора соот-щего углу 150 градусов Кр=1/омега150градусов
Для ПИД рег-ра : Кр=1/омега200градусов*1,2
Время интегрирования Ти :
ПИ : Ти=2/ омега150градусов
ПИД Ти=3,5/ омега200градусов , Тd=(0,15до 0,25)Ти
Расчет оптимальных настроек параметров регуляторов по номограммам
В отличии от формульного м-да, м-д расчета по номограммам позволяет более точно определить настройки рег-ра,т.к учитывает наличие нелинейной зависимости м/у пар-рами настройки рег-ра и величины отношений тау/Т. Номограммы сущ-ют для различных значений степени затухания, для пользования ими необходимо располагать соответствующими расширенными амплитудно-фазовыми хар-ми объекта.
W(jw)=A(jw)*e^iфи(jw)
Желательно при этом, чтобы расширен.АФХ объекта была графически или таблично представлена расширен.ФЧХ в диапазоне от 80-90 до 170-180 градусов и соответветствующим участкам расширен.АЧХ.
Пример :
Рис.25.1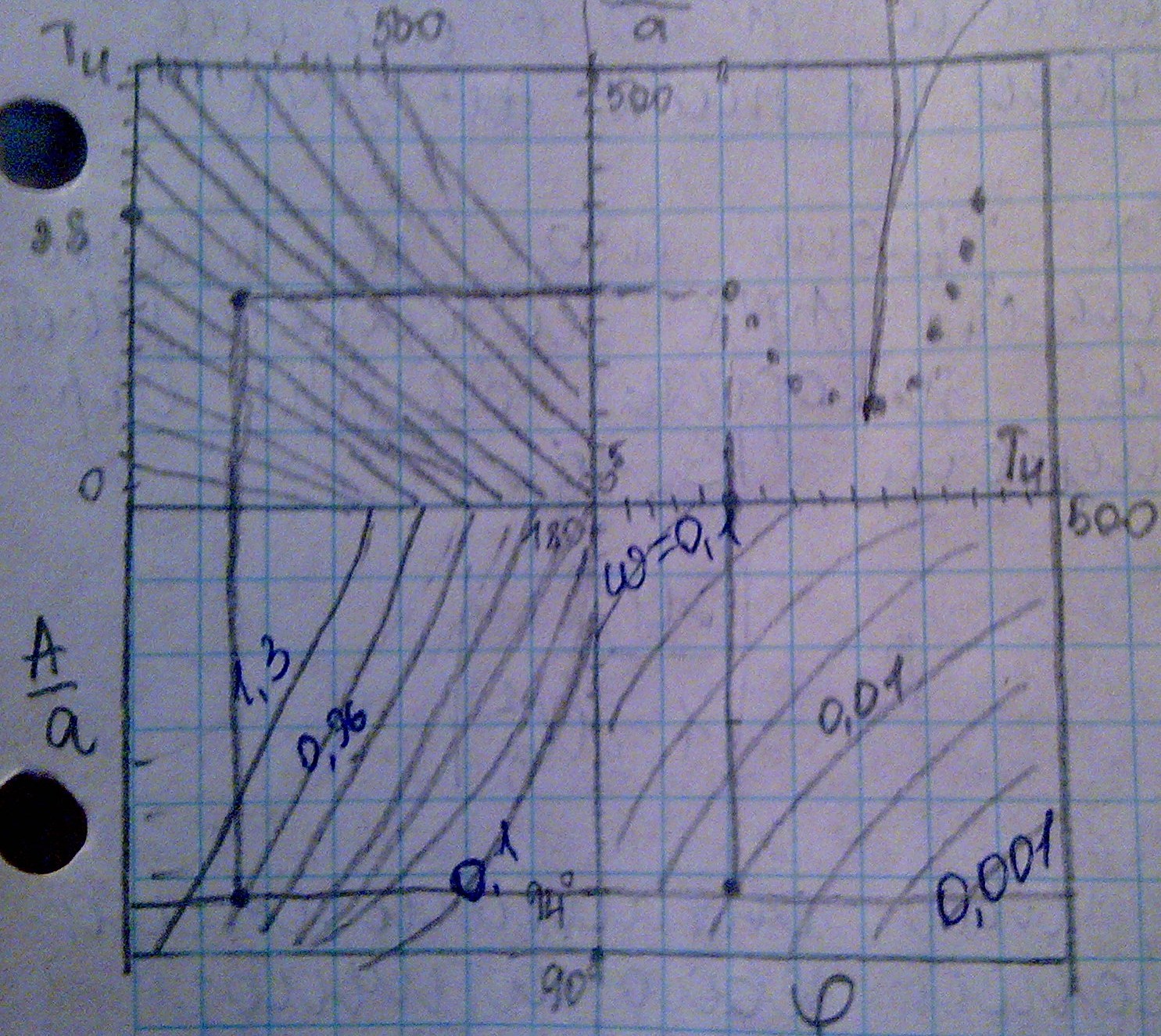
рис.25.2
а-постоян.величина, а[б*/лямда*]. Она должна выбираться из соотношения: Аmax/a<=1, Amin/>0.1 (обычно а=10)
5. Автоколебания в сар. Определение параметров автоколебаний с помощью графических построений.
В нелинейных САР
возможны собственные колебания с
постоянной амплитудой частотой при
отсутствии внешних колебательных
воздействий. Эти колебания могут быть
устойчивыми и неустойчивыми. Устойчивые
собственные колебания с постоянной
амплитудой и частотой при отсутствии
внешних колебательных воздействий
называются автоколебаниями. Удобно
рассматривать эти собственные колебания,
привлекая фазовую плоскость, по осям
которой откладываются координаты х –
отклонение выходной переменной системы
от установившегося значения и
- скорость изменения этого отклонения.
а)
б)
Жирной линией на фазовой плоскости обозначены особые линии – для а) устойчивого, б) неустойчивого предельного циклов.
Предельные циклы
разграничивают области начальных
условий, для которых фазовые траектории
носят качественно разный характер. Так,
для а), фазовые траектории для начальных
условий, находящихся внутри предельного
цикла, раскручиваются от положения
равновесия
до предельного цикла, а для начальных
условий, находящихся вне предельного
цикла, - скручиваются извне до предельного
цикла. Значит, в такой нелинейной системе
нет состояния устойчивого равновесия,
а есть режим автоколебаний. Для случая
б) картина противоположная, здесь для
области начальных условий, расположенных
внутри предельного цикла, имеет место
положение устойчивого равновесия в
начале координат, а предельный цикл
характеризует неустойчивые собственные
колебания.
Если в системе
установились гармонические автоколебания,
то
,
а
,
где А – амплитуда, а ω – частица
гармонических колебаний. Максимальные
значения для х будет при
,
т.е.
;
(1), а для V
при
,
т.е.
.
(2)
На фазовой плоскости
значения амплитуды и частоты автоколебаний
непосредственно не просматриваются.
Однако, их можно определить приблизительно,
исходя из рассмотрения предельного
цикла. Если предельный цикл не является
эталоном, то автоколебания не будут
гармоническими колебаниями. Если,
однако, положить, что автоколебания
будут близки к гармоническим, то из
картинки предельного цикла а) имеем
;
(3)
.
(4) Сравнивая (1) и (3), (2) и (4) имеем для
амплитуды и частоты автоколебаний:
.