
- •Вопросы на гэк 2012
- •1. Нелинейные сар. Понятия: «пространство состояний», «фазовая траектория», «фазовый портрет».
- •2. Проблема двойственности в линейном программировании.
- •3. Составляющие информационной системы (ис). Модели жизненного цикла ис.
- •4. Методы определения оптимальных параметров настройки промышленных регуляторов.
- •5. Автоколебания в сар. Определение параметров автоколебаний с помощью графических построений.
- •6. Математическая постановка задач оптимального управления. Пример: «Нажимное устройство реверсивного прокатного стана».
- •7. Субд. Функции субд. Транзакции. Свойства транзакций.
- •8.20. Оценка качества сар по временным характеристикам
- •9. Представление импульсного элемента при исследовании импульсных сар.
- •10. Синтез сар оптимальной по быстродействию.
- •11. Этапы канонического проектирования информационных систем.
- •12. Принципы системного подхода в моделировании. Сетевые модели.
- •13. Связь между спектрами сигналов на входе и выходе простейшего импульсного элемента. Теорема Котельникова.
- •14. Анализ методов решения задач оптимального управления.
- •15. Модели управления передачей, обработкой и хранением данных в информационных системах на основе технологии «клиент-сервер»
- •16. Непрерывно-стохастические модели на примере систем массового обслуживания.
- •17. Процессы конечной длительности в импульсных сар.
- •18. Метод динамического программирования.
- •19. Составляющие внемашинного информационного обеспечения систем управления. Системы классификации и кодирования информации.
- •21. Алгебраический аналог критерия устойчивости Гурвица для исар.
- •22. Системы управления на основе нечеткой логики.
- •23. Реляционная модель данных. Понятие функциональной зависимости. Процесс нормализации базы данных.
- •Целостность данных
- •Реляционная алгебра
- •Нормализация базы данных
- •Номер преподавателя Группа Сущность Преподаватель - группа
- •24. Синтез сар по логарифмическим характеристикам.
- •25. Метод гармонической линеаризации нелинейностей.
- •26. Системы управления на основе искусственных нейронных сетей.
- •27. Цифровые регуляторы и методы их настроек.
- •28. Аппроксимация кривых разгона методом площадей.
- •29. Характер движения в нелинейных и линейных сар.
- •30. Техническая диагностика. Математические основы технической диагностики.
- •31. Определение оптимальных параметров настройки пи – регуляторов.
- •32. 52. Назначение и функции операционной системы. Классификация и характеристика операционных систем.
- •33. 73. Устойчивость линейных сар. Признаки устойчивости. Запасы устойчивости линейных сар.
- •34. Статистические методы распознавания. Метод Бейеса.
- •35. Определение оптимальных параметров настройки пид – регуляторов.
- •36. Реляционная алгебра Кодда
- •37. Устойчивость линейных непрерывных систем. Критерий устойчивости Найквиста.
- •38. Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент. Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент.
- •Черный ящик
- •39. Определение, назначение и классификация компьютерных сетей. Базовые топологии локальных компьютерных сетей.
- •40. Назначение, классификация и характеристика запоминающих устройств эвм.
- •41. Критерий устойчивости а.М. Ляпунова для нелинейных систем.
- •42. Частотные методы идентификации динамических объектов.
- •43. Определение, назначение и классификация компьютерных сетей. Топология глобальной компьютерной сети.
- •44. Устройства ввода и вывода информации эвм.
- •45. Виды корректирующих средств в сар. Недостатки последовательной коррекции.
- •46. Классификация объектов управления по статическим и динамическим характеристикам.
- •47. Эталонная модель взаимодействия открытых систем osi. Характеристика уровней osi.
- •48. Основные типы регистров и их функции в эвм.
- •49. Гармоническая линеаризация. Физический смысл коэффициентов гармонической линеаризации.
- •50. Идентификация объектов по временным характеристикам. Определение кривой разгона объекта по его импульсной характеристике.
- •51. Программное обеспечение компьютерных сетей.
- •53. Устойчивость нелинейных систем. Метод л.С. Гольдфарба.
- •54. Идентификация динамических систем. Активные и пассивные методы идентификации.
- •55. Характеристика нормальных форм реляционной модели данных.
- •56. Интерфейсы в эвм. Типы и методы взаимодействия устройств вычислительной системы.
- •57. Точные методы исследования устойчивости и автоколебаний в нелинейных системах. Частотный метод в.М. Попова.
- •58. Методы аппроксимации кривых разгона объекта.
- •59. Пользовательские технологии Интернета.
- •60. Архитектура процессора эвм и назначение его функциональных блоков.
- •61. 65. Статические характеристики нелинейных элементов.
- •62. Обеспечивающие подсистемы информационно -управляющих систем и их характеристики.
- •63. Протоколы взаимодействия функциональных блоков компьютерной сети: понятие, виды, иерархия.
- •64. Система прерываний эвм. Механизм обработки прерываний в архитектуре эвм семейства intel.
- •66. 77. Промышленные регуляторы, их назначение и передаточные функции.
- •67. Функциональные подсистемы информационно- управляющих систем и их характеристики.
- •68. Основные принципы построения компьютерных сетей.
- •69. Классификация задач оптимального управления.
- •70. Организационные подсистемы информационно- управляющих систем и их характеристики.
- •71. Подходы к классификации моделей. Обоснование введения моделей. Классификация моделей по способу представления.
- •72. Организация системы ввода-вывода через bios
- •74. Принципы построения автоматизированных систем управления.
- •75. Классификация моделирования. Комбинация видов моделирования при исследовании сложных объектов. Имитационное и компьютерное моделирование.
- •76. Архитектура эвм и назначение основных блоков.
- •78. Состав интегрированной системы автоматизации предприятия.
- •79. Математическая модель и математическое моделирование. Этапы математического моделирования.
- •80. Логические основы проектирования цифровых устройств. Понятие функционально- полного набора логических элементов.
- •Процессы контроля и восстановления информации в эвм. Коды Хемминга: исправление одиночных ошибок, обнаружение двойных ошибок.
- •Виртуальная память и ее реализация. Сегментно-страничная организация памяти и динамическое преобразование адресов. Механизм замещения страниц.
- •Физический смысл коэффициентов гармонической линеаризации.
- •Математические ожидания сигналов на выходе стационарных сар.
- •Классификация систем автоматического регулирования.
- •Понятие и составляющие информационной системы (ис). Модели жизненного цикла ис. Классы задач, решаемые ис.
- •Система моделей предметной области. Функционально-ориентированная модель предметной области.
- •Объектная структура
- •Функциональная структура
- •Структура управления
- •Организационная структура
- •Техническая структура
- •Оперативная аналитическая обработка данных: концепции и технологии.
- •Принципы адресации компьютеров в компьютерной сети.
- •Контроллер прерываний от внешних устройств в архитектуре эвм семейства intel. Программно-аппаратное взаимодействие контроллера прерываний и микропроцессора.
37. Устойчивость линейных непрерывных систем. Критерий устойчивости Найквиста.
Если разомкнутая
САР неустойчива, то среди корней ее
характеристического уравнения
![]() есть т правых
корней. Тогда согласно принципу аргумента
получим
есть т правых
корней. Тогда согласно принципу аргумента
получим

Чтобы замкнутая САР была устойчивой, надо чтобы ее характеристическое уравнение имело бы все корни левые, следовательно, согласно принципу аргумента:
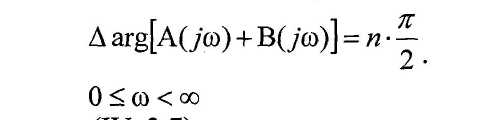 Тогда в этом случае
согласно (IV.
3.7) получим (изменение аргумента
вспомогательного вектора)
Тогда в этом случае
согласно (IV.
3.7) получим (изменение аргумента
вспомогательного вектора)
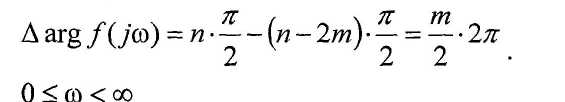
Множитель 2л обозначает, что вектор f(jω) совершает вокруг начала координат полный оборот.
Тогда критерий Найквиста для неустойчивых разомкнутых систем при учете (IV.3. 9) может быть сформулирован следующим образом:
Для устойчивости замкнутой САР при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФХ разомкнутой CAP Wp(jω), начинаясь на действительной оси, при росте частоты ω от 0 до ∞ охватывала точку (-1, j0) в положительном направлении т/2 раз, где т -число правых корней характеристического уравнения разомкнутой САР.
П![]() усть
Wp(jω)
имеет вид, изображенный на рис. IV.1.6,
охватывает точку (-1,j0)
в положительном направлении 1 раз, т.е.
, поэтому m=2.
усть
Wp(jω)
имеет вид, изображенный на рис. IV.1.6,
охватывает точку (-1,j0)
в положительном направлении 1 раз, т.е.
, поэтому m=2.
Е сли
характеристическое уравнение разомкнутой
САР имеет 2 правых корня, система в
замкнутом состоянии устойчива. Для
Wp(jω),
изображенной
на рис. IV.16,
наличие у характеристического уравнения
разомкнутой системы числа правых корней
не равных 2, означает неустойчивость
замкнутой САР.
сли
характеристическое уравнение разомкнутой
САР имеет 2 правых корня, система в
замкнутом состоянии устойчива. Для
Wp(jω),
изображенной
на рис. IV.16,
наличие у характеристического уравнения
разомкнутой системы числа правых корней
не равных 2, означает неустойчивость
замкнутой САР.
Ч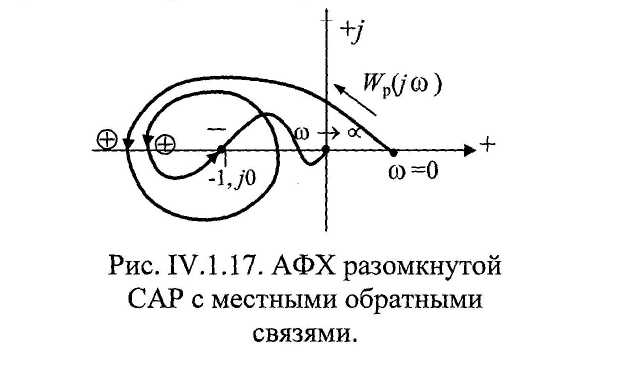 асто
из-за наличия местных обратных связей
АФХ разомкнутой САР совершает несколько
оборотов вокруг точки (-1,j0)
и имеет достаточно замкнутую конфигурацию
(рис. IV.17).
асто
из-за наличия местных обратных связей
АФХ разомкнутой САР совершает несколько
оборотов вокруг точки (-1,j0)
и имеет достаточно замкнутую конфигурацию
(рис. IV.17).
Здесь подсчитывать число оборотов Wp(jω) вокруг точки (-1, j0) затруднительно. Для подобных случаев видный советский ученый Я. 3. Цыпкин предложил удобную методику, базирующуюся на понятиях положительного и отрицательного переходов.
Переход амплитудно-фазовой характеристикой разомкнутой CAP Wp(jω) ростом частоты отрезка действительной оси (-∞;-1] сверху вниз называется
положительным (+), а снизу в верх - отрицательным (-).
Т![]() огда
критерий Найквиста в формулировке
Цыпкина предстает в следующем виде:
Замкнутая САР устойчива, если разность
между числом положительных и отрицательных
переходов равна , где т
- число правых
корней характеристического уравнения
разомкнутой системы.
огда
критерий Найквиста в формулировке
Цыпкина предстает в следующем виде:
Замкнутая САР устойчива, если разность
между числом положительных и отрицательных
переходов равна , где т
- число правых
корней характеристического уравнения
разомкнутой системы.
На рис. IV.17
изображен случай, когда имеется два
положительных и один отрицательный
переход, т.е.
![]()
и, значит, если характеристическое уравнение разомкнутой САР имеет 2 правых корня (только в этом случае!), то замкнутая САР устойчива. Подчеркнем еще раз, что при подсчете переходов исследуется только тот участок (-∞;-1] и не принимается во внимание остальная часть действительной оси.
Сейчас мы рассмотрим случай IV. 3. 3. 2 для неустойчивой разомкнутой САР. Однако, вышеприведенная формулировка Цыпкина критерия Найквиста применима к случаю IV.3. 3. 1, т. е. для устойчивой разомкнутой САР (рис. IV. 18).
 На
рисунке изображена АФХ разомкнутой
системы, имеющая 1 положительный и 1
отрицательный переходы. По Цыпкину
На
рисунке изображена АФХ разомкнутой
системы, имеющая 1 положительный и 1
отрицательный переходы. По Цыпкину![]()
таким образом, система будет устойчива, если разомкнутая система тоже устойчива, т.е. имеет т=0 правых корней своего характеристического уравнения, а это и есть случай IV. 3.3.1.
