22. Системы управления на основе нечеткой логики.

Наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в интеллектуальных компьютерных системах представляют сегодня одно из самых перспективных направлений развития современной вычислительной техники.

Значительный вклад в это направление внес Л. Заде. Его работа «Fuzzy Sets» явилась толчком к развитию новой математической теории. Заде расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0, 1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода. Введя затем понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Заде предложил аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений. Это позволило создать фундамент теории нечетких множеств и нечеткой логики, а также предпосылки для внедрения методов нечеткого управления в инженерную практику. Смещение центра исследований нечетких систем в сторону практических приложений привело к постановке целого ряда проблем таких, как новые архитектуры компьютеров для нечетких вычислений, элементная база нечетких компьютеров и контроллеров, инструментальные средства разработки, инженерные методы расчета и разработки нечетких систем управления и многое другое. Математическая теория нечетких множеств позволяет описать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Нечеткое управление оказывается особенно полезным, когда исследуемые процессы являются слишком сложными для анализа с помощью общепринятых методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Нечеткая логика, предоставляющая эффективные средства отображения неопределенностей и неточностей реального мира, и на которой основано нечеткое управление, ближе к человеческому мышлению и естественным языкам, чем традиционные логические системы.

Нечеткое управление (Fuzzy Control, Fuzzy-управление) в настоящее время является одной из перспективнейших интеллектуальных технологий, позволяющих создавать высококачественные СУ.

Среди причин распространение Fuzzy-управления обычно выделяют следующие:

1. Особые качества СУ с нечеткой логикой, в частности малая чувствительность к изменению параметров ОУ.

2. Синтез СУ с нечеткой логикой при применении современных средств аппаратной и программной поддержки зачастую проще, чем традиционных.

Существуют также и нетехнические причины популярности нечетких систем:

1. Нечеткая логика – технология, появившаяся относительно недавно, и ее применение без труда позволяет достигнуть «патентной чистоты» проектируемых изделий.

2. Существует определенная «мода» на нечеткие системы.

Как и у любых СУ, у систем с нечеткой логикой существует область, в которой их применение является наиболее предпочтительным. В качестве таких областей обычно выделяют следующие:

1. Системы регулирования, для которых модель ОУ определена лишь качественно.

2. Надстройка над традиционными системами регулирования (например, над ПИД-регуляторами) для придания им адаптивных свойств.

3. Воспроизведение действий человека-оператора.

4. Системы организационного управления верхнего уровня.

Общей предпосылкой для применения нечетких СУ является, с одной стороны, наличие неопределенности, связанной как с отсутствием информации, так и сложностью системы и невозможностью или нецелесообразностью ее описания традиционными методами и, с другой стороны, наличие об объекте, необходимых управляющих воздействий, возмущениях и т.п. информации качественного характера.

Т

Рис. 1. Области эффективного применения различных СУ

радиционные методы управления хорошо зарекомендовали себя при относительно невысокой сложности ОУ и наличии достаточно полной информации о нем. Нейросетевые системы управления целесообразно применять при отсутствии информации или при высокой сложности ОУ. Промежуточное положение между данными технологиями занимают нечеткие системы. На рис. 1. показаны области эффективного применения традиционных, нейросетевых и нечетких СУ.

О сновным признаком классификации нечетких СУ является место нахождения блоков нечеткого логического вывода в СУ: либо нечеткая система сама формирует управляющие сигналы, либо сигналы с нечеткой системы управляют параметрами традиционной СУ (например, ПИД-контроллером). К последним также относятся системы с так называемыми нечеткими комплексными моделями (либо плавный, либо скачкообразный) происходит посредством сигналов с блоков нечеткого вывода.

СУ с нечеткой логикой можно разделить также на неадаптивные и адаптивные. В неадаптивных база знаний после подстраивается в процессе работы в зависимости от складывающейся в процессе управления ситуации. При адаптивном подходе к построению нечетких СУ настройка блоков нечеткого логического вывода осуществляется не только в процессе проектирования, но и во время нормальной эксплуатации системы, параллельно с процессом управления объектом. Адаптивные системы позволяют осуществлять более качественное управление сложными нестационарными объектами по сравнению с обычными системами.

Независимо от того, адаптивной или нет является нечеткая СУ, основным вопросом при ее проектировании является формирование базы знаний в виде нечетки продукционных правил.

Три наиболее известных подхода к построению нечетких адаптивных СУ – это инверсное управление, предикатное управление (управление с предсказанием), схема управления с обратной связью и идентификатором.

Примеры СУ с нечеткое логикой

1. Нечеткий регулятор

Р

Рис. 2. Структура замкнутой системы управления

ассмотрим замкнутую систему регулирования, представленную на рис. 2, где через О обозначен объект управления, через Р — регулятор а через и у, е, х — соответственно, входной сигнал системы, ее выходной сигнал, сигнал ошибки (рассогласования), поступающий на вход регулятора, и выходной сигнал регулятора. В рассматриваемой системе регулятор вырабатывает управляющий сигнал х в соответствии с выбранным алгоритмом регулирования например, пропорционально сигналу ошибки, либо ее интегралу и т.п. Предположим что функции регулятора выполняет микроконтроллер, при этом аналоговый сигнал е ограничен диапазоном [-1, 1] и преобразуется в цифровую форму аналого-цифровым преобразователем (АЦП) с дискретностью 0,25, а выходной сигнал регулятора х формируется с помощью цифро-аналогового преобразователя и имеет всего 5 уровней: -1, -0,5; 0, 0,5; 1. Принимая во внимание данные уровни, введем лингвистические переменные: А1: большой положительный, А2: малый положительный, А3: нулевой, А4 малый отрицательный А5: большой отрицательный,

и на дискретном множестве возможных значений сигнала рассогласования е определим функцию принадлежности так, как это приведено в табл. 1.

	-1	-0,75	-0,5	-0,25	0	0,25	0,5	0,75	1
А1(е)	0	0	0	0	0	0	0,3	0,7	1
А2(е)	0	0	0	0	0,3	0,7	1	0,7	0,3
А3(е)	0	0	0,3	0,7	1	0,7	0,3	0	0
А4(е)	0,3	0,7	1	0,7	0,3	0	0	0	0
А5(е)	1	0,7	0,3	0	0	0	0	0	0

Предположим далее, что функционирование регулятора определяется следующими правилами (надо сказать типичными для задачи управления):

П₁: если е = А_з и Δе = Аз, то х = 0, П₂: если е = А₂ и Δе = А₂, то х = -0,5, П₃: если е = А₄ и Δе = А₄, то х = 1, П₄: если е = А₁ и Δе=А₁, то х = -1,

где Δе - первая разность сигнала ошибки в текущий дискретны момент времени.

Заметим, что набор правил может быть, вообще говоря, и каким-то другм. Если например, используется упрощенный алгоритм нечеткого вывода, то при значениях, скажем е = -0,25 и Δе = 0,5 имеем

α1= min(0,7; 0,3)=0,3 и х1=0

α2 = min(0,7; 1)=0,7 и х2= - 0,5

α 3 =min(0; 0,)=0 и х3=1

α4= min(0; 0,3)=0,3 и х4= -1

и выход регулятора

Аналогичным образом значения выходного сигнала регулятор рассчитываются при других значениях е и Δе.

Отметим, что при проектировании подобных («нечетких») регуляторов основным (и не формализуемым) этапом является задания набора нечетких правил. Другие аспекты: выбор формы функций принадлежности, алгоритма приведения к четкости и т. п. представляются задачами более простыми.

Моделирование работы светофора на основе нечеткой логики

В обычном светофоре время работы зеленого и красного света, а также время цикла фиксированы. Это создает некоторые трудности в движении машин, особенно, при изменении их потоков в часы пик, что довольно часто приводит к появлению автомобильных пробок.

В предлагаемом нечетком светофоре время цикла остается постоянным, однако, время его работы в режиме зеленого света должно меняться в зависимости от количества подъезжающих к перекрестку машин.

П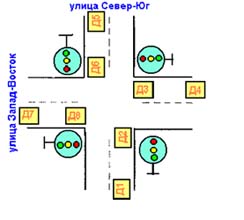 усть время цикла традиционного и нечеткого светофоров будет одинаковым и равным 1мин.=60сек. Длительность зеленого света обычного светофора зададим 30сек., тогда красный свет будет гореть тоже 30сек.

Для работы нечеткого светофора на перекрестке улиц Север-Юг (СЮ) и Запад-Восток (ЗВ) необходимо установить 8 датчиков (рис.1), которые считают проехавшие мимо них машины.

Рис.1. Расположение датчиков на перекрестке.

Светофор использует разности показаний четырех пар датчиков: (Д1-Д2), (Д3-Д4), (Д5-Д6) и (Д7-Д8). Таким образом, если для улицы СЮ горит зеленый свет, машины проезжают перекресток и показания двух пар датчиков равны: Д1=Д2, Д5=Д6, а, следовательно, их разность равна нулю. В это же время на улице ЗВ перед светофором останавливаются машины, которые успели проехать только Д4 и Д7. В результате можно рассчитать суммарное количество автомобилей на этой улице следующим образом: (Д4-Д3)+(Д7-Д8)=(Д4-0)+(Д7-0)=Д4+Д7.

Для сравнения работы обоих светофоров введем показатель эффективности, в качестве которого будем рассматривать число машин, не проехавших перекресток за один цикл светофора.

Данную задачу можно сравнить с системой массового обслуживания (СМО), по двум каналам которой поступают заявки на обслуживание в виде автомашин. Показатель эффективности в этом случае число заявок, получивших отказ.

РЕШЕНИЕ :

Более подробно рассмотрим проектирование нечеткой подпрограммы. Здесь однозначно должны быть определены все входы и выходы.

Поскольку работа светофора зависит от числа машин на обеих улицах и текущего времени зеленого света, для нашей подпрограммы предлагается использовать 3 входа: число машин на улице СЮ по окончанию очередного цикла, число машин на улице ЗВ по окончанию цикла и время зеленого света нечеткого светофора.

Т еперь для каждой переменной надо задать лингвистические термы, соответствующие некоторым диапазонам четких значений. Так, для переменной время зеленого света предлагается использовать три терма (рис.2):

Рис.2. Функция принадлежности

• малое (10-25сек.);

• среднее(20-40сек.); первой входной переменной

• б ольшое(35-50сек.).

Степень принадлежности четких значений термам задается с помощью функций принадлежности (в нашем случае эти функции имеют форму трапеции).

Аналогично, термы для двух оставшихся переменных будут (рис.3):

• очень малое (0-18);

• малое (16-36);

• с реднее (34-56);

• большое (54-76);

• очень большое (72-90).

Рис.3. Функция принадлежности второй и третьей входных переменных.

Функции принадлежности здесь также имеют форму трапеции.

Так как суть работы светофора состоит в изменении времени зеленого света, в качестве выходного параметра предлагается использовать величину этого изменения. Термы в этом случае будут следующие (рис.4):

• уменьшить (-20-0сек.);

• не изменять (-15-15сек.);

• увеличить (0-20сек.).

Рис.4. Функция принадлежности выходной переменной.

Функции принадлежности имеют форму Гаусса.

Кроме того, в подпрограмму записывается таблица правил на основе условных высказываний, которая формирует выходное значение исходя из величин входных параметров, например: Если (число машин на улице СЮ=малое)&(число машин на улице ЗВ=большое)&(время зеленого света на улице СЮ=большое), то (время зеленого света=уменьшить).