- •Вопрос №1: Множества. Основные понятия. Операции над множествами.
- •Вопрос №2. Основные числовые множества. Некоторые свойства действительных чисел. Геометрическая интерпретация действ чисел. Окрестность точки.
- •Вопрос №3. Ограниченные и неограниченные множества.
- •Вопрос №4: Точные грани числовых множеств. Существование точных граней у ограниченных множеств (с доказательством).
- •Билет №5. Числовые последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- •Вопрос 6. Свойства бесконечно малых и бесконечно больших последовательностей.
- •9.Свойства сходящихся последовательностей: предельный переход в неравенствах.
- •10.Монотонные последовательности. Признак Вейерштрасса сходимости монотонной последовательности.
- •Вопрос 11. Бином Ньютона. Свойство биномальных коэффициентов. Треугольник Паскаля.
- •Вопрос 12. Число е.
- •15. Фундаментальные последовательности. Критерий Коши сходимости последовательности.
- •1 Способ. (с помощью опр. По Гейне)
- •2 Способ. (с помощью опр. Предела по Коши)
- •Обобщение предела функции в точке. Предел функции при х . Односторонние пределы функции.
- •8.2. Предел функции при х
- •8.3 Односторонние пределы функции
- •Вопрос 19.
- •Вопрос 21. Бесконечно малые и бесконечно большие функции.
- •Вопрос 22. Непрерывность функции в точке. Примеры непрерывных точек.
- •2) Конечный или бесконечный ;
- •Вопрос 33. Сравнение функций. Символика o и o.
1 Способ. (с помощью опр. По Гейне)
Т.к.
x->a,
то рассмотрим произв. Послед.
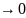 ,при
n
,при
n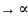 такую, что
такую, что
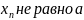
Используя
свойства предела посл-ти получим
=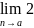 -3*
-3*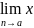 =2-3x
=2-3x
2 Способ. (с помощью опр. Предела по Коши)
Требуется
для любого Эпсилон >0 найти число
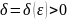 такое, что для всех х, удовл. условию
0<|x-a|<
,
выполнялось бы нер-во |(2-3x)(2-3x)|<
3|x-a|<
|x-a|<
такое, что для всех х, удовл. условию
0<|x-a|<
,
выполнялось бы нер-во |(2-3x)(2-3x)|<
3|x-a|<
|x-a|<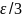 .
Очевидно, что достаточно взять f(
.
Очевидно, что достаточно взять f(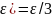
Обобщение предела функции в точке. Предел функции при х . Односторонние пределы функции.
8.2. Предел функции при х
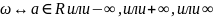
Определение предела функции в точки по Кошизаписывается в терминах окрестностей и позволяет поместить его беск. отдоления точек.
Определение 1.
(Число А
называется пределом функции f(x)
при х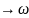 )
(
)
(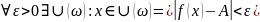
Замечание:
1) В опре. Содержится требование, чтобы область определения функции содержала некот. Окрестность точки
2) Заменяя условие
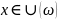 соответствующим неравенством, получим
определение по Коши для случаев х
соответствующим неравенством, получим
определение по Коши для случаев х
3) Используя б.б.п.
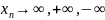 легко сформулировать опр. Предела по
Гейне для этих же случаев.
легко сформулировать опр. Предела по
Гейне для этих же случаев.
4) Как и в случае х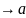 ,
где а
,
определения пределов по Коши и по Гейне
эквивалентны
,
где а
,
определения пределов по Коши и по Гейне
эквивалентны
8.3 Односторонние пределы функции
Определение 1. (по Гейне)
Число А
называется левым пределом f(x)
в точке А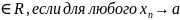 сходится посл-ти элементы которой меньше
левого (больше правее), и выполняется
неравенство
сходится посл-ти элементы которой меньше
левого (больше правее), и выполняется
неравенство
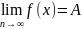
Определение 2.
Число А
называется левым (правым) пределом f(x)
в точке А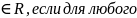
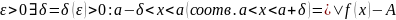 |<
|<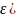
Замечание:
Опр. Односторонних
пределов по Коши легко формулируются
в терминах полуокрестностей точки
а:
)(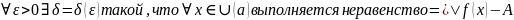 |<
|<
Теорема. (Определения по Коши и по Гейне эквивалентны)
Док-во: аналогично.
Теорема. (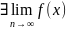 )(1.
)(1.
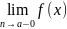 и
и
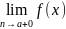 2.
=
)
2.
=
)
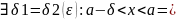 |
|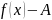 |<
|<
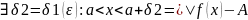 |<
|<
Вопрос 19.
Свойства пределов функций, связанные с арифметическими операциями и предельным переходом в неравенства.
Теорема 1
]
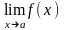 =A
и
=A
и
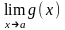 =B
=B
Тогда
1).
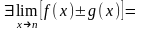 А
А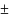 В
В
2.
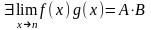
3.
при
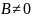
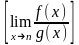 =
=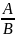
Докажем 2е определение по Гейне
]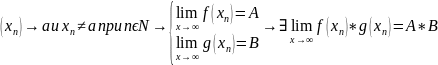
ЧТД!!!
Теорема 2.
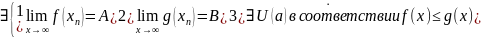
Док-во
Рассмотрим
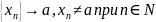 все ее члены лежат в проколотой окресности
все ее члены лежат в проколотой окресности
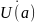
Тогда
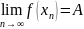
И
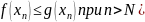
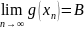
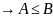
ЧТД!!!
Теорема 3(о промежуточных значения, правило о двух Милиционерах)
]
1)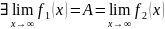
2)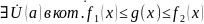
Тогда
1)
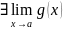
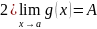
Док-во
]
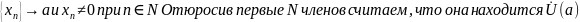
Тогда
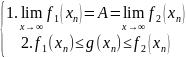
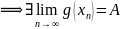
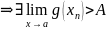
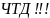
Билет 20
Локальная ограниченность функции, имеющих конечный предел. Критерий Коши существования конечного предела.
Теорема 1. Локальная ограниченность.
]
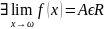
Тогда
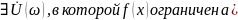
Док-во:
В определении
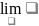 по Коши возьмем
по Коши возьмем
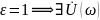 , В которой
, В которой
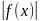 =
=
ЧТД!!!
Определение.(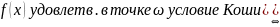 (Для
(Для
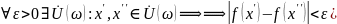
Замечание! В определении содержится требование ,чтобв D(f) содержала некоторую проколотую окрестность точки
Теорема 2. Критерий Коши существ предела функции.
Для
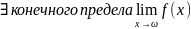 необходимо
и достаточно, чтобы
необходимо
и достаточно, чтобы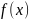 удовлетворяла условию в т.
условия Коши
удовлетворяла условию в т.
условия Коши
Док-во:
Необх.
Для
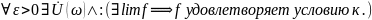 .
.
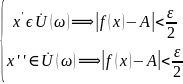
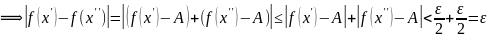 ,
если
,
если

ЧТД!!!
Вопрос 21. Бесконечно малые и бесконечно большие функции.
Определение
1: функция
f(x)
называется бесконечно малой функцией
в точке ω, если
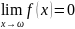 .
.
Пример:
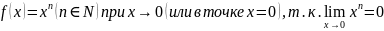
Замечание: в определении (в скрытом виде) содержится требование, чтобы область определения D(f) содержала некоторую проколотую окрестность точки ω.
Определение
2: функция
f(x)
называется бесконечно большой функцией
в точке ω, если для
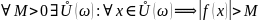
Кроме
того, если в некоторой Ů(ω)
f(x)
≥ 0, то пишут
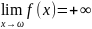 ,
а если f(x)<0,
то
,
а если f(x)<0,
то
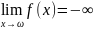
Замечание:
определения конечного и бесконечного
пределов в терминах окрестностей имеют
одинаковый вид. Пусть Ω – либо
действительное число A,
либо один из символов: ∞, +∞ или -∞.
Тогда:
проколотая окрестность U(ω),
в которой справедлива принадлежность
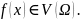
Теорема:
если α(x)
- бесконечно малая функция при xω
и
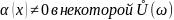 ,
то
,
то
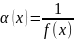 – бесконечно малая функция при xω.
– бесконечно малая функция при xω.
Доказательство:
с помощью последовательностей