
- •Вопрос №1: Множества. Основные понятия. Операции над множествами.
- •Вопрос №2. Основные числовые множества. Некоторые свойства действительных чисел. Геометрическая интерпретация действ чисел. Окрестность точки.
- •Вопрос №3. Ограниченные и неограниченные множества.
- •Вопрос №4: Точные грани числовых множеств. Существование точных граней у ограниченных множеств (с доказательством).
- •Билет №5. Числовые последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- •Вопрос 6. Свойства бесконечно малых и бесконечно больших последовательностей.
- •9.Свойства сходящихся последовательностей: предельный переход в неравенствах.
- •10.Монотонные последовательности. Признак Вейерштрасса сходимости монотонной последовательности.
- •Вопрос 11. Бином Ньютона. Свойство биномальных коэффициентов. Треугольник Паскаля.
- •Вопрос 12. Число е.
- •15. Фундаментальные последовательности. Критерий Коши сходимости последовательности.
- •1 Способ. (с помощью опр. По Гейне)
- •2 Способ. (с помощью опр. Предела по Коши)
- •Обобщение предела функции в точке. Предел функции при х . Односторонние пределы функции.
- •8.2. Предел функции при х
- •8.3 Односторонние пределы функции
- •Вопрос 19.
- •Вопрос 21. Бесконечно малые и бесконечно большие функции.
- •Вопрос 22. Непрерывность функции в точке. Примеры непрерывных точек.
- •2) Конечный или бесконечный ;
- •Вопрос 33. Сравнение функций. Символика o и o.
Билет №5. Числовые последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
Пусть
любому
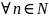 поставим в соответствие числа
поставим в соответствие числа
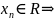 x1,
x2,…,xn
(элементы последовательности) – числовая
последовательность.
x1,
x2,…,xn
(элементы последовательности) – числовая
последовательность.
Примеры:
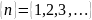
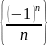 =
=
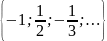
Замечание:
xn
и xm
при
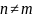 – считаются разными членами
последовательности, хотя как числа
могут совпадать.
– считаются разными членами
последовательности, хотя как числа
могут совпадать.
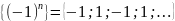
Определение: Пусть { Хn} и {Уn} – числовые последовательности тогда:
{Xn+Yn} – сумма
{Xn-Yn} – разность
{Xn*Yn} – произведение
{Xn/Yn}(yn 0) – частное
Определение:
Последовательность
{Xn}
называется ограниченной сверху, если
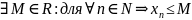 .
.
Определение:
Последовательность
{Xn}
называется ограниченной снизу, если
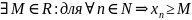 .
.
Определение:
Последовательность
{Xn}
называется ограниченной, если
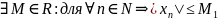
Определение:
Последовательность
{Xn}
называется ограниченной, если
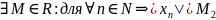
Пример:
1.
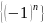 – не ограничена;
– не ограничена;
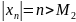 при
при
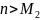
2.
– ограниченнная;
 для
для
Определение 1:
Последовательность
{αn}
называется бесконечно малой (б.м.п.),
если для
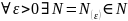 :
для
:
для
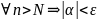
Замечание:
очевидно что
Опр.1 можно записать в следующем виде:
для
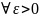 лишь конечное
число членов этой последовательности
удовлетворяет неравенству|αn|>=ε.
лишь конечное
число членов этой последовательности
удовлетворяет неравенству|αn|>=ε.
Определение
2: ({Xn}
– б.м.п.)
(Для
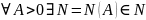 :
для
:
для
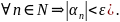
Замечание:
Эквивалентная
формулировка опр.2: Для любого А
0
лишь конечное число последовательности
удовлетворяет неравенству
хn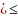 A.
A.
Примеры:
1.
-б.м.п.
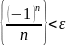 при n
N
(
при n
N
(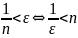 )
)
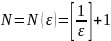
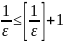
2.
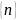 ,
,
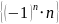 ,
,
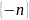 – б.б.п.
– б.б.п.
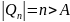 при n
при n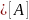
Замечание:
1. Любая б.б.п. является неограниченной
2. Обратное вообще говоря неверно
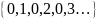 – неограниченно,
но не б.б.п.
– неограниченно,
но не б.б.п.
Вопрос 6. Свойства бесконечно малых и бесконечно больших последовательностей.
Лемма 1. Б.м.п. – ограничена.
Доказательство:
Пусть
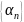 б.м.п. Возьмём
б.м.п. Возьмём
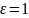 в определение для бесконечно малых
последовательностей
в определение для бесконечно малых
последовательностей
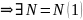 :
для
:
для
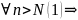
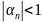
М=max
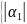 ,
,

М=max
,…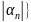 + 1
+ 1
Лемма 2.
1)
Если
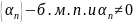 для
,
то
для
,
то
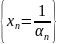 – б.б.п.
– б.б.п.
2)
Если
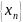 – б.б.п. и
– б.б.п. и
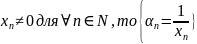 – б.м.п.
– б.м.п.
Доказательство:
1)
Пусть А – произвольное положительное
число
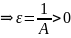 подставим
в определение б.м.п. для
подставим
в определение б.м.п. для
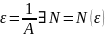 :
Для
:
Для
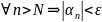
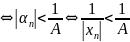
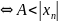 при
при
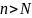
2)
Фиксируем произвольную
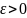 А=
А=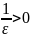 подставляем в определение 2 для А=
подставляем в определение 2 для А=
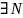 =
=
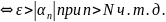
Лемма 3
1)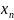 – б.м.п.
– б.м.п.
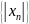 –б.м.п.
–б.м.п.
2)
сумма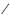 разность
2-х б.м.п. = б.м.п.
разность
2-х б.м.п. = б.м.п.
Доказательство:
1)
Определение того, что
и последовательность из модуля
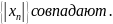
2)
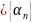 и
и
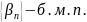
Для
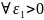
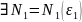 :
:
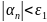
Для
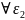
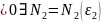 :
:
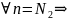
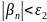
Фиксируем
произвольно
и положим
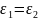 =
=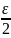 и
и
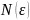 =max
=max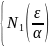 ,
,
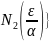
Очевидно, что при n N выполняется неравенство:
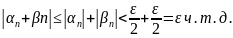
Следствие: Алгебраическая сумма любого конечного числа б.м.п. – б.м.п.
Доказательство: методом математической индукции.
Лемма 4. Произведение ограниченной последовательности и б.м.п.= б.м.п.
Доказательство:
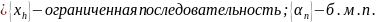
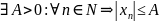
Для
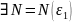 :
для
:
для
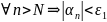
Фиксируем
произвольно
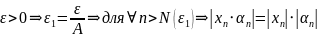 =
=
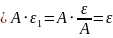 ч.т.д.
ч.т.д.
Следствие 1 Произведение 2-х б.м.п.=б.м.п.
Доказательство: б.м.п. по Лемме 1 можно взять за ограниченную.
Следствие 2 Произведение любого количества б.м.п.= б.м.п.
Доказательство: методом математической индукции.
Лемма5.
Если
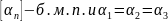 =
…
=
…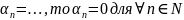
Доказательство:
Для
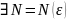 :
для
:
для
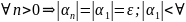 положительного
числа.
положительного
числа.
Предел числовой последовательности. Единственность предела. Ограниченность сходящейся последовательности.
Определение:
последовательность
{xn}
называют сходящейся, если
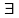
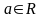 такое,
что последовательность { xn
- a}
- бесконечно малая последовательность.
В этом случае говорят что последовательность
{xn}
сходится (к числу а), или имеет предел,
который равен а.
такое,
что последовательность { xn
- a}
- бесконечно малая последовательность.
В этом случае говорят что последовательность
{xn}
сходится (к числу а), или имеет предел,
который равен а.
(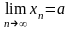 )
или (xn→a
при n→∞)
)
или (xn→a
при n→∞)
На «έ - языке»:
(
)
Для
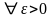
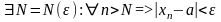
Замечание:
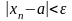
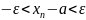
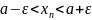

В терминах окрестностей: (У МЕНЯ В КОНСПЕКТЕ НЕТ, в ПДФ СИМУШЕВА ЭТОГО ТОЖЕ НЕТ)
П ример:
Доказать, что
ример:
Доказать, что
Замечание:
1)
согласно определению
(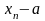 )
– бесконечно малая последовательность
=>
)
– бесконечно малая последовательность
=>
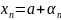 (a
+ альфа энное).
(a
+ альфа энное).
2) Добавление или отбрасывание у последовательности любого конечного числа членов не влияет на существование предела последовательности и его величину.
Теорема 1: сходящаяся последовательность {xn} имеет единственный предел.
Доказательство: пусть и b≠a. Докажем, что b не может быть пределом. Возьмём
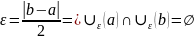 ;
;
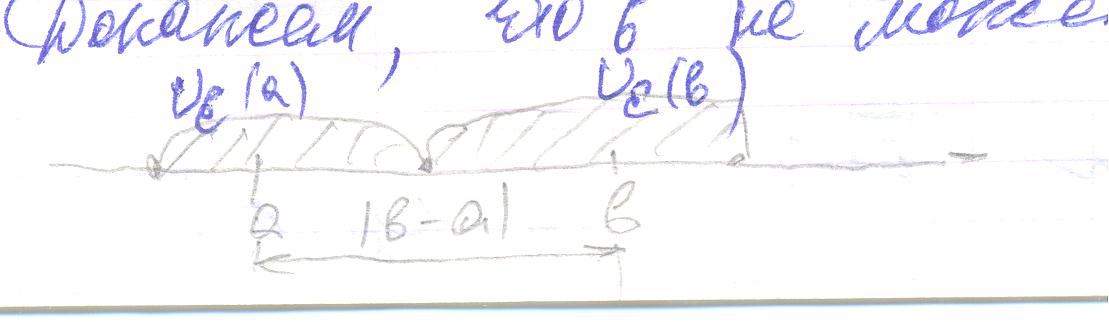 для
для
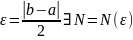 ;
;
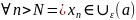 .
.
Вне
этой окрестности может лежать лишь
конечное число членов этой последовательности,
поэтому в
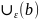 может лежать лишь конечное число членов,
отсюда b
не является пределом.
может лежать лишь конечное число членов,
отсюда b
не является пределом.
Теорема 3: сходящаяся последовательность ограничена.
Доказательство:
фиксируем
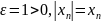
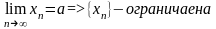
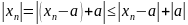
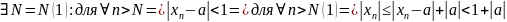
M=max
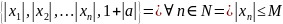 .
.
З амечание:
не всякая ограниченная последовательность
сходится.
амечание:
не всякая ограниченная последовательность
сходится.
Предел числовой последовательности. Единственность предела. Ограниченность сходящейся последовательности.
Определение:
функцию
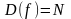 называют
числовой последовательностью.
называют
числовой последовательностью.
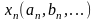 -
члены числовой последовательности.
-
члены числовой последовательности.
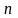 -
номер члена числовой последовательности.
-
номер члена числовой последовательности.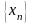 или
или
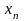 ,
,
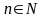 =
=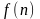 ,
-общий
член.
,
-общий
член.
Определение:
Число
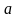 называется пределом последовательности
называется пределом последовательности
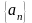 (пишут
(пишут
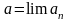 ),
если для любого положительного числа
),
если для любого положительного числа
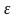 (
>0)
можно указать такое число
(
>0)
можно указать такое число
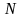 ,
зависящее от
,
что
,
зависящее от
,
что
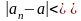 для всех
для всех
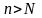 .
.
Теорема: (о единственности предела): Если -сходящаяся, то предел единственный.
Д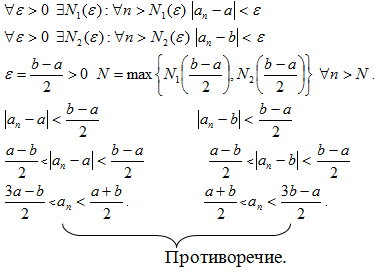 оказательство:
оказательство:
Пусть
,
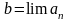 ,
,
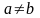 .
.
Для
определенности
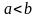 имеем:
имеем:
Теорема: (об ограниченности сходящейся последовательности): Если -сходится, то она ограничена.
-
сходящаяся
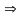
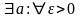
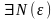 :
:
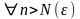 .
.
Возьмем
=1
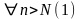
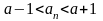 .
.
Обозначим
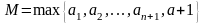 ,
тогда
,
тогда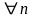
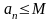
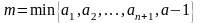 ,
тогда
,
тогда
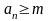
Отсюда
для обоих случаев
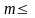
Замечание: обратное не верно.
Свойства пределов, связанные с арифметическими операциями над последовательностями.
Теорема 1: если {xn} и {yn} сходятся, то сходятся последовательности, являющиеся их суммой, разностью и произведением, причём:
1)
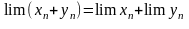
2)
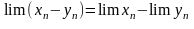
3)
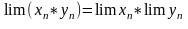
Пусть
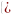 =>
;
где {
=>
;
где {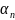 },{
},{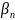 }
– бесконечно малые последовательности.
}
– бесконечно малые последовательности.
1-2)
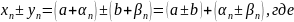
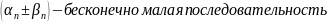
3)
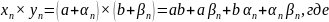
 =>
=>
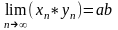 Ч.т.д.
Ч.т.д.
Л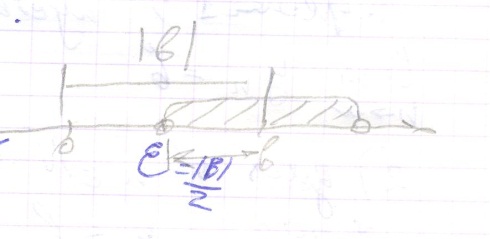 емма:
Пусть {yn}
– сходится, причём
емма:
Пусть {yn}
– сходится, причём
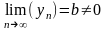 и
и
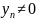 (
(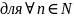 )
)
Тогда
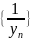 ограничена.
ограничена.
Для
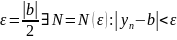
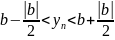 ;
;
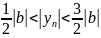 ;
;
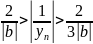 ;
M=max
;
M=max
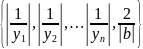
Теорема
2:
если {xn}
и {yn}
сходятся, причём
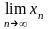 =a
,
=a
,
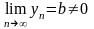 и
и
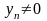 (при n
N),
то
(при n
N),
то
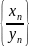 сходится к
сходится к
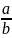 (предел отношения равен отношению
пределов).
(предел отношения равен отношению
пределов).
Доказательство:
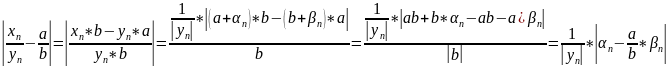 – бесконечно
малая последовательность (
– бесконечно
малая последовательность (
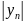 – ограниченная последовательность,
– ограниченная последовательность,
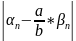 - бесконечно малая)
- бесконечно малая)
Теорема об арифметике пределов последовательностей.
Пусть
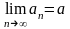 ,
,
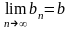 .
Тогда: 1)
существует
.
Тогда: 1)
существует
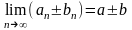 2)
существует
2)
существует
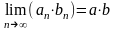
3)
если
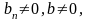 то
существует
то
существует
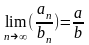 .
.
Доказательства:
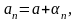
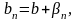 где
где
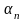 и
и
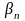 -
бесконечно малые последовательности.
-
бесконечно малые последовательности.
1)
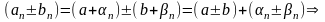
бесконечно малые.
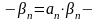 бесконечно
малые.
бесконечно
малые.

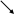 2)
2)
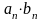 =
=
бесконечно малая бесконечно малая
бесконечно малая
3)
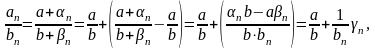 где
где
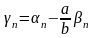 -
бесконечно малая последовательность.
-
бесконечно малая последовательность.
По условию
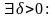
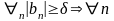
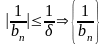 -ограниченная.
-ограниченная.
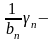 бесконечно
малая.
.
бесконечно
малая.
.
