
- •Вопрос №1: Множества. Основные понятия. Операции над множествами.
- •Вопрос №2. Основные числовые множества. Некоторые свойства действительных чисел. Геометрическая интерпретация действ чисел. Окрестность точки.
- •Вопрос №3. Ограниченные и неограниченные множества.
- •Вопрос №4: Точные грани числовых множеств. Существование точных граней у ограниченных множеств (с доказательством).
- •Билет №5. Числовые последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- •Вопрос 6. Свойства бесконечно малых и бесконечно больших последовательностей.
- •9.Свойства сходящихся последовательностей: предельный переход в неравенствах.
- •10.Монотонные последовательности. Признак Вейерштрасса сходимости монотонной последовательности.
- •Вопрос 11. Бином Ньютона. Свойство биномальных коэффициентов. Треугольник Паскаля.
- •Вопрос 12. Число е.
- •15. Фундаментальные последовательности. Критерий Коши сходимости последовательности.
- •1 Способ. (с помощью опр. По Гейне)
- •2 Способ. (с помощью опр. Предела по Коши)
- •Обобщение предела функции в точке. Предел функции при х . Односторонние пределы функции.
- •8.2. Предел функции при х
- •8.3 Односторонние пределы функции
- •Вопрос 19.
- •Вопрос 21. Бесконечно малые и бесконечно большие функции.
- •Вопрос 22. Непрерывность функции в точке. Примеры непрерывных точек.
- •2) Конечный или бесконечный ;
- •Вопрос 33. Сравнение функций. Символика o и o.
Вопрос №3. Ограниченные и неограниченные множества.
Определение.
Множество А
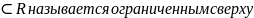 ,
если существует такое М
,
если существует такое М
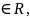 что
для каждого элемента х
А выполняется неравенство х
что
для каждого элемента х
А выполняется неравенство х
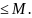 При этом число М называется верхней
гранью множества А.
При этом число М называется верхней
гранью множества А.
(А
ограниченно сверху)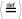 (
(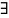 М
М
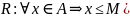
Определение.
Множество А
нвзывается ограниченным снизу, если
существует такое m
,
что для каждого элемента х
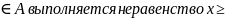 m.При
этом число m
называется нижней гранью множества А.
m.При
этом число m
называется нижней гранью множества А.
(А
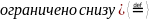 (
(
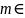
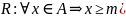 .
.
Определение. Множество А называется ограниченным , если оно ограничено и сверху и снизу.
(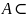
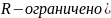 (
(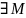 1
1
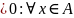
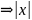
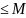 1).
1).
Построим
отрицание утверждения
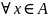
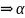 .
.
Если данное утверждение не имеет смысла, то предложение имеет место не для всех х А, то есть существует элемент х А , для которого не имеет места:
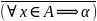 (
х
А
(
х
А
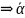 )
)
Аналогично:
 (
(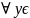 В
В
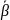 )
)
Правило.
Для построения отрицания данной
логической формулы, содержащей знаки
и
необходимо знак
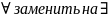 ,
а знак
на
и отрицание (черту) перенести на свойство,
стоящее после стрелки
.
,
а знак
на
и отрицание (черту) перенести на свойство,
стоящее после стрелки
.
Примеры:
1.
(В
- неограничено сверху)
(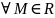
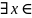 В
В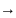 х
М)
х
М)
2.
(С
- неограниченно снизу)
(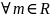
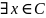 :
х
m)
:
х
m)
3.
(D
- неограниченно)
(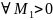
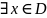 х
х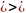 М1)
М1)
4. А = (-∞; b) – ограничено сверху числом b.
5. В = (а; +∞) – ограничено снизу числом а.
6. С = (а; b) – ограничено сверху числом b, а снизу числом а (М1 = max(а ; b)).
7.
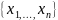 – ограничено множество.
– ограничено множество.
Замечания:
1. Ограниченное сверху множество А имеет бесконечно много верхних граней. Если М - верхняя грань, то и М* М – тоже.
2. Аналогично, ограниченное снизу множество В имеет бесконечно много нижних граней.
Вопрос №4: Точные грани числовых множеств. Существование точных граней у ограниченных множеств (с доказательством).
Точные верхние и нижние грани множеств.
Определение
1.
Пусть множество
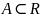 ограничено сверху. В этом случае точной
верхней гранью множества А называется
число Sup
A,
равное наименьшей из всех верхних граней
этого множества.
ограничено сверху. В этом случае точной
верхней гранью множества А называется
число Sup
A,
равное наименьшей из всех верхних граней
этого множества.
Определение
1*
Число
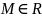 называется точной верхней гранью
ограниченного сверху множества А, если
оно
удовлетворяет следующим 2-м условиям:
называется точной верхней гранью
ограниченного сверху множества А, если
оно
удовлетворяет следующим 2-м условиям:
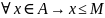 ,
то есть М-верхняя грань множества А
,
то есть М-верхняя грань множества А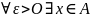 :
:
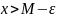 ,
то есть ни одно число, меньшее М не
является верхней гранью множества А.
,
то есть ни одно число, меньшее М не
является верхней гранью множества А.
Теорема. Определение 1 и определение 1* эквивалентны.
Определение
2.
Пусть множество
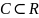 ограничено снизу. В этом случае точной
нижней гранью множества С называется
число inf
C,
равное наибольшей из всех нижних граней
этого множества.
ограничено снизу. В этом случае точной
нижней гранью множества С называется
число inf
C,
равное наибольшей из всех нижних граней
этого множества.
Определение
2*.
Число
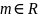 называется точной нижней гранью
ограниченного снизу множества С, если
оно удовлетворяет следующим 2-м условиям:
называется точной нижней гранью
ограниченного снизу множества С, если
оно удовлетворяет следующим 2-м условиям:
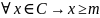 ,
то есть m
– нижняя грань множества С;
,
то есть m
– нижняя грань множества С;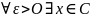
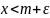 ,
то есть ни одно число, большее m
не является нижней гранью множества
С.
,
то есть ни одно число, большее m
не является нижней гранью множества
С.
Теорема. Определение 2 и 2* эквивалентны.
Примеры:
1. А=(a; b) inf A = a и Sup A = b
2.
С
=
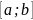 inf C = a и
Sup C = b
inf C = a и
Sup C = b
Определение 3.
Для
неограниченного сверху множества А
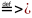 Snp
A
= +
Snp
A
= +
Для неограниченного снизу множества С inf С =-
Теорема.
1) Всякое ограничение сверху непустое множество имеет Sup A .
2)Всякое ограничение снизу непустое множество С имеет inf C .
Доказательство.
Докажем
только 1-ый пункт теоремы. Рассмотрим
множество В, состоящее из всех верхних
граней множества А. Очевидно, что В
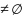 . По свойству непрерывности множества
. По свойству непрерывности множества
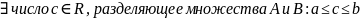 для
для
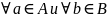 .
Очевидно, что с = Sup
A.
.
Очевидно, что с = Sup
A.
Замечание. Как видно из доказательства теоремы, она выражает важное свойство множества действительных чисел – полноту.
