Вопрос №1: Множества. Основные понятия. Операции над множествами.
Понятия «множество», «элемент» и понятие «принадлежности» являются первичными (исходными) в математике и не определяются через другие более простые понятия. Можно дать лишь некоторые пояснения этих понятий.
Множество – набор, совокупность, собрание каких-либо объектов производной природы, называемых его элементами (синонимы: класс, семейство, набор, система и т.д.).
Обозначение:
множества принято обозначать заглавными
буквами латинского или греческого
алфавитов (A,B…;
,…),
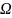а их элементы – малыми буквами тех же
алфавитов (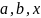
…;
…).
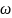Принадлежность
элемента a
к множеству А записывается с помощью
знака принадлежности
:
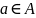(или
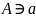– множество А содержит
).
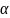Если
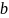не принадлежит B,
то пишут
.
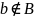Определение
Множество называется подмножеством
множества B
(множество А включено в множество B),
если все элементы множества А принадлежат
множеству B:
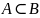(или
)
{
}
{
}.
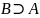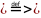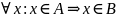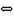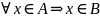Символ
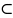называется символом включения.
Замечание. Включение (символ ) и принадлежность (символ ) – разные понятия.
Определение
Множество А равно множеству B
(при этом пишут А=В), если
и
(т.е.
множества А и В состоят из одних и тех
же элементов):
{
}.
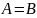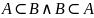Определение Множества, состоящие из конечного числа элементов, называются конечными (например, множество малых букв латинского алфавита).
Определение Множество называется бесконечным, если для любого натурального числа n в этом множестве имеются элементы, количество которых больше n.
Определение
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
символом
.
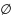Замечание. Пустое множество включено в любое множество.
Способы задания множеств.
10. Перечислением элементов.
20. Указания правила для определения принадлежности элементов множеству
Способы записи множеств.
10.
,
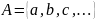где
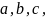… – элементы множества А.
20.
,
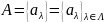где
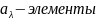множества
А,
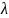– их индексы,
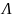– множество индексов.
30.
,
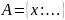где за знаком «:» следует правило для
определения принадлежности элементов
множеству А.
Операции над множествами.
10.
Объединением (суммой) множеств А и В
называется множество
,
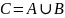которое состоит из элементов, принадлежащих
хотя бы одному из множеств А,В: (при этом
допускается, элемент принадлежит как
множеству А, так и множеству В):
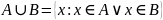
20.
Пересечение (произведением ) множеств
А и В называется множество
,
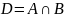которое состоит из элементов, принадлежащих
сразу обоим множествам А и В (то есть
элементов, общих для этих множеств):
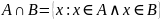
Определение:
Разностью множеств А и В называется
такое множество
,
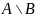которое состоит из тех же элементов
множества, которые не принадлежа
множеству В:
.
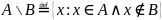Определение: Пусть (В – подмножество множества А). Тогда множество называется дополнением множества В до множества А:
.
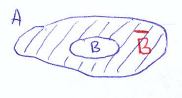
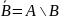Простейшие свойства операций над множествами.
1.0
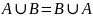
2.0
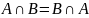
10 и 20 свойство называется коммутативностью соответствующей операции
3.0
(
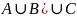= А
(В
С)
4.0
(А
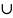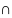В)
С = А
(В
С)
30 и 40 свойство ассоциативности соответствующей операции
5.0
(А
В)
С = (А
С)
(В
С)
свойство дистрибутивности