29) Максимально полезная внешняя работа.

Максимальная полезная внешняя работа   представляет собой работу, которую производит система над внешним теплоизолированным от системы объектом работы в обратимом процессе 1-2 работу, которую должен затратить внешний источник работы, чтобы вернуть систему из состояния 2 в исходное состояние 1 в тех же самых условиях, т.е. работу обратного обратимого процесса 2 - 1 называют минимальной работой; при этом  .

В самом общем случае  состоит из двух частей: работы, связанной с изменением объёма, и работы  , не связанной с изменением объёма.

В дальнейшем рассматриваются следующие два случая: 1) работа производится одиночным однородным телом при наличии источников тепла разной температуры; 2) работа производится телом. Находящимся в окружающей среде, давление  и температура   которой неизменны.

30) Энтальпия — это свойство вещества, указывающее количество энергии, которую можно преобразовать в теплоту.

Энтальпия — это термодинамическое свойство вещества, которое указывает уровень энергии, сохраненной в его молекулярной структуре. Это значит, что, хотя вещество может обладать энергией на основании температуры и давления, не всю ее можно преобразовать в теплоту. Часть внутренней энергиивсегда остается в веществе и поддерживает его молекулярную структуру. Часть кинетической энергии вещества недоступна, когда его температура приближается к температуре окружающей среды. Следовательно, энтальпия — это количество энергии, которая доступна для преобразования в теплоту при определенной температуре и давлении. Единицы энтальпии — британская тепловая единица или джоуль для энергии и Btu/lbm или Дж/кг для удельной энергии.

31) Свободная энергия Гельмгольца

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

, где U — внутренняя энергия, T — абсолютная температура, S —энтропия.

Отсюда дифференциал свободной энергии равен:

.

Видно, что это выражение является полным дифференциалом относительно независимых переменных T и V. Поэтому часто свободную энергию Гельмгольца для равновесного состояния выражают как функцию  .

Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

,

32) Свободная энергия Гиббса.

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, илитермодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на принципиальную возможность протекания химической реакции; это термодинамический потенциал следующего вида:

Энергию Гиббса можно понимать как полную  химическую энергию системы (кристалла, жидкостии т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж)

33) Химический потенциал.

Используя свойства экстенсивности термодинамических потенциалов, математическим следствием которых является соотношение Гиббса-Дюгема, можно показать, что химический потенциал для системы с одним типом частиц есть отношение энергии Гиббса к числу частиц в системе:

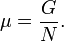
Если система состоит из частиц нескольких сортов i с числом N_i частиц каждого сорта, то соотношения Гиббса-Дюгема приводят к выражению

Химический потенциал применяется при анализе систем с переменным числом частиц, а также при изучении фазовых переходов. Так, исходя из соотношений Гиббса-Дюгема и из условий равенства химических потенциалов μ₁ = μ₂ находящихся в равновесии друг с другом фаз, можно получить уравнение Клапейрона-Клаузиуса, определяющее линию сосуществования двух фаз в координатах(p,T) через термодинамические параметры (удельные объёмы) фаз и теплоту перехода между фазами.