83. Матричный метод

Если радиационная задача содержит более четырех или пяти отдельных поверхностей, усилия и время, необходимые для определения плотностей тепловых потоков и температур поверхностей методами, становятся слишком большими, так что оправдано получение решения с помощью вычислительной машины. С увеличением числа поверхностей необходимо привести определяющие уравнения в систематический вид и применять стандартные математические методы для их решения. Одним из простейших, но и наиболее мощных методов, который можно использовать для анализа задач по излучению такого типа, является матричный метод. Если уравнения для плотности теплового потока можно привести к матричному виду, то для определения неизвестных параметров можно применить стандартные матричные методы, такие, как обращение матрицы. Когда число поверхностей, входящих в задачу, становится большим, обращение матрицы может быть запрограммировано для ЭВМ и решения, которые обычно требуют большого количества времени при ручном счете, можно получить очень быстро.

Матричные уравнения, используемые в случае, когда на поверхностях заданы температуры, несколько отличаются от матричных уравнений, используемых, когда на поверхностях заданы плотности тепловых потоков.

Этот метод используют, если необходимо определить несколько цветов. Метод основан на матричном уравнении: CIE X, Y, Z

представляет собой координаты цвета, RGBпредставляет собой цифровые значения датчика цвета. Матричные коэффициенты C00,

C01, C02, C10, C11, C12, C20, C21 и C22 определяются на основе выходных сигналов эталонного датчика цвета. Как только эти мат-

ричные коэффициенты определены, значения X, Y, Z могут быть рассчитаны из RGB значений датчика цвета.

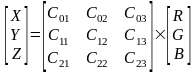
84.Перенос излучения в поглощающих пропускающих средах

ПЕРЕНОС ИЗЛУЧЕНИЯ, распространение эл.-магн. излучения (напр., оптического излучения) в среде при наличии процессов испускания, поглощения или рассеяния. Процесс П. и. представляет собой пространственно-частотное преобразование поля излучения, характеризующегося распределением интенсивности излучения по частотам, координатам и направлениям переноса лучистой энергии. Поле излучения полностью определяется заданием спектр. интенсивностей излучения Iv=Iv(r, W, t), таких, что величина IvdvdWdSdt есть кол-во лучистой энергии в спектр. интервале (v, v+dv) и в телесном угле dW, протекающей за время dt через площадку dS, помещённую в точке r перпендикулярно выбранному направлению.

Прохождение пучка света через в-во сопровождается его ослаблением вследствие поглощения и рассеяния квантов света или усилением вследствие процессов вынужденного и спонтанного испускания и рассеяния. Изменение спектр. интенсивности излучения подчиняется осн. ур-нию П. и., получаемому из условия баланса излучения в среде и представляющему

собой дифф. ур-ние в частных производных относительно интенсивности, как функции координат, времени и направления. В общем случае ур-ние П. и. не решается, однако в конкретных задачах допускаются упрощения и решение возможно. Так, для стационарного поля излучения изменение интенсивности при прохождении параллельного пучка в среде с малой частотной дисперсией есть dI/dx=-cI, где c характеризует суммарное ослабление света в среде с учётом процессов поглощения, вынужденного испускания и рассеяния. Решение этого ур-ния приводит к известному экспоненциальному закону ослабления света с расстоянием х (Бугера — Ламберта — Бера закон).