71.Аналогия Рейнольдса при турбулентном обтекании плоской пластины

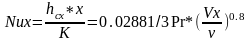
Можно видеть, что при конвективном теплообмене в турбулентном пограничном слое локальный коэффициент теплоотдачи уменьшается с увеличением расстояния х следующим образо. Из уравнения следует, что по сравнению с ламинарным течением, при котором коэффициент теплоотдачи при турбулентном течении уменьшается с увеличением х менее интенсивно и что при данном числе Рейнольдса этот коэффициент оказывается намного больше своего значения для ламинарного течения.

72 Вынужденная конвекция при ламинарном течений в трубе

Коэффициент теплоотдачи при ламинарном течении в трубе будем определять для полностью развитого течения и постоянного теплового потока на стенке. Для вывода уравнения сохранения энергии в данном случае рассмотрим небольшой цилиндрический элементарный объем, имеющий длину dx, внутренний радиус г и наружный радиус r+dr . Тепло входит в объем и выходит из него в радиальном направлении в результате теплопроводности, в то время как конвективный перенос энергии происходит в осевом направлении. Тепловой поток, входящий в элементарный объем вследствие теплопроводности.

Результирующий тепловой поток, выходящий из элементарного объема вследствие теплопроводности.Скорость движения через элементарный объем в осевом направлении постоянна, но при этом в нем происходит изменение температуры. В результате конвективного переноса в элементарный объем входит тепловой поток

Приравнивая результирующие тепловые потоки, обусловленные теплопроводностью и конвекцией при установившихся условиях. получаем уравнение энергии для ламинарного течения в трубе

С практической точки зрения обычно удобнее относить число Нуссельта к разности между среднемассовой температурой жидкости и температурой на поверхности стенки. Среднемассовую температуру жидкости обычно называют температурой смешения и получают путем сбора жидкости, истекающей из канала в специальный сосуд, и ее полного перемешивания. Естественно, что на входе в трубу температура постоянная, и поэтому среднемассовая температура и температура на оси трубы идентичны. Если число Нуссельта и коэффициент теплоотдачи определяются по разности температур между среднемассовой температурой жидкости и температурой поверхности стенки, то можно получить следующее значение этого Nu₀ = 4,36. Следует отметить, что значение числа Нуссельта при полностью развитом ламинарном течении не зависит от числа Рейнольдса, так как в этом случае толщина пограничного слоя просто равна радиусу трубы. Однако на начальном участке трубы значение числа Нуссельта будет больше, чем при полностью развитом течении.

73 Безразмерные комплексы, используемые для обобщения экспери­ментальных данных по конвективному теплообмену

В общем случае выбор физических параметров, необходимых для решения данной задачи по конвективному теплообмену, тре­бует определенного предварительного рассмотрения физического смысла процесса. Но после того, как такие параметры установ­лены, теория размерностей позволяет связать их в несколько безразмерных комплексов, точная функциональная зависимость между которыми может быть определена из эксперимента. Что­бы проиллюстрировать такой подход, найдем безразмерные комплексы, определяющие число Нуссельта при вынужденном течении в длинной гладкой трубе.

Зависимой переменной в рассматриваемом случае является коэффициент конвективной теплоотдачи . Для несжимаемого низкоскоростного течения независимыми переменными, опреде­ляющими коэффициент теплоотдачи, являются скорость жидко­сти V, линейный размер (т. е. диаметр трубы D) и такие физи­ческие свойства жидкости, как коэффициент теплопроводности k, коэффициент динамической вязкости µ, удельная теплоем­кость с_р и плотность р.

Независимые размерные величины, используемые в теории размерностей — масса М, длина L, время 0 и температура Т.