25. Алгебраические критерии устойчивости систем управления: критерий Гурвица.
Определитель Гурвица имеет размерность nxn, где n – порядок хар-ого ур-ия
Определитель составляется так:
1) по главной диагонали сверху вниз записывают коэф-ты а, начиная с an-1
2) Все столбцы формируют так: вниз от диагонали записывают коэф-ты по возрастанию, а вверх – по убыванию. Недостающие поля заполняются нулями.
Далее формируются все главные диагональные миноры:
Формулировка критерия:
Д
ля
того, что бы линейная САУ была устойчивой
необходимо и достаточно что бы при
an>0,
определитель Гурвица, построенный по
характеристическому ур-ию САУ, а также
все его главные диагональные миноры
были положительными. Если хотя бы 1 из
них <0, то САУ неустойчива, если хотя
бы 1 из них =0, то САУ нах на границе
устойчивости. Если an<0,
то полином нужно умножить на -1.
Достоинством этого метода явл. отсутствие вычисления корней и легкость алгоритмизации, позв. опред. уст-сть замкн. и разомкн. систем. Удобен при ручном счёте.
Н
едостаток:
исследовав устойчивость разомкнутой
САУ ничего нельзя сказать о замкнутой
САУ; если система неустойчива то ничего
неизвестно о том какой коэф-т надо
поменять, что бы она стала устойчивой.
Имеет ограничение на порядок, не больше
5. Рассм частные случаи: 1) для уст-сти
системы 1-го порядка необх. и дост-но,
чтобы коэф-ты хар-го полинома были >0
(C0p+C1;
Г=(С1)>0; 2) для уст-сти сист. 2-го
порядка необход. и дост., чтобы коэф-ты
хар-го полинома были>0
3) для уст-сти сист. 3-го порядка необход. и дост., чтобы при всех
положит-х коэф-ах хар-го полинома 2-й определитель Гурвица был
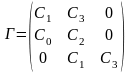
положительным.
4) для уст-сти сист. 4-го порядка необход. и дост., чтобы при всех положительных коэф-ах хар-го полинома
3-й
опред-ель был положительным.
Если среди опред-ей Гурвица есть =0, то на границе устойчивости.
2 6. Алгебраические критерии устойчивости систем управления : критерий Рауса.
Может использоваться для разомкнутых и замкнутых систем любого порядка с использованием таблицы Рауса. Удобен для реализации на ЭВМ. Позволяет определить количество нулевых и чисто мнимых корней, а также количество правых корней.
Таблица Рауса:
1-ая строка: четные коэффициенты (0,2,4...)
2-ая строка: нечетные коэффициенты (1,3,5...)
Для устойчивости системы необходимо и достаточно чтобы все
коэффициенты 1-ого столбца таблицы имели один знак.
Область применения: А) анализ устойчивости как замкнутых, так и разомкнутых систем. Б) не имеет ограничения на порядок ДУ.
В) процесс вычисления легко автоматизировать. Г) позволяет опред.
кол-во правых корней. Для определения количества правых корней,
мнимых, нулевых.а)Кол-во правых корней опред-ся по кол-ву коэф-ов в 1-м
столбце со знак. («-»).b)Кол-во пар мнимых корней опред-ся по кол-ву нулей в 1-м
столбце в середине таблицы.с)Кол-во нулевых корней опред-ся по кол-ву нулей в
конце 1-го столбца.То есть, можно получить полную картину корней хар-го Ур-ия.