16. Типовые динам. Звенья. Идеально Запаздывающее Звено.

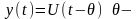постоянная времени чистого запаздывания [с]. Линии

электропередач, трубопроводы. Оказывает негативное влияние на работу системы. На основе

теоремы запаздывания получаем следующее выражение:

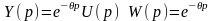
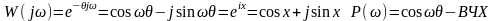
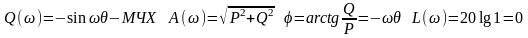АФЧХ.

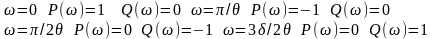АФЧХ данного звена представляет собой окружность единичного радиуса с центром в начале координат годографа АФЧХ начинается в точке (1; j0). Сама точка годографа движется по этой окружности по часовой стрелке. С периодом оборота 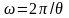ЛАЧХ.

17. Минимально фазовые и не минимально фазовые звенья. Минимально фаз.звенья описываемые обычно лин.диф.урав. полюсы и нули ПФ которых имеет отриц.или равные 0 вещественные части.

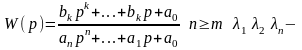корни нули. Особенность минимальных фазовых звеньев является, то что они имеют минимальное по модулю фазовый сдвиг ФЧХ по сравнению с любыми звеньями, имеющими такую же АЧХ, но у которых указаны условия о нулях и полюсах не соблюдаются все типовые звенья кроме звена чистого запаздывания являются минимальными фазовыми звенья. Не минимально фазовые звенья: 1) устойчивые.2) неустойчивые. 1) – это звенья описываются обычно линейными диф.урав., полюсы передаточной функции которого имеют отрицательные или равные 0 вещественные числа, а по ПФ имеют хотя бы одну вещественную часть. Не устойчивые не минимальные фазовые звено, это звено описываемое обычным лин.диф.урав. полюсы перед.функции которого имеют хотя бы одну полож.вещественную часть.

ПРИМЕР:

=

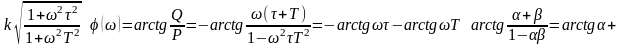
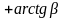
Соотв. рассмотренному звену, минимальное фазовое звено описывается уравнением

1-ого порядка следующего вида:

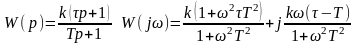
Из уравнения видно ω[0; + ) что применении меняется от 0 до некоторого max по модулю значения <чем π/2, затем возрастает к 0. Таким образом из полученный ур-ий видно, что АЧЗ рассмотренных звеньев совпадает, а ФЧХ не совпадает по модулю значительно меньше чем у не min-ого фазового звена.

ПРИМЕР. Звено чистого запаздывании. Если соответв.min-ое фазовое звено без инерционное 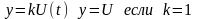т.к. у них будут одинак. АЧХ. Примером простейшего неустойчивого min-ого фазового звена является звено, описываемое диф-ым уравнением 1-ого порядка следующего вида:

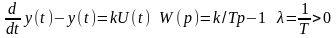
18.Основные определения и понятия о графах.

Для наглядного графического предсталения структур различных объектов и систем удобно применять граф:

Граф-это совокупность узлов(вершин) связанных между собой ветвями. Орграф(направленный граф)-это граф на ветвях которого указывается направление. Маршрут графа- это последовательность не повторяющихся ветвей графа в которой соседние ветви имеют один общий узел. Длина маршрута- кол-во ветвей участвующих в образовании маршрута. Контур графа- это маршрут графа который начинается и заканчивается в одном и том же узле.

Суграф графа – это подграф графа содержащий все еще узлы, но не задержаний всех его ветвей.

Дерево связанного графа (или дерево графа) – это связанный подграф графа без контуров.

Фундаментальное дерево графа – это связанный суграф графа без контуров. у деревьев графа выделяет понятия ветвей дерево и хорды дерево. Ветви дерево графа – это ветви графа, кот. входит данное дерево.

Хорды дерево графа – это ветви графа, не вошедшие в данное дерево. Взвешенный граф – это граф кот. узлам ставятся в соответствия некоторые сущности (объекты, сигналы и прочие), а ветвям ставятся в соответствие некоторые величины или зависимости определяющие взаимосвязь между соответствующими сущностями либо наоборот: ветвям – сущность, а узлам – зависимости. В технике чаще всего применяются след. разновидности графов: 1. структурная схема – это разновидность взвешенного графа, в кот. узлы обозначают элементы система управления, а направленные ветви обозначают сигналы между этими элементами, а также выходные и входные сигналы САУ. 2. Сигнальные графы. В них узлы обозначают входные, выходные и внутренние сигналы САУ, а ветви (стрелки) обозначают взаимосвязь между этими сигналами. 3. Эквивалент схема. В основном применяются в электронике и электротехнике и представляют собой разновидность взвешенного графа, в кот. ветви представляют собой элементы схем (сопротивления, индуктивности, источника ЭДС), а узлы определяют связи между этими элементами.

19.Общие сведения о структурных схемах: структурная схема, элемент, сигналы, точки съема, сумматоры. Порядок составления структурных схем. Для наглядного изображения САР и САУ используется:1)графы.2)структурные схемы. Структурная схема-это условное графическое обозначение САР и САУ, показывающее элементы системы и связи между ними. Основные компоненты:1)элемент(прямоугольник, в который вписывается ПФ).2)сигналы(входные или выходные) в виде стрелок: одинарная- для скалярных величин, двойная для векторных + их значение величин.3)точка разветвления(съёма)-место дублирования сигнала на схеме.4)сумматор- осущ-ий сложение нек-ой совокупности сигналов, вход всегда один, выходов м.б. много.(вычитателем может быть). В ТАУ системы скалярные, т.е. 1 вход и 1 выход, тогда для них действует порядок составления схем: 1)систему разбив-т на Эл-ты с 1-м вх.-м и 1 вых-дом 2) для каждого Эл-та пишут ДУ 3) для каждого Эл-та пишут П.Ф. 4) на листе изображ-ют Эл-ты схемы, соот-ие Эл-ам системы. 5) там же изобр-ют сигналы, связ-ие вх. и вых. переменные Эл-ов системы (по мере потребности включают сумматоры и точки съёма).В результате получают схему, в которой нет сигналов, идущих неизвестно откуда, и идущих неизвестно куда, кроме входа и выхода.

Для наглядного изображения САР и САУ исп-ся: 1)графы 2)структ. схемы. С.С.-это усл-ое графическое обозначение САР и САУ, показывающие элементы системы и связи м\у ними. Осн. компоненты:1) элемент (прямоугольник, в кот. впис-ся П.Ф.).2) сигналы (вход. или выходн.)в виде стрелок: одинарная-для скаляр. велечин, двойная- для векторных| +их значение величин. 3)точка разветвления (съёма)-место дублирования сигнала на схеме

4) сумматор- осущ-ий сложение нек-ой совокупности сигналов, вход всегда один, выходов м.б. много.(вычитателем может быть) В ТАУ системы скалярные, т.е. 1 вход и 1 выход, тогда для них действует порядок составления схем:

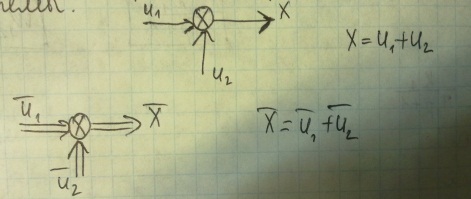1)систему разбив-т на Эл-ты с 1-м вх.-м и 1 вых-дом 2) для каждого Эл-та пишут ДУ 3) для каждого Эл-та пишут П.Ф. 4) на листе изображ-ют Эл-ты схемы, соот-ие Эл-ам системы 5) там же изобр-ют сигналы, связ-ие вх. и вых. переменные Эл-ов системы (по мере потребности включают сумматоры и точки съёма) В рез-те получают схему, в кот-ой нет сигналов, идущих неизв. откуда, и идущих неизв. куда, кроме входа и выхода.