1.ЭНЕРГЕТИЧЕСКИЕ ДОМЕНЫ И ПРЕДМЕТ ИЗУЧЕНИЯ ТАУ. Существ. техн.системы разнообразны, однако фундаментальные науки выявили простые параллели, отражающие сходство техн.систем. разной физической природы. В технике или в физике можно выделить ряд областей: системы относящиеся к одной области описываются при помощи правил в которых применены для описания, относящиеся ко всем остальным областям. Эти области называются энергетические домены. Домены бывают:

1) энергетические 2) магнитные 3) термальные

4) гидравлические 5) механические 6) акустические

7) ротационные. Для всех доменов справедливы 2 фундаментальных постулата: 1) Материя не может появиться ниоткуда и не может никуда исчезнуть.

2 ) Энергетический потенциал не может появится ниоткуда и не может никуда исчезнуть. Эти постулаты имеют свои формулировки для каждого домена. В электрическом домене – 1-й 2-й законы Кирхгофа. В каждом домене можно выделить переменные 2-х типов: 1) «поток» 2) «потенциал». Если рассматривать конкретную систему, то набор таких переменных описывается системами называемыми фазовыми переменные системы и фазовые координаты. Парные переменные системы могут связываться при помощи одного из 3-х законов: 1) аналог закона Ома U = IR Два других закона отражают св-ва элементов накапливать энергию. В каждом домене произведение 2-х парных элементов даёт мощность. Математическое описание системы из разных доменов является подобным. Исследования этого описания является предметом изучения теории автоматизированного управления. В последние годы приобретён успешный опыт методов СУ в экономике, в финансовых, в социальных и других, не технич. системах. ОСНОВЫЕ ОПРЕДЕЛЕНИЯ, ПРОБЛЕМЫ, ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. Управление в технике – это процесс оказания целенаправленных внешних воздействий на некоторый объект, для достижения заданной цели. Цель управления – некоторый показатель, либо совокупность показателей кол-но характеризующая качество процесса управления. Объект управления – это нечто (устройство, машина или комплекс машин), на что оказывается целенаправленное воздействие для достижения цели управления. Система управления – это совокупность управляемого объекта (или нескольких объектов) и средств управления этим объектом или объектами. Регулирование – частный случай управления, когда целенаправленно воздействию координат объекта. Система регулирования – это совокупность объекта регулирования и средств регулирования этой фазовой координатой. САУ – это система управления в которой сам процесс управления осуществляется автоматически, без участия человека. САР (система автомат. рег.) – это система регулирования в которой сам процесс регулирования осуществляется автоматически. В модели любого объекта или системы выделяют величины двух видов. Параметрами будем называть такие величины моделей, максимально возможная скорость изменения которых незначительна в отличии от скорости изменения переменных модели. Большинство случаев параметры модули можно принимать постоянные величины. На работу системы управления влияют различные факторы, как переменные, и их мы будем называть внешние воздействия. Внешние воздействия бывают 3-х видов: 1) возмущающие возд. – это воздействия оказываемые на различные элементы системы управления и мешающие её нормальной работе. 2) задающие возд. – это воздействия которые определ. заданные, то есть желаемые значения управляемых переменных системы. Управляемые переменные это те которые представляют y(t) выходные переменные системы. 3) Управляющие или регулирующие возд. – это воздействия осуществ. целенаправленное управление системой. Формируются средствами управления (регулятор) и непосредственно воздействуют на объект управления. Их цель ликвидировать влияние возмущений и обеспечить изменение выходных переменных системы согласно задающим воздействия. Переменная характер. состояние объекта управления называется его выходными величинами (управляемая переменная). Места их проявления называют выходами объекта. Управляющие и возмущающие воздействия, оказывающие, влияние не объект называются его входными величинами, а места их воздействия называются входами объекта.

2. КЛАССИФИКАЦИЯ САР И САУ. Признаки, не оказывающие влияния на поведение системы с точки зрения ТАУ: 1) Физическая природа сигналов протекающих в синтезе и отличия её работы.

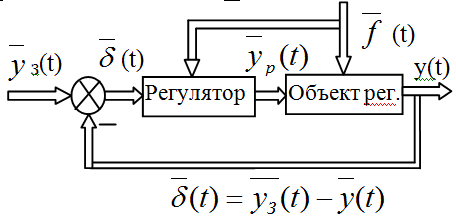
2) Конструктивное исполнение элементов системы: датчики, резисторы, исполнительные механизмы. Признаки оказывающие влияние на поведение системы: КЛАС-ИЯ ПО ВИДУ ЗАДАЮЩЕГО ВОЗДЕЙСТВИЯ. 1) Система стабилизации – это САУ в которых задающее воздействие постоянно или медленно изменяется с течением времени. 2) Системы программного управления – это САУ в которых задающее воздействие изменяется по заранее заданному з-ну в виде функции от времени (приводы станков с ЧПУ). 3) Следящая система – это САУ в которых задающее воздействие изменяется произвольным образом по неизвестному заранее з-ну. Однако обычно известны предельные характеристики этого з-на (мак.скорость, ускорение).КЛАС-ИЯ ПО НАЛИЧИЮ ОБРАТ. СВЯЗЕЙ И З-НОВ УПРАВ. 1) Разомкнутые системы – системы без обратных связей: а) системы без регулирования по возмущению. В таких системах аппарат теории управления используется в меньшей степени. f(t) – возмущение, негативно влияет на систему. Поэтому такие САР используются только в случаях когда возмущающим воздействием можно пренебречь (станки ЧПУ с часовым двигателем). б) Системы с регулированием по возмущению. Они могут быть реализованы если возмущающие воздействия могут быть изменены или вычислены каким-либо образом. 2) Замкнутые системы – это САУ у которых есть обратная связь: а) Системы с контурным управлением – это системы в которых чётко определяются одни или несколько обратных связей по скалярно-регулируемым величинам (*). Регулятор имеет один из 5 видов:

1) П-регулятор – реализуетпропорционал. закон регулированияy_р(t) = kδ(t) где k – коэф. пропорцион.

2) И-регулятор – реализующий интегральный закон управления

постоянная величина времени интегрирования регулятора.

3) ПИ-регулятор – реализующий

пропорционально интегральный з-н управления

4) ПД-регулятор – реализ. пропорц. диф. з-н управления:

постоянная времени диф-ия регул. Физически нереализуема. Реализуется приближенно. 5) ПИД-регулятор – реализ.пропорц.интегр. з-н диф.управления:

б) Системы с многосвязным управлением – это замкнутое САУ в которых выдел. один контур обратных связей по вектору регулируемых величин. Здесь в состав системы включают много связей регулятор, он преобраз. вектор ошибок системы в вектор управляющих воздействий.

3. КЛАС-ИЯ САР И САУ. Признаки, не оказывающие влияния на поведение системы с точки зрения ТАУ: 1) Физическая природа сигналов протекающих в синтезе и отличия её работы. 2) Конструктивное исполнение элементов системы: датчики, резисторы, исполнительные механизмы. Признаки оказывающие влияние на поведение системы: КЛАС-ИЯ ПО МАТЕМАТ. ПРИЗНАКАМ. 1) В зависимости от лин.ур., записывающих систему: а) Линейные системы – это САУ, поведение которых описывается совокупностью лин. алгебраических и диф-ых уравнений. Для таких систем справедлив принцип суперпозиции: при воздействии на вход САУ суммы некоторых сигналов, выходной сигнал будет являться суммой реакции САУ на каждый из этих реакции, если бы они подавались ни вход по отдельности. Делятся на стационарные и не стационарные. Стационарные – это САУ, поведение которых описывается ДУ с постоянным коэф. Нестационарные – это САУ, поведение которых описывается ДУ к которых коэф. являются функциями от времени. б) нелинейные системы-САУ, поведение которых описывается совокупностью лин. алгебраических и диф-ых уравнений, среди кот-х есть хотя бы одно нелинейное Ур-ие. (такие системы не подч. принципу суперпозиции) Сущ-но-нелин-ые системы-нелинейные САУ, линеализация Ур-ий кот-х приводит к существ-й потере точности описания процессов, протек-х в системе. Системы с запаздыванием - разновидность нелинейных САУ, нелинейность в которых вызвана только лишь присутствием в них звеньев чистого запазд-ия. в) в зав-сти от дискретности Ур-ий: непрерывные-САУ, повед-ие кот-х опис-ся алгебр. и диф. Ур-иями, переменные в кот-х явл-ся непрерывными ф-иями от времени. Дискретные - САУ, повед-ие кот-х опис-ся алгебр. и диф. Ур-иями, переменные в кот-х явл-ся прерывистыми ф-иями от времени. Цифровые - это дискрет. САУ, управление в кот-х осущ-ся с помощью цифровых устройств или ЭВМ. г) в завис-ти от кол-ва независ-х переменных в ДУ системы: 1.Системы с сосредоточенными параметрами-САУ, описываемые совокупностью обыкновенных ДУ.2.Системы с распределёнными параметрами-описываются ДУ в частных производных. д) в зав-сти от наличия случ-х факторов в системе:

1.Детерминированные-САУ, описываемые Ур-иями, в кот-х отсутствуют случ. факторы. 2. Стохастические-САУ, описываемые уравнениями, в кот-х присутствует случ. фактор. КЛАС-ИЯ ПО ТИПУ ОШИБКИ в установившемся режиме:-статические(имеют установившуюся ошибку регул-ия; астатические-САУ, в кот-х отсутствует установившаяся ошибка регул-ия. ПО СП-БУ НАСТРОЙКИ САР или САУ: адаптивные-САУ, способные функц-вать при отсутствии полной информации об объекте упр-ия. Неадаптивные-САУ, в кот-х предполагается наличие полной информации об объекте упр-ия. Системы с самонастройкой параметров-САУ, опис-ся моделями с пост. структурой, где параметры меняются с течением времени. Системы с самонастройкой структуры-САУ, модели кот-х могут менять не только параметры с течением времени, но и свой вид.

4.Стандартные формы представления моделей САР и САУ. Пусть поставлена задача составления исходных ДУ САУ, тогда возможны 2 ситуации: 1)имеется возм-сть детальной декомпозиции системы на модули и отд. звенья, модели кот-х хорошо изучены(здесь применяют з-н сохр-ия энергии и материи и получают точную модель системы, она описывает процессы, протекающие в системе 2)из-за отсутствия дост-ой информ-ии о САУ или из-за малой изученности отдельных узлов, детальная декомпозиция невозможна(здесь ставят эксперимент, в рез-те кот-го получают грубую модель системы, её исп. для дальнейших исследований, для синтеза адаптивных систем. ||Для формализации процесса составления исходных ДУ систем, при получении истинной модели, исп-ют метод контур. токов и узловых потенциалов

(в каждом домене есть свои аналоги) Для удобства формализации решений модели САУ могут представляться в различных стандартных формах: Нормальная Коши, Пространства состояний, Передаточных ф-ий(САР) или перед-х матриц(САУ). НОРМ. ФОРМА КОШИ: в такой форме м.б. представлена любая нелинейная САР или САУ с гладкими нелинейностями. Это наиболее общая форма записи системы ДУ, разрешённых исключ-но отн-но первой производной координат САР или САУ. Эта форма удобна для численного решения системы ДУ на ЭВМ. Для нелинейности систем при нулевых нач. условиях форма м.б. представлена в след-м виде:

-вектор внутр. координат(переменных состояния.

Пусть САР или САУ явл-ся линейной, т.е. опис-ся линейным ДУ с пост. коэф-ми. Тогда модель примет след-ий вид:

САР и САУ)

-вектор задающих и возмущающих воздействий

САР или САУ (вектор вход.воздействий)

5.ФОРМА ПРОСТР-ВА СОСТОЯНИЙ. Это матричная форма записи системы ДУ объектов управления, САР или САУ, адаптированная для управления путём выделения из норм-ой формы Коши системы алгебр-х Ур-ий, кот-ые связ-ют внутр-ие корд-ты объекта или системы с выходными переменными. Форма удобна для описания систем высокого порядка с нескл. входами и выходами. В любой САУ можно выделить строго фиксир-ое кол-во переменных, кот-ое в совокупности опис-ет её динамику. Это кол-во наз-ся порядок системы. Эти переменные зависят от времени и могут меняться при изменении внешних воздействий. Вместе они хар-ют сост-ие системы в некот. момент времени,поэтому они наз-ся переменные состояния системы. Обл-сть или пространство всех возможных значений этих переменных наз-ся пространством состояния объекта или системы. Траектория изменения с течением времени радиус-вектора переменных состояния системы или объекта в пр-ве сост-ия наз-ся траектория движения системы или объекта. Любое положение

рад.-вектора предст. собой состояние пространства состояния.x(t)-вектор перем-ых состояния объекта, сист., U(t)-вектор входных воздействий САУ,

y(t)-вектор выходных переменных САУ (m-кол-во входов, q-кол-во выходов)

Тогда в самом общем виде модель непрерывной САУ в пр-ве сост-ий м.б. представлена системой из двух векторных уравнений:, где f,g-вектор-ф-ия, X0-нач. условия. 1-ое матричное Ур-ие сост-ия САУ-из него видно, что вектор состояния опред-ся в любой момент времени ч-з вектор вход. воздействий и ч-з нач.-ые значения переменных состояния.

2-ое матричное Ур-ие сост-ия САУ-из него следует, что вектор выход.-х воздействий переменных всегда однозначно выделяяется через…

1*

2*

Пусть нач-ые усл-ия нулевые, тогда систему * представим в след-ем виде:

Пусть система линейная, тогда представим модель в след. виде:

Система линейная и стационарная, тогда матрицы А, В, С, D,-матрицы численных коэф-ов: распишем их:

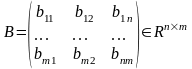
Матрица А-состояния, опис-ет динамику объекта, В-определяет структуру входного устройства системы (входная), С-определяет структуру выходного устройства системы (выходная), D-напрямую связывает выход. переменные с входными воздействиями (вход-ввходная). **

В развёрнутом виде ** выглядит след-им обр-ом:

Моделям соот-ет след-ая структурная схема:

Пусть m=1, q=1, тогда система скалярна, в противном случае –векторная, в этом случае модель (*) примет вид:

описание в этой форме строго формализовано, не требует понимания физ-ой природы процессов, текущих в объекте.

При этом структура модели имеет вид (слева), есть недостаток- потеря описания внутренней структуры системы.

Такая форма поддерживается всеми осн-ми системами комп-го моделирования. если форма применена обоснованно, то модель явл-ся истинной

6. Сущность и основные свойства преобразования Лапласа

Изображение Л - f(p)-функция интеграла p-комплексная переменная;

F(p)=Z{f(t)} Основные свойства

1 Линейность, т.е. линейность комплектации оригинала соотв. такая же лин. комбинация

изображения

2 n-кратному дифф. Оригинала соответствует (степень) умножения на p в степени n

3 интегралу соответ. деление на рлп.

4 Теорема запаздывания смещение аргумента оригинала на величину a соотв. умножения оригинала на величину

5 смещение аргумента изображения на величину a соотв. умножения функции на величину

6 Теорема масштабов умножение аргумента оригинала на постоянную величину a соотв. делению изображения и его аргумента на величину a

7 Теорема о нач и конеч значениях оригинала

8. Действие, обратное действию преобразования Лапласа-обратное преобразование Лапласа:

Процесс решения ДУ с использованием преобразований Лапласа:

1)ДУ или система ДУ запис-ся в операторной форме(переменные заменяются их изображениями) X(t)-X(p); U(t)-U(p).,а их производные и интегралы-

их изображениями, умноженными или разделёнными на оператор Лапласа Если нач. усл-ия ненулевые, то они учитываются ч-з

теорему о дифференцировании оригинала. В рез-те система ДУ превращ-ся в систему алгебр. Ур-ий. 2)В этой системе алг Ур-ий изображения искомых

переменных выражаются ч-з изображения известных переменных. 3) Задаваясь конкретными ф-иями от времени для известных переменных по

таблицам находят изображения этих ф-ий, и подставляют их в Ур-ия вместо изображения известных переменных. 4)по справочным таблицам выпол-

няют обратное преобразование Лапласа. В рез-те находят искомые переменные, но уже в виде ф-ий от времени.

Вывод применение изображения Л позволяет заменить операции диффер. и интегрирования на обычные алгебраические позиции

7. Передаточная функция динамической системы. Свойства передаточной функции.

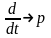
- полином выхода

- полином входа

Чем сложнее полином, тем сложнее система

W(p)-передаточная ф-ция

Передаточной функцией САУ является отношение изображения по Лапласу на входе системы к изображению по Лапласу сигнала на входе. Передаточная функция является основой, избыточной характеристикой линейной динамической системы.

Основные свойства передаточной функции:

1) ПФ является дробно - рациональной функцией от параметра p, который в данном представлении может рассматриваться как алгебраический.

2) Коэффициенты ai и bj – числа вещественные и постоянны для стационарной системы, они отражают действительные физические характеристики системы.

3) В реальных физических системах, как правило, n≥m, т.е. порядок знаменателя выше, чем порядок числителя. Это отношение выражает инерционность любых реальных объектов и соответствует принципу физической реализуемости. Никакие изменения на выходе не могут произойти раньше изменения на входе. Случай n<m возможен только для отдельных элементов системы.

4) ПФ имеет «нули». Это значения p, обращающие в нуль числитель, т.е. это корни уравнения Mm(p)=0 =>p1, p2,…, pm

ПФ имеет «полюсы». Это значения p, обращающие в нуль знаменатель, т.е. корни уравнения Dn(p)=0, p1, p2,…, pn

Нули и полюсы могут быть как веществ., так и комплексными. Полюсы важнее для задач анализа и синтеза в ТАУ по 2 причинам:

1) они могут означать резкое возрастание выходного параметра, а это есть неустойчивость САУ.

2) уравнение могут рассматриваться без правых частей. В свободном движении САУ (ДУ без правой части) нули не имеют никакого значения.

Сложность ПФ, а именно макс. степень полинома, определяет сложность (порядок) САУ.