Описание в виде алгебраического выражения
Пример: f(x1, x2, x3) = (x1+x2)∙x3 + (x1+x3)∙x2 + (x2+x3)∙x1 = x1∙x3 + x1∙x2 + x2∙x3
Описание в виде последовательности десятичных чисел
Каждому набору (x1, x2,…, xn) можно поставить в соответствие двоичное число, а каждому двоичному числу – его десятичный эквивалент. Тогда функцию можно задать в виде: f(Di,…Dj) = 0, f(Dk,…Dl) = 1. Для полностью определенных функций, как правило, указывают только один вариант для f(x1, x2,…, xn)=1 (или для f(x1, x2,…, xn)=0). Функция называется полностью определённой, если её значение для n переменных однозначно определено на всех 2n входных наборах.
Пример: f(3,5,6,7)=1 (f(0,1,2,4)=0)
Также пишут: f(x1, x2, x3) = ∑(3,5,6,7) или f(x1, x2, x3) = \/(3,5,6,7)
f(x1, x2, x3) = ∏(0,1,2,4) или f(x1, x2, x3) = /\(0,1,2,4)
Геометрическое представление (кубические комплексы)
Основой геометрического представления является представление каждого входного набора в виде n-мерного вектора. Вершины этих векторов могут быть представлены как вершины n-мерного куба. Наборы переменных, расположенные на разных концах одного ребра и отличающиеся значением только одной переменной называют соседними.
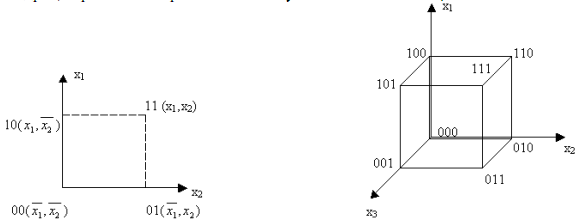
Отмечая точками вершины векторов, для которых значения функции равны 1, получают геометрическое представление функции в виде куба. Каждую такую вершину называют нулевым кубом (0-кубом). Совокупность 0-кубов называют нулевой кубический комплекс К0. Если 2 0-куба комплекса К0 отличаются только по одной координате (переменной), то они образуют единичный куб. Записывается 1-куб последовательностью общих элементов его 0-кубов с прочерками в несовпадающих местах. Он соответствует ребру n-мерного куба. Множество единичных кубов образуют единичный кубический комплекс К1. Если 2 1-куба комплекса К1 отличаются только по одной координате (переменной), то они составляют двоичный куб (2-куб). Он соответствует грани n-мерного куба. Множество 2-кубов составляют К2.
Размерность куба – его ранг – определяется числом несовпадающих координат, т.е. числом прочерков в его записи. Объединение кубических комплексов для функции n переменных образует ее кубический комплекс K(f)=\/(К0, К1, …, Кm).
Пример: f(x1, x2, x3) = ∑(3,5,6,7)
К0 = (011, 101, 110, 111) Т.к. 101 и 111 отличаются только 1 переменной, то они образуют 1-1 куб.
К1 = (1-1, 11-, -11) Т.к. нет 1-кубов, отличающихся 1 переменной, то нет и 2-куба.
Дайте определение термина «вентиль», «логическое устройство». Приведите УГО вентилей.
Элементы ЭВМ выполняют функции простейших преобразователей информации. Они реализуют различные логические операции над сигналами входных двоичных переменных, а также обеспечивают запоминание, формирование и преобразование этих сигналов.
По зависимости от выходного сигнала схемы можно условно разделить на:
Схемы первого рода - комбинационные, выходной сигнал в которых зависит только от состояния входов (наличия входных сигналов).
Схемы второго рода - накапливающие (элементы с памятью), выходной сигнал в которых зависит от состояния входов и предыдущего состояния.
Техническая реализация цифровых устройств требует использования соответствующих элементов. Комбинационные схемы выполняются на логических элементах; цифровые автоматы кроме логических элементов используют также запоминающие элементы, которые фиксируют их внутренние состояния.
Логический элемент (вентиль) – это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическое устройство – совокупность логических элементов, в котором выходы одних элементов являются входами для других.
Несмотря на огромно количество элементов, находящихся в составе ЭВМ, число их разновидностей (типов) относительно невелико.