2.2 Теорема отсчетов [д10]

Определение необходимого числа выборок можно объяснить очень просто. Предположим, что некоторым образом берутся выборки аналогового сигнала. Если по этим выборкам можно точно восстановить аналоговый сигнал, выборки были сделаны правильно.

На рис.2.3 показаны несколько синусоид a)…d) с разными частотами до и после дискретизации. Сплошная линия представляет сигнал на входе АЦП, квадратным маркером помечены отсчеты на его выходе. На a) аналоговый сигнал постоянен (с нулевой частотой). Поскольку аналоговый сигнал представляет собой прямые отрезки, соединяющие отсчеты, то вся информация, необходимая для его восстановления, содержится в цифровых данных, т.е. отсчеты сделаны правильно.

Рис.2.3

Синусоида, показанная на b), имеет частоту 0,09 от частоты выборки. Это можно представить, например, как синусоиду с частотой 90 Гц, выборки которой берутся с частотой 1000 Гц, т.е. на каждом периоде синусоиды делаются 11,1 выборки. Этот случай сложнее предыдущего, поскольку аналоговый сигнал не может быть реконструирован простым соединением отсчетов прямыми линиями. Правильно ли взяты выборки в этом случае? Ответ положителен, поскольку не существует другой синусоиды или комбинации синусоид (в рамках изложенных ниже ограничений), которые бы могли создать такое сочетание величин отсчетов. Только одна единственная синусоида с частотой 0,09 может быть их источником, поэтому и этот сигнал может быть восстановлен по отсчетам.

В случае c) частота синусоиды повышена до 0,31 от частоты выборки, т.е. на период синусоиды приходится только 3,2 отсчета. Здесь выборки настолько редки, что по ним трудно проследить тренд аналогового сигнала. Правильно ли взяты выборки в этом случае? Опять “да” и по тем же причинам – совокупность выборок является уникальным представлением аналогового сигнала. Вся информация, необходимая для реконструкции сигнала, содержится в цифровых данных. О том, как это сделать, будет сказано ниже.

В случае d) частота сигнала еще повышена до 0,95 от частоты выборки, т.е. на период приходится только 1,05 отсчета. Правильно ли взяты выборки в этом случае? Конечно же нет! Эта совокупность отсчетов может соответствовать различным синусоидам. В частности, по рисунку отсчетов видно, что они принадлежат синусоиде с частотой 0,05 от частоты выборки (хотя взяты из сигнала с частотой 0,95). Это явление изменения частоты синусоид при взятии отсчетов называется переносом спектра (aliasing). По совокупности отсчетов можно сделать ложный вывод о наличии в сигнале синусоиды, которой в действительности там нет. Поскольку цифровые данные больше не представляют уникально определенный сигнал, его реконструкция по ним невозможна. В цифровых данных нет информации, принадлежат ли отсчеты синусоиде с частотой 0,05 или с частотой 0,95 от частоты выборки, частота синусоиды скрыта. В соответствии со сделанным выше определением выборки сигнала взяты неправильно.

Эти рассуждения привели нас к одному из основных положений в цифровой обработке сигналов – к теореме отсчетов. Часто ее называют теоремой отсчетов Шеннона (Shannon) или теоремой отсчетов Найквиста (Nyquist) или теоремой Котельникова. Теорема отсчетов гласит, что непрерывный сигнал может быть адекватно представлен совокупностью отсчетов только в том случае, если не содержит компонент на частотах выше половины частоты выборки. Т.е. необходима частота выборки 2000 Гц для квантования сигнала, содержащего компоненты до 1000 Гц, если сигнал содержит компоненты с более высокими частотами, они будут перенесены в диапазон от 0 до 1000 Гц, сложатся с имеющимися там компонентами, исказят информацию и сделают восстановление сигнала невозможным.

При обсуждении теоремы отсчетов широко используется термин: частота Найквиста, однако он не имеет стандартного определения и может иметь различное значение. Наиболее часто под частотой Найквиста понимают половину частоты выборки.

На рис.2.4 показано, как частотные компоненты изменяются при переносе спектра. Ключевое положение, которое необходимо помнить – цифровой сигнал не может содержать частотных компонент выше половины частоты выборки (частоты Найквиста). Когда все частотные компоненты аналогового сигнала лежат ниже частоты Найквиста, они адекватно отображаются в цифровом сигнале. Однако, если в аналоговом сигнале присутствуют компоненты с более высокими частотами, они создают ложные образы (alias) в том частотном диапазоне, который может быть представлен совокупностью отсчетов. Как показано зигзагообразной линией на рис.2.4, компоненты с частотами выше частоты Найквиста создают ложные образы с частотами от нуля до половины частоты выборки. Если на этих частотах уже есть компоненты, ложные компоненты складываются с ними, т.е. информация теряется и о высших частотных компонентах и о низших.

Предположим, что в цифровом сигнале содержится компонента с частотой 0,2 от частоты выборки. Она должна формироваться от соответствующей компоненты аналогового сигнала с той же частотой, однако она может также возникнуть от бесконечного ряда компонент с частотами 0,8, 1,2, 1,8, 2,2 … от частоты выборки, причем фазы компонент с частотами в диапазонах от 0,5 до 1,0, от 1,5 до 2,0 и т.д. инвертированы.

На рис.2.5а показан пример аналогового сигнала. Его спектр изображен на рис.2.5b. Из рис. 2.5b видно, что сигнал содержит компоненты в диапазоне от 0 до 0,33f_s, где f_s – планируемая частота выборки. Это, например, может быть речевой сигнал, из которого предварительной фильтрацией удалены все компоненты с частотами выше 3,3 кГц, а f_s в таком случае 10 кГц.

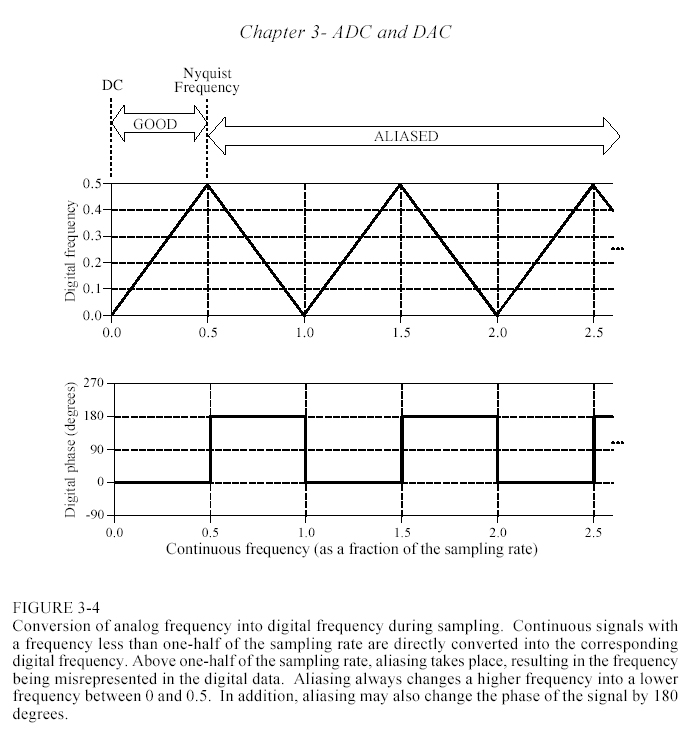
Рис.2.4

Этот сигнал квантуется последовательностью дельта-импульсов. Между импульсами величина сигнала равна нулю (рис.2.5с). Спектр квантованного сигнала приведен на рис.2.5d. Спектр содержит множество копий спектра исходного сигнала, воспроизведенных у частоты квантования f_s и ее гармоник 2f_s, 3f_s, 4f_s и .т.д., причем исходный спектр воспроизводится как справа от f_s, так и слева (зеркальная копия исходного спектра). Почему это происходит?

Спектр последовательности дельта-импульсов так же представляет собой последовательность дельта-импульсов, то есть последовательности бесконечно узких импульсов единичной высоты, генерируемых во временной области с частотой f_s, в частотной области соответствует ряд спектральных линий единичной высоты расположенных на частотах f_s, 2f_s, 3f_s, 4f_s и т.д. Взятие выборок можно представить как перемножение исходного сигнала с последовательностью дельта импульсов. При перемножении сигналов спектр произведения определяется сверткой исходных спектров.

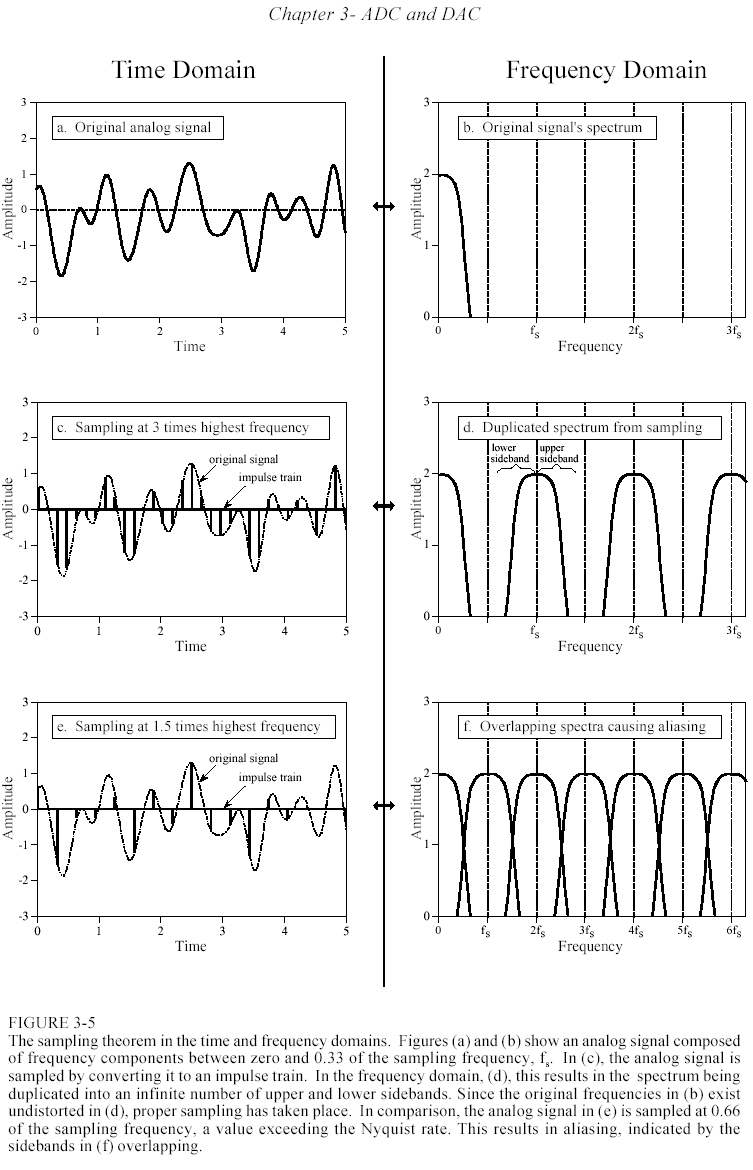
Рис.2.5

Итак, взятие отсчетов приводит к генерации новых частотных компонент и изменению спектра исходного сигнала. Возникает вопрос – правильно ли производится квантование? В случае рис.2.5с ответ положителен, поскольку сигнал можно восстановить, пропустив его через фильтр нижних частот и удалив все компоненты с частотами выше f_s/2. Т.е. аналоговый фильтр нижних частот может преобразовать цепочку импульсов рис.2.5с обратно в исходный аналоговый сигнал рис.2.5а.

На рис.2.5e показан пример неправильного квантования (слишком низкой частоты выборки). Аналоговый сигнал все так же содержит компоненты с частотами выше 3,3 кГц, но в этом случае f_s всего 5 кГц. Отметим, что частоты f_s, 2f_s, 3f_s, 4f_s и т.д. на рис.2.5f сдвинуты на горизонтальной оси ближе, чем на рис.2.5d. Из рис. 2.5f видна проблема: частотные спектры основной и репродуцированный перекрываются, а это значит, компоненты из их перекрывающихся частей складываются, формируя искаженную информацию. Поскольку нет средств для разделения перекрывающихся частотных компонент из этой смеси, информация о сигнале безвозвратно утеряна и сигнал невозможно восстановить. Такое перекрытие спектров имеет место, когда сигнал содержит в спектре компоненты с частотами, большими половины частоты квантования.