11. Преобразование характеристик случайного процесса в линейных цепях

Пусть на входе линейного четырехполюсника с импульсной характеристикой h(t) и частотной передаточной функцией H (j ) действует случайный процесс s_вх(t) с заданными характеристиками; требуется найти статистические характеристики выходного сигнала s_вых(t): распределение вероятностей, корреляционную функцию, спектральную плотность мощности.

Самой сложной из этих задач является первая. Она упрощается при нормальном распределении, так как при любых линейных операциях (усилении, фильтрации, дифференцировании, интегрировании) распределение остается нормальным, изменяются лишь функции R(t) и W( ), т.е. если задана плотность вероятности флуктуаций случайного процесса в виде

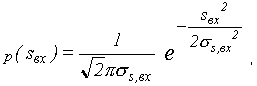
то плотность вероятности выходного сигнала

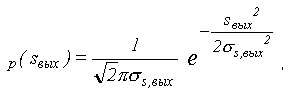
при этом дисперсия легко определяется по спектру или корреляционной функции.

16.Узкополосный случайный процесс

К узкополосным случайным процессам относят процессы, спектральная плотность мощности которых соредоточена в относительно узкой полосе частот в окрестности некоторой достаточно высокой частоты f₀ (рис. 2), то есть D f<<f₀.

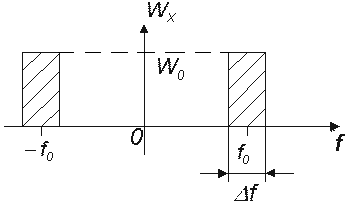  Рис. 2

Пример реализации такого случайного процесса показан на рис. 3, где C (t) - огибающая.

Рис. 3

Шумовое колебание с узкополосным спектром следует рассматривать как высокочастотное колебание с медленно изменяющимися огибающей X(t) и фазой q (t):

x(t) = X(t)cos[w ₀t+Q (t)] = X(t)cosY (t),

причем w ₀ является центральной частотой спектра шума. Мгновенные значения амплитуды X(t), фазы q (t) и частоты

вляются случайными функциями времени 

2 8.Отношение сигнал-шум на выходе оптимального фильтра

Т ак как пиковое значение выходного сигнала

где  -полная энергия сигнала, а мощность шума на выходе

то отношение пика мощности сигнала к мощности выходного шума равно  .

Таким образом, отношение сигнал-шум на выходе оптимального фильтра зависит от энергии сигнала на входе и не зависит от его формы, причем в этом случае обеспечивается максимально возможное отношение сигнал-шум, и следовательно, максимально возможная вероятность правильного обнаружения этого сигнала при заданном уровне вероятности ложной тревоги.

Е сли на входе приемника действует не белый шум, а шум, имеющий неравномерную спектральную плотность мощности, то оптимальный фильтр строится в виде последовательно соединенных двух линейных фильтров

П ервый фильтр выбирается таким образом, чтобы шум на его выходе стал белым, т.е. если на входе шум описывается характеристикой  , то на выходе фильтра должно выполняться   на всех частотах. Следовательно

Д ля сигнала   на выходе первого фильтра будем иметь

Х арактеристика второго фильтра должны быть согласована с сигналом  , т.е.

Частотная характеристика цепочки определяется выражением

Т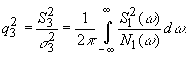 аким образом, такой оптимальный фильтр ослабляет те участки спектра входного колебания, которые соответствуют наиболее интенсивным спектральным составляющим шума.

Отношение сигнал-шум здесь составляет