6.Спектральная плотность мощности и корреляционная функция случайного процесса на выходе линейной цепи
Если входной сигнал обладает спектром мощности Wвх( ), то на выходе сигнал будет иметь спектральную плотность мощности
Wвых ( )=Wвх( ) H2( ).
Корреляционную функцию определим как обратное преобразование Фурье
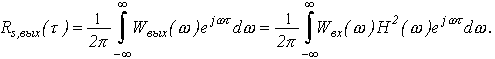
А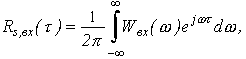
налогичные
записи можно провести на основе знания
импульсной характеристики цепи. Поскольку
спектральной функции Wвх() соответствует
корреляционная функция
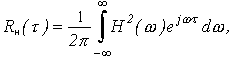
а спектральной функции H2( ) соответствует
то произведению Wвх() H2() соответствует свертка
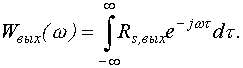
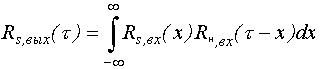
и
В случае белого шума на входе с Wвх( )=W0 имеем Wвых( )= W0H2, а
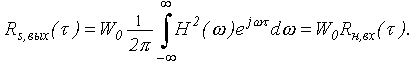
Это же выражение можно применить и для случая, когда спектральная плотность мощности случайного стационарного процесса на входе цепи равномерна лишь в полосе прозрачности цепи.
7. Теорема Винера –Хинчина
Энергетический
спектр и автокорреляционная функция
случайного процесса являются неслучайными
функциями, связанными между собой.
Установим эту связь. Рассмотрим
реализацию 
случайного
процесса длительностью 
и
ее копию 
,
сдвинутую на интервал времени 
.
Известно, что энергетический спектр и
автокорреляционная
функция детерминированного сигнала
связаны между собой парой преобразований
Фурье. Тогда с учетом выше приведенного
предположения о том, что реализация
и
ее копия
нам
известны, можно записать
.
Разделим обе части этого равенства на
,
(5.62)
и
устремим 
.
Тогда
в соответствии с (5.51) левая часть равенства
(5.62) представляет собой автокорреляционную
функцию 
.
Учитывая (5.59) равенство (5.62) можно
представить следующим образом
.
(5.63)
Но это есть обратное преобразование Фурье, связывающее АКФ случайного процесса с его энергетическим спектром. Очевидно, если существует обратное преобразование, значит, существует и прямое преобразование Фурье
,
(5.64)
связывающее энергетический спектр с АКФ.
Таким образом, АКФ случайного процесса и его энергетический спектр связаны между собой парой преобразований Фурье. Впервые эта связь была установлена советским математиком А. Хинчиным и независимо от него американским ученым Н. Винером. Поэтому соотношения (5.63) и (5.64) носят название теоремы Винера–Хинчина.
Так
как автокорреляционная функция
и
энергетический спектр 
являются
вещественными четными функциями, можно
отказаться от комплексной формы записи
преобразования Фурье и перейти к другой
форме
,
(5.65)
.
(5.66)
Из этих выражений следует
,
(5.67)
.
(5.68)
Но 
,
откуда
,
что совпадает с (5.60).
В случае, когда энергетический спектр описывается функцией циклической частоты (5.61), выражения (5.65) – (5.68) приобретают вид
,
(5.69)
.
(5.70)
,
(5.71)
.
(5.72)