6. Типы переменных в эконометрических моделях

эндогенные – образуются внутри модели. Экзогенные – не зависят от

модели, внешние для модели.

Лаговые – переменные, значения которых известны с предыдущего периода

Предопределенные переменные динамической модели – это текущие и лаговые экзогенные, и лаговые эндогенные, стоящие в уравнениях с текущими эндогенными

7. Структурная и приведённая формы спецификации эконометрических моделей. Б. 45, Елисеева

Типы переменных: эндогенные – образуются внутри модели. Экзогенные – не зависят от модели, внешние для модели

Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели, как правило, не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведенная форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели может совпадать с приведенной формой.

Переход от структурной к приведенной форме возможен всегда и однозначно, а обратное _{неверно.}

(более общий и полный вариант нахождения представлен ниже)

Общий вид структурной формы экономической модели имеет вид:

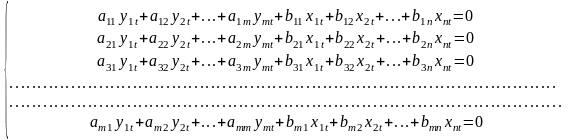
Форма (2.4) называется точечной формой структурной формы экономической модели

Здесь a_ij – параметры, стоящие при эндогенных переменных

b_lj – параметры, стоящие при предопределенных переменных

y_it – эндогенные переменные

x_jt – предопределенные переменные

В канонической (матричной форме) модель имеет вид

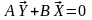
где: A – матрица коэффициентов при эндогенных переменных;

Y – вектор-столбец эндогенных переменных;

B – матрица коэффициентов при предопределенных переменных;

X – вектор столбец предопределенных переменных

Общий вид приведенной формы экономической модели:

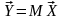
Переход из структурной к приведенной форме модели в общем виде осуществляется:

где: A^-1 –матрица обратная матрице А

А, В – матрицы коэффициентов структурной формы экономической модели

П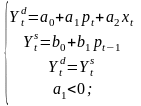 ример. Записать модель конкурентного рынка (2.2) в приведенной форме

1. Выписываем необходимые вектора и матрицы для модели (2.2)

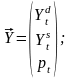
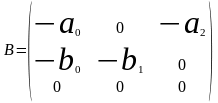
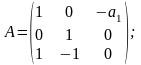
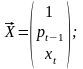
2. Вычисляем матрицу М

Для этого находится обратная матрица А^-1

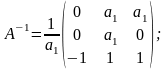
Тогда матрица М есть:

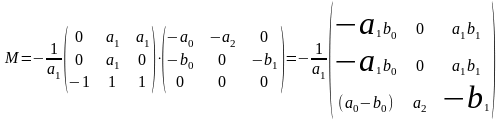
3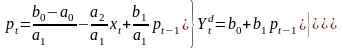 . Приведенная форма модели принимает вид:

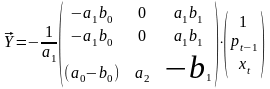
Структурная и приведенная формы модели это две различные формы записи одной модели

8. Отражение в эконометрических моделях фактора времени.

В экономических задачах, для решения которых создаются модели, присутствует фактор времени. Поэтому, он должен быть отражен в спецификации.

Y_t^d – в текущий период Y_t-1^d – в предшествующий период.

Переменные модели называются датированными, если обозначается их зависимость от времени t.

Датирование переменных - третий принцип спецификации эконометрических моделей.

С учетом датирования модель принимает вид динамической модели из одновременных линейных уравнений. Теперь переменные делятся на текущие и лаговые эндогенные и текущие и лаговые экзогенные. Экзогенные (все) и лаговые эндогенные называются предопределенными (т.к. их значения в периоде t известны).

С учетом влияния фактора времени рассмотрим следующие утверждения:

1. Текущий уровень спроса прямо пропорционален текущему доходу(благо ценное), и обратно пропорционален текущей цене(благо нормальное).

2. Текущий уровень предложения прямо пропорционален цене блага в предшествующий момент времени.

3. Текущее значение цены устанавливается при балансе текущих уровней спроса и предложения.

(Система)

y^d_t=a₀ + a₁p_t + a₂x_t

y^s_t =b₀ + b₁p_t-1

y^d_t = y^s_t

a₁ < 0, a₂ >0, b₁ >0

y^d_t , y^s_t , p_t - текущие эндогенные переменные

p_t-1 , x_t – предопределенные переменные

Не во всех ситуациях целесообразно датировать переменные. Если экономические утверждения, на которых базируется спецификация модели, отражают статические взаимосвязи переменных, то надобности в датировании нет. Значения таких переменных называют пространственными данными.

9. Модели временных рядов. К.83-86.+Дарбин-Уотсон, Б.31

Модели, построенные по данным, характеризующим один объект за ряд последова­тельных моментов (периодов) времени второго типа, называются моделями временных рядов.

Временной ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов (периодов времени).

Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент. Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение -мультипликативные модели временного ряда.

Аддитивная модель имеет вид: Y = Т + S + Е; мультипликативная модель: Y=T* S • Е, где Т- тренд, S- сезонная составляющая, Е – случайная составляющая

Модели временных рядов. К этому классу относятся модели:

• тренда: y(t) = T(t) +ξt где t – время; T(t) - временной тренд заданного параметрического вида (например, линейный T(t) = a + bt); ξt - случайная (стохастическая) компонента;

• сезонности: y(t) = S(t) + ξt где S(t) - периодическая (сезонная) компонента, ξt - случайная (стохастическая) компонента.

• тренда и сезонности: y(t) = T(t) + S(t) + ξt (аддитивная) или y(t) = T(t)S{t) + ξt (мультипликативная)

где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента. Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.).

Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д.

Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина – Уотсона:

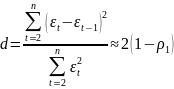
где ρ₁ — коэффициент автокорреляции первого порядка.