30. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений

Дополнение к вопросу 26 Алгоритм проверки значимости регрессора в парной регрессионной модели.

Для оценки статистической значимости коэффициентов регрессии и коэффициента корреляции рассчитывается t-критерий Стьюдента. Выдвигается гипотеза H₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Наблюдаемые значения t-критерия рассчитываются по формулам:

, , ,

(1.7)

где – случайные ошибки параметров линейной регрессии и коэффициента корреляции.

Для линейной парной регрессии выполняется равенство , поэтому проверки гипотез о значимости коэффициента регрессии при факторе и коэффициента корреляции равносильны проверке гипотезы о статистической значимости уравнения регрессии в целом.

Вообще, случайные ошибки рассчитываются по формулам:

, , .

(1.8)

где – остаточная дисперсия на одну степень свободы:

.

(1.9)

Табличное (критическое) значение t-статистики находят по таблицам распределения t-Стьюдента при уровне значимости α = 0,05 и числе степеней свободы Если t_табл < t_факт, то H₀ отклоняется, т.е. коэффициенты регрессии не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора.

Нелинейная модель множественной регрессии (Кобба-Дугласа) Оценка её коэффициентов Линеаризация логарифмированием

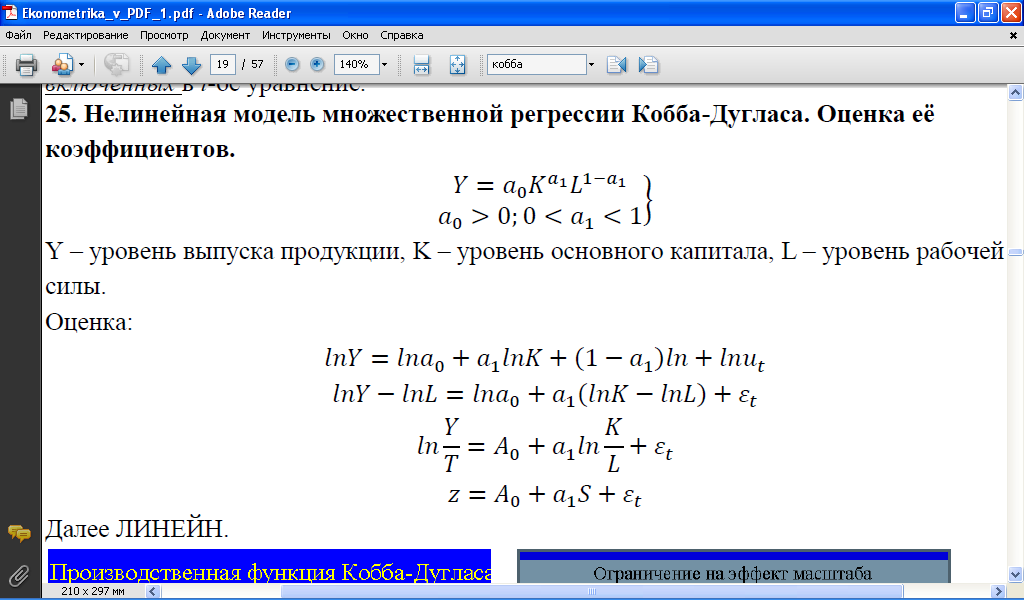
Далее ЛИНЕЙН.

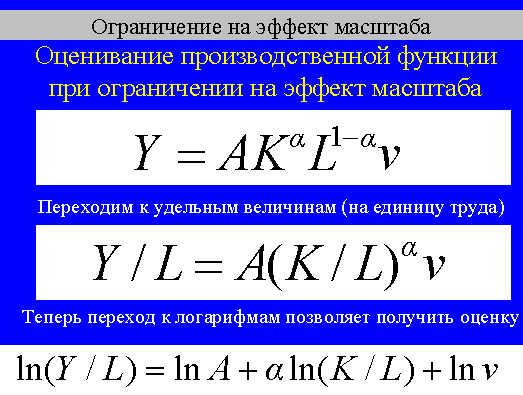
Второй варинат ниже

30. Настройка модели с системой одновременных уравнений

Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими.

Коэффициент уравнения называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он единственный, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.

Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.

Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема.

Уравнение структурной модели может быть идентифицируемо, если выполняется порядковое условие.

Идентифицируемая модель конкурентного рынка

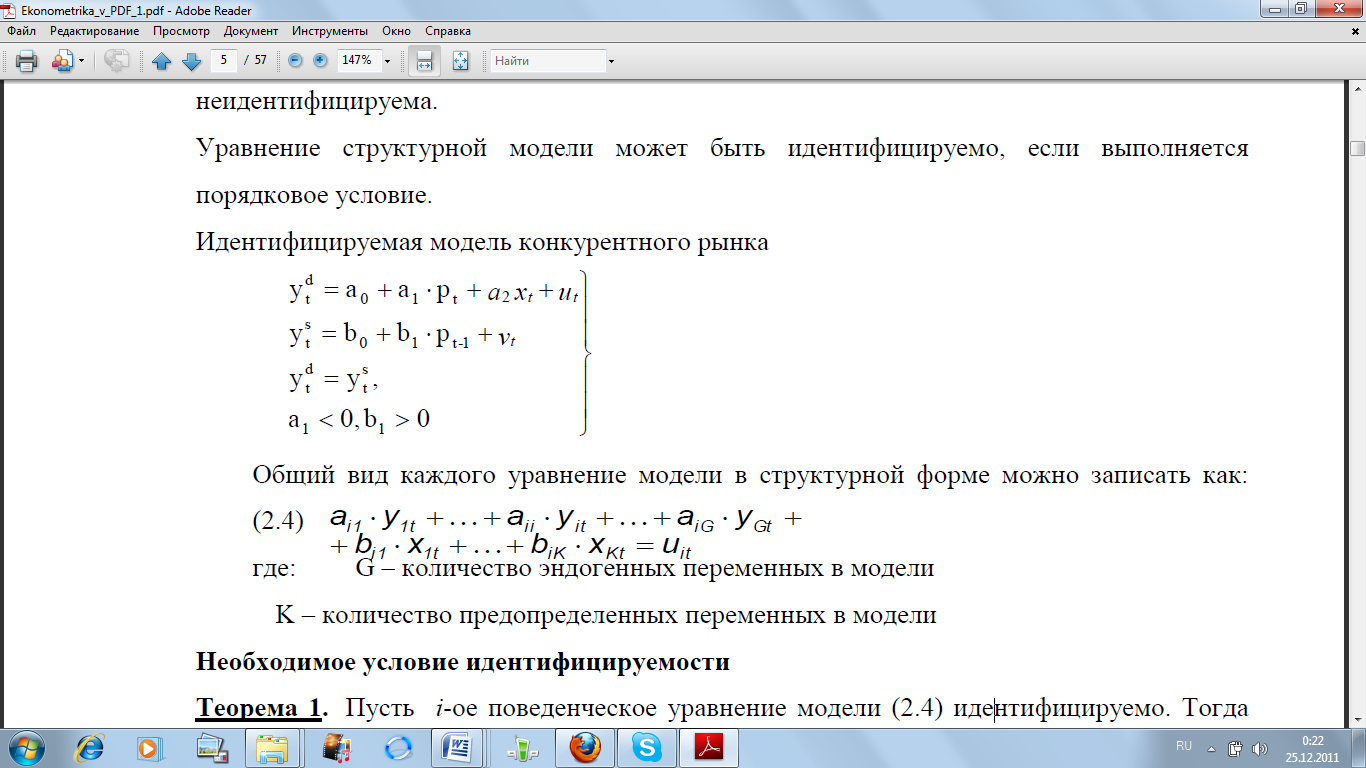
Имеем элементарную модель конкурентного рынка

По результатам наблюдений необходимо получить оценки параметров a0, a1, b0, b1

В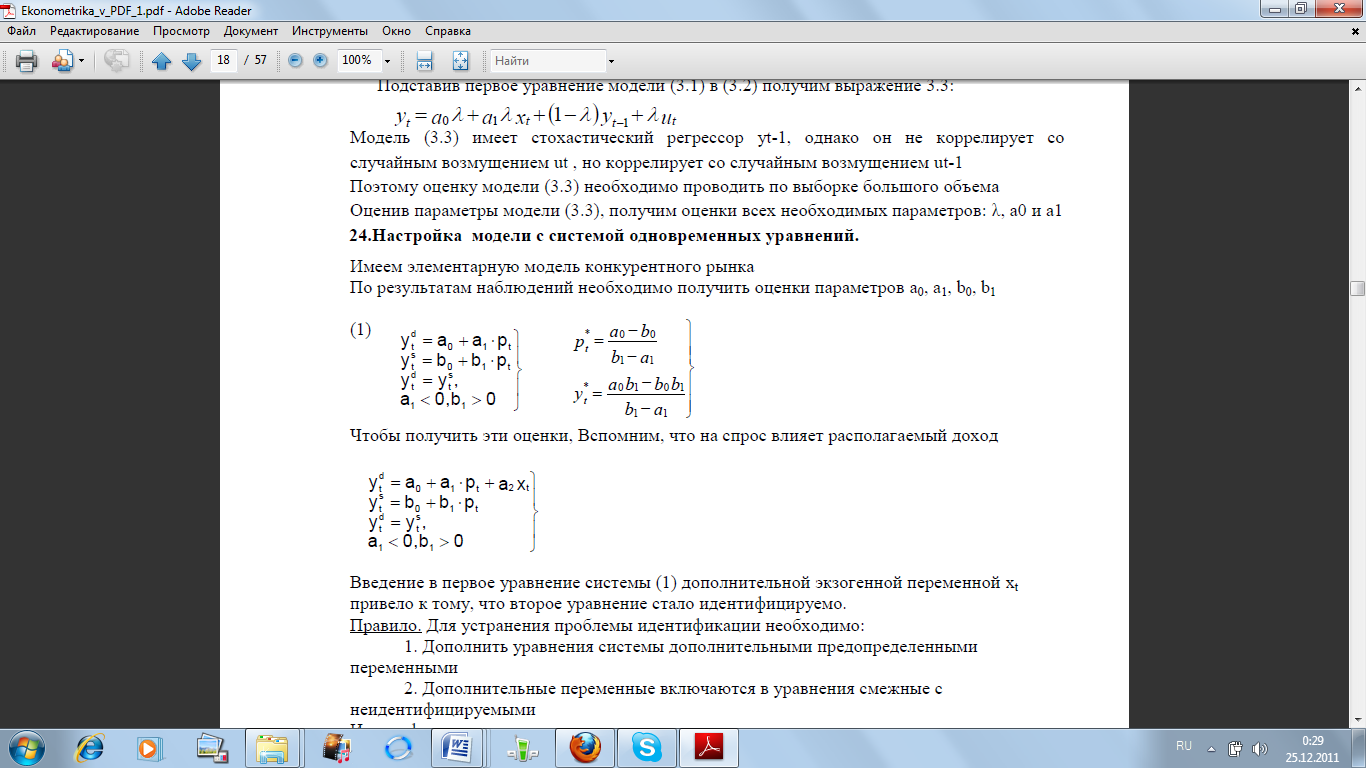 ведение в первое уравнение системы (1) дополнительной экзогенной переменной xt

привело к тому, что второе уравнение стало идентифицируемо.

Правило. Для устранения проблемы идентификации необходимо:

1. Дополнить уравнения системы дополнительными предопределенными переменными

2. Дополнительные переменные включаются в уравнения смежные с неидентифицируемыми

Идентифицируемая модель конкурентного рынка

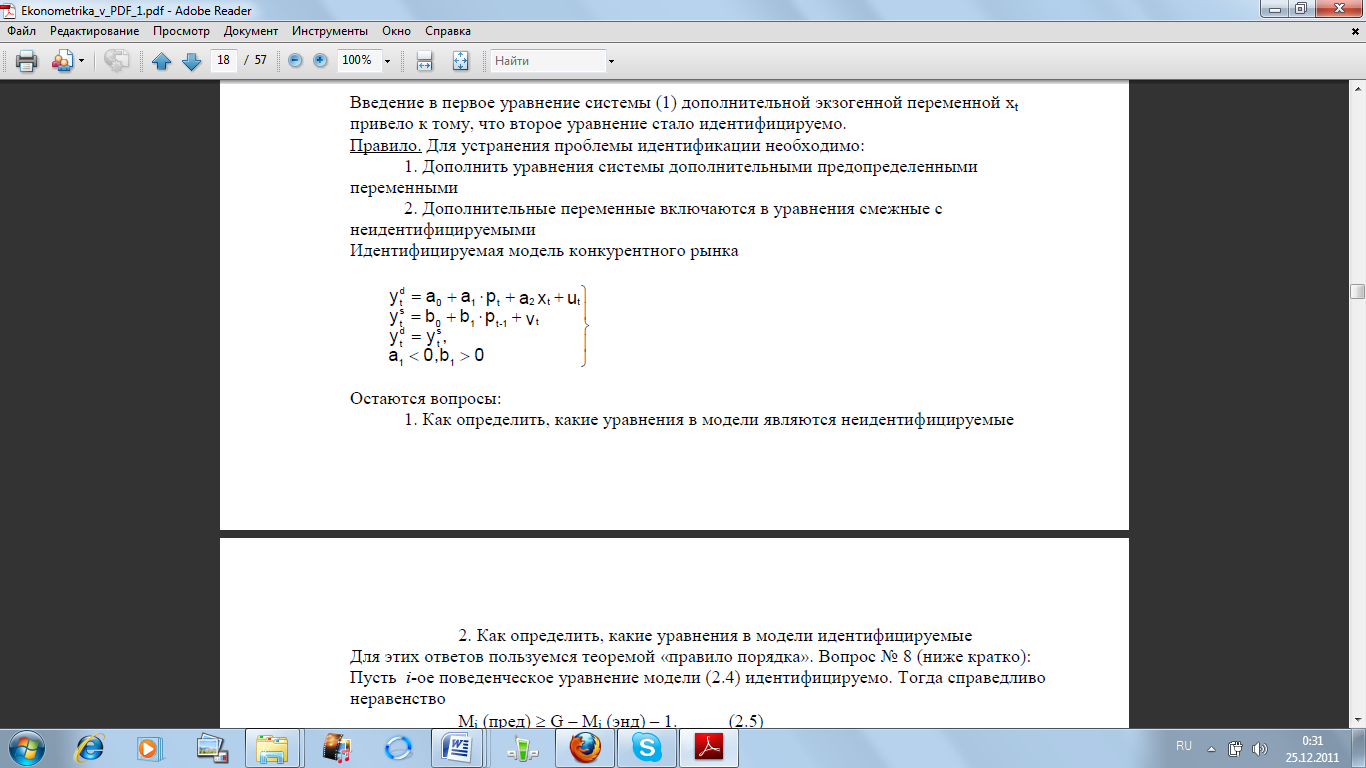
Остаются вопросы:

1. Как определить, какие уравнения в модели являются неидентифицируемые

2. Как определить, какие уравнения в модели идентифицируемые

Для этих ответов пользуемся теоремой «правило порядка».

Пусть i-ое поведенческое уравнение модели идентифицируемо. Тогда справедливо неравенство Mi (пред)  G – Mi (энд) – 1.

В нём:

Mi (пред) – количество предопределённых переменных модели, не включённых в i-ое уравнение; Mi (энд) – количество эндогенных переменных модели, не

включённых в i-ое уравнение.