МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Российский государственный гуманитарный университет» (рггу)

ИНСТИТУТ ИНФОРМАЦИОННЫХ НАУК И ТЕХНОЛОГИЙ

БЕЗОПАСНОСТИ

Факультет защиты информации

Булевы алгебры и их приложения

Реферат

Выполнила:

Жабко Светлана(ФЗИ 2-1)

Москва 2012

Булева алгебра

Булевой алгеброй называется непустое множество A с двумя бинарными операциями   (аналог конъюнкции),   (аналог дизъюнкции), унарной операцией   (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:

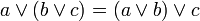
		ассоциативность
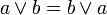
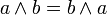
		коммутативность
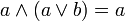
		законы поглощения
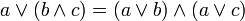
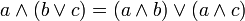
		дистрибутивность
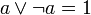
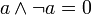
		дополнительность

Первые три аксиомы означают, что (A,  ,  ) является решёткой. Таким образом, булева алгебра может быть определена как дистрибутивная решётка, в которой выполнены две последние аксиомы. Структура, в которой выполняются все аксиомы, кроме предпоследней, называется псевдобулевой алгеброй.

Некоторые свойства

Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:

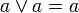
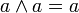
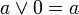
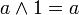
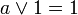
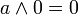
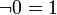
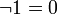
		дополнение 0 есть 1 и наоборот
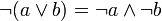
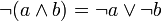
		законы де Моргана
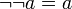.		инволютивность отрицания, закон снятия двойного отрицания.

Основные тождества

В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением ещё нескольких.

Сводная таблица свойств и аксиом, описанных выше:

1. Коммутативность, переместительность:

2. Ассоциативность, сочетательность:

3. Дистрибутивность, распределительность:

   1. конъюнкция относительно дизъюнкции:

2. дизъюнкция относительно конъюнкции:

4. Комплементность, дополнительность(свойства отрицаний):

5. Законы де Моргана: ,

6. Законы поглощения: ,

7. Блейка-Порецкого: ,

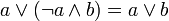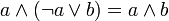
8. Идемпотентность: ,

9. Инволютивность отрицания,закон снятия двойного отрицания:

10. Свойства констант: ,

,

дополнение 0 есть 1  , дополнение 1 есть 0 

11. Склеивание : , Принцип двойственности

В булевых алгебрах существуют двойственные утверждения, они либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула, также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.