
- •1.1.1 Кинематика поступательного движения
- •1) Закон Максвелла о распределении молекул по скоростям
- •6 Билет
- •7 Билет
- •8 Билет.
- •9 Билет
- •10 Билет.
- •Осевые моменты инерции некоторых тел
- •Общие свойства
- •Преобразования Лоренца в физике
- •Законы идеального газа. Изопроцессы.
- •1. Барометрическая формула. Распределение Больцмана.
- •2.Тепловое действие электрического тока.
- •Среднее число столкновений и средняя длина свободного пробега молекул.
- •2.Закон Ома для участка цепи в дифференциальной форме. Удельные сопротивление, проводимость. Плотность тока.
- •2.Плоский воздушный конденсатор. Энергия конденсатора.
- •23.2Теорема Гаусса
10 Билет.
1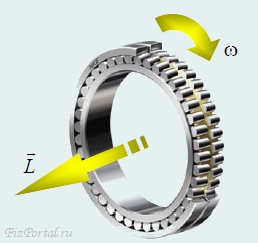 .
Основное уравнение динамики вращательного
движения совпадает с уравнением второго
закона Ньютона для поступательного
движения. Поэтому для описания
вращательного движения можно провести
аналогичные обобщения, приведшие нас
к закону сохранения импульса (рис. 141).
.
Основное уравнение динамики вращательного
движения совпадает с уравнением второго
закона Ньютона для поступательного
движения. Поэтому для описания
вращательного движения можно провести
аналогичные обобщения, приведшие нас
к закону сохранения импульса (рис. 141).
рис. 141
Уравнение динамики вращательного движения тела вокруг неподвижной оси
Iε = M, (1)
где ε = Δω/Δt − угловое ускорение тела, I − его момент инерции, М − сумма моментов внешних сил, действующих на тело, перепишем в виде
Δ(Iω)/Δt = M. (2)
Физическая величина
L = Iω
называется моментом импульса. Уравнение (2) оказывается применимым и для описания вращения тел, момент инерции которых изменяется в процессе движения, поэтому имеет более широкую область применимости, чем уравнение (1). Теперь основное уравнение динамики формулируется так: скорость изменения момента импульса тела равна суммарному моменту сил, действующему на тело. Доказать теоретически это утверждение невозможно − мы провели обобщение, которое подтверждается многочисленными экспериментами. Введенное нами определение момента импульса L = Iω является частным случаем для этой физической величины. Дадим еще одно определение этой физической величины. Пусть материальная точка массы m движется со скоростью v. Импульсом тела называется векторная величина р = mv. Моментом импульса называется произведение импульса тела на плечо импульса (расстояние от оси вращения до прямой, вдоль которой направлен импульс):
L = mvd. (3)
Это определение аналогично определению момента силы. Можно дать эквивалентные выражения формулы (3):
L = mvd = mvrcosα = mvτr,
где r − расстояние от оси вращения до рассматриваемой материальной точки, vτ − составляющая скорости, перпендикулярная радиус-вектору рассматриваемого точечного тела (рис. 142).
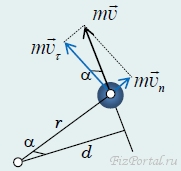
рис. 142
Аналогично
моменту силы момент импульса может быть
определен как векторная физическая
величина, направленная перпендикулярно
плоскости, содержащей вектор импульса mv и
радиус-вектор r.
При таком определении вектор момента
импульса равен векторному произведению
указанных векторов![]() Основное
уравнение динамики вращательного
движения также записывается в векторной
форме:
Основное
уравнение динамики вращательного
движения также записывается в векторной
форме:![]()
Легко показать, что при вращении тела вокруг неподвижной оси из формулы (3) следует выражение для момента импульса L = Iω. Действительно, при вращении вокруг неподвижной оси вектор скорости перпендикулярен прямой, соединяющей точку тела с осью вращения, величина скорости выражается через угловую скорость v = ωr (рис. 143).
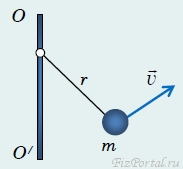
рис. 143
Поэтому момент импульса выражается формулой
L = mvr = mr2ω = mr2ω = Iω,
где I = mr2.
Если же рассмотреть вращение произвольного тела, то для того, чтобы вычислить момент импульса всего тела, достаточно мысленно разбить его на малые части и просуммировать моменты импульсов всех малых частей. Так как угловые скорости всех точек одинаковы, то суммирование сведется к суммированию моментов инерции точек. Легко заметить, что при движении произвольной системы материальных точек изменение суммарного момента импульса полностью определяется моментом внешних сил. По третьему закону Ньютона, тела взаимодействуют с силами, равными по величине и противоположными по направлению. Так как силы взаимодействия направлены вдоль одной прямой, то плечи этих сил равны. Следовательно, при суммировании уравнений вращательного движения для произвольной системы моменты внутренних сил взаимно уничтожатся (подобно тому, как взаимно уничтожаются внутренние силы при сложении уравнений поступательного движения). Таким образом, для произвольной системы материальных точек оказывается справедливым уравнение (3/), в котором М − вектор моментов только внешних сил. Для замкнутой системы тел, не взаимодействующих с другими телами, не включенными в систему, момент внешних сил равен нулю, поэтому для замкнутой системы суммарный момент импульса сохраняется. Это утверждение выражает еще один фундаментальный физический закон − закон сохранения момента импульса. В теоретической физике показано, что он является следствием изотропности1 пространства, в котором происходят все физические явления. Если вы уверены в том, что результаты физического эксперимента одинаковы независимо от того, как ориентирована ваша экспериментальная установка, то вы должны признать закон сохранения импульса.
1Изотропность означает равноправие, одинаковость всех направлений в пространстве.
2. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При
последовательном соединении проводников
сила тока в любых частях цепи одна и та
же: ![]()
Полное
напряжение в цепи при последовательном
соединении, или напряжение на полюсах
источника тока, равно сумме напряжений
на отдельных участках цепи: ![]()
Резисторы
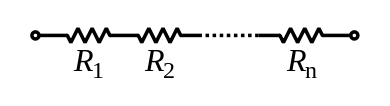
![]()
Катушка индуктивности
![]()
![]()
Электрический конденсатор
![]()
![]()
.
Мемристоры
![]()
Параллельное соединение
Сила
тока в неразветвленной части цепи равна
сумме сил токов в отдельных параллельно
соединённых проводниках: ![]()
Напряжение
на участках цепи АВ и на концах всех
параллельно соединённых проводников
одно и то же: ![]()
Резистор
При
параллельном соединении резисторов
складываются величины, обратно
пропорциональные сопротивлению (то
есть общая проводимость ![]() складывается
из проводимостей каждого резистора
складывается
из проводимостей каждого резистора ![]() )
)
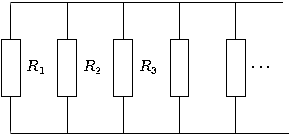
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее(искомое) сопротивление.
Доказательство:
Д![]() ля
двух параллельно соединённых резисторов
их общее сопротивление равно:
ля
двух параллельно соединённых резисторов
их общее сопротивление равно: ![]() .
.
Если ![]() ,
то общее сопротивление равно:
,
то общее сопротивление равно: ![]()
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
Катушка индуктивности
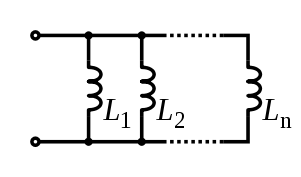
Билет 11
1 Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведениюрадиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Формула момента рычага

![]()
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
![]() = МОМЕНТ_РЫЧАГА
* СИЛА
= МОМЕНТ_РЫЧАГА
* СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
![]() = РАССТОЯНИЕ_ДО_ЦЕНТРА
* СИЛА
= РАССТОЯНИЕ_ДО_ЦЕНТРА
* СИЛА
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
![]() ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
![]() ,
,
То есть, если I постоянная, то
![]() ,где
α — угловое
ускорение,
измеряемое в радианах в секунду за
секунду.
,где
α — угловое
ускорение,
измеряемое в радианах в секунду за
секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
![]() = МОМЕНТ_СИЛЫ
* УГЛОВАЯ_СКОРОСТЬ
= МОМЕНТ_СИЛЫ
* УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
![]() = МОМЕНТ_СИЛЫ
* УГОЛ
= МОМЕНТ_СИЛЫ
* УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно
известна угловая скорость ![]() в
радианах в секунду и время действия
МОМЕНТА
в
радианах в секунду и время действия
МОМЕНТА ![]() .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
= МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
Если
имеется материальная точка ![]() ,
к которой приложена сила
,
к которой приложена сила ![]() ,
то момент силы относительно точки
,
то момент силы относительно точки ![]() равен
векторному произведению радиус-вектора
равен
векторному произведению радиус-вектора ![]() ,
соединяющего точки
и
,
соединяющего точки
и ![]() ,
на вектор силы
:
,
на вектор силы
:
![]() .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивныхдатчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
|
Особенности вращательного движения твердого тела под действием внешних сил. Опыт показывает, что при вращательном движении твердого тела вокруг закрепленной оси масса уже не является мерой его инертности, а сила - недостаточна для характеристики внешнего воздействия. Пример. Маятник Обербека. Ускорение при вращательном движении зависит: - не только от массы тела, но и от ее распределения относительно оси вращения, - не только от силы, но и от точки ее приложения и направления действия. Таким образом для описания вращательного движения твердого тела необходимо ввести новые характеристики. Момент силы, действующей на материальную точку. Пусть частицаA движется произвольным образом относительно точки О под действием силы F (см. рис. 6.2). Моментом силы частицы относительно закрепленной точки называется величина, равная векторному произведению: M = [r·F], (6.3) где r - радиус вектор точки приложения силы F.
|
||||||
|
Момент силы - векторная величина. Для нахождения ее направления вектора r и F необходимо изобразить исходящими из одной точки и связать с ними правый винт (см. рис. 6.3). Затем головку правого винта нужно вращать от r к F. Направление движения винта будет совпадать с векторомM. Величина вектора момента сил равна: M = r·F·sin() = F·R, (6.4) где R = r·sin() - плечо силы, равное кратчайшему расстоянию между осью вращения и линией действия силы (см. рис. 6.2). |
||||||
|
Момент силы относительно оси вращения. Моментом силы относительно произвольной оси Z, проходящей через точку О, в которой закреплено твердое тело, называется величина, равная проекции вектора Mна эту ось. Mz = [r·F]z. Найдем значение момента сил для твердого тела, вращающегося вокруг закрепленной оси Z под действием силы F (см. рис. 6.4). Разложим эту силу на три составляющие: F = F|| + F + Fn, где F|| - составляющая силы, параллельная оси вращения, F - тангенциальная составляющая силы, расположенная в плоскости вращения, Fn - нормальная составляющая силы, расположенная в плоскости вращения. Момент силы относительно точки О можно представить как векторную сумму моментов, созданных этими силами: M = M|| + M + Mn. Моменты M|| и Mn перпендикулярны оси вращения и их проекции на эту ось равны нулю. Момент силы Mобразует с ней угол . Таким образом, проекция результирующего момента на ось Z равна (см. рис. 6.4): Mz = Mz = |M|·cos(=r·F·cos(= R·F. |
||||||
|
Из опыта следует, что только сила F способна вызвать вращение тела вокруг закрепленной оси. Чем дальше от оси расположена точка приложения тангенциальной составляющей силы, тем легче осуществить поворот. Следовательно, момент силы относительно оси характеризует способность силы вращать тело относительно данной оси. Момент силы M относительно точки, в которой закреплено тело, характеризует способность силы вращать тело вокруг точки, относительно которой он берется. Причем поворот произойдет вокруг оси, параллельной вектору момента сил M. При вращательном движении силовое воздействие характеризуется моментом силы, а не силой.
|
||||||
|
Момент инерции. Моментом инерции материальной точки массы mотносительно оси называется величина, равная: I = m·r2, (6.5) где r - кратчайшее расстояние от оси вращения до точки. Момент инерции твердого тела равен сумме моментов инерции его частей: I = mi·ri2 (6.6) Следовательно, момент инерции твердого тела зависит от:
Для симметричных тел момент инерции рассчитывается с помощью интегрального исчисления. Моменты инерции некоторых симметричных тел приведены в таблице.
|
||||||
|
Динамика вращательного движения материальной точки.Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F (см. рис. 6.5). В инерциальной системе отсчета справедлив 2ой закон Ньютона. Запишем его применительно к произвольному моменту времени: F = m·a. Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид: F= m·a. Поскольку a = ·R, то F= m··R(6.6) Умножив левую и правую части уравнения скалярно на R, получим: F·R= m··R2 (6.7) M = I· (6.8) Уравнение (6.8) представляет собой 2ой закон Ньютона (уравнение динамики) для вращательного движения материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора углового ускорения, направленного вдоль оси вращения (см. рис. 6.5): M = I·(6.9) Основной закон динамики материальной точки при вращательном движении можно сформулировать следующим образом: произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.
|
||||||
|
Закон динамики вращательного движения твердого тела. Обобщим полученный результат для твердого тела. Разобьем тело на элементарные участки массой mi. Пусть ri - расстояние от оси вращения до элемента массойmi, а Ii - его момент инерции. Обозначим за Mi результирующий момент внешних сил, действующий на элемент mi, а Mi* - результирующий момент внутренних сил, действующий на него со стороны других элементов тела. Из уравнения (6.9) следует, что: Mi + Mi* = Ii·(6.10) где Ii - момент инерции элементарного участка тела относительно оси вращения. Просуммировав уравнения (6.10) по всем элементам, и учитывая, что согласно 3ему закону Ньютона суммарный момент внутренних сил равен нулю, получим уравнение, аналогичное (6.9): M = I·(6.11) где M - суммарный момент внешних сил, действующих на твердое тело, относительно закрепленной точки О; I - момент инерции тела относительно оси вращения. Следовательно, основной закон динамики вращательного движения твердого тела относительно закрепленной точки можно сформулировать следующим образом: произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение. В случае движения тела относительно закрепленной оси необходимо спроецировать уравнение (6.11) на эту ось. Mz = Iz·. (6.12) Из уравнения (6.12) можно найти какое угловое ускорение относительно закрепленной оси приобретет тело под действием момента сил Mz.
|
||||||
|
Условия равновесия твердого тела. Тело находится в равновесии, если оно не обладает ускорением поступательного и вращательного движений, т.е. выполняются следующие условия: a = 0, = 0. Очевидно, что это имеет место при равенстве нулю результирующей силы и суммарного момента внешних сил. Следовательно, в условии равновесия выполняются равенства: F = 0 и M = 0. |
||||||
|
Заметим, что равенство нулю результирующего вектора сил, действующих на тело, не обязательно обуславливает равенство нулю суммарного момента внешних сил. Типичным примером является момент пары сил, вызывающего движение тела с угловым ускорением (см. рис. 6.6). Расстояние между линиями продолжения сил l называется плечом пары. Момент пары сил равен: M = [R12·F], где R12 - вектор расстояния между точками приложения сил. Абсолютное значение момента пары сил равно: |M| = l·F.
|
2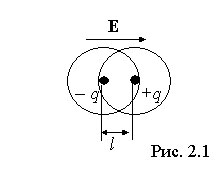
Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля
Индуцированный
дипольный момент молекулы пропорционален
напряженности внешнего электрического
поля ![]() ,
где
,
где ![]() -
поляризуемость молекулы. Значение
поляризованности в этом случае равно
-
поляризуемость молекулы. Значение
поляризованности в этом случае равно ![]() ,
где n -
концентрация молекул
,
где n -
концентрация молекул ![]() ;
; ![]() -
индуцированный дипольный момент
молекулы, который одинаков для всех
молекул и направление которого совпадает
с направлением внешнего поля.
Ориентационнный
тип поляризации характерен
для полярных диэлектриков. В отсутствие
внешнего электрического поля молекулярные
диполи ориентированы случайным образом,
так что макроскопический электрический
момент диэлектрика равен нулю.
-
индуцированный дипольный момент
молекулы, который одинаков для всех
молекул и направление которого совпадает
с направлением внешнего поля.
Ориентационнный
тип поляризации характерен
для полярных диэлектриков. В отсутствие
внешнего электрического поля молекулярные
диполи ориентированы случайным образом,
так что макроскопический электрический
момент диэлектрика равен нулю.
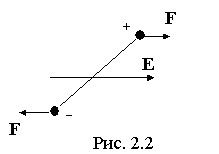
Если
поместить такой диэлектрик во внешнее
электрическое поле, то на молекулу-диполь
будет действовать момент сил (рис. 2.2),
стремящийся ориентировать ее дипольный
момент в направлении напряженности
поля. Однако полной ориентации не
происходит, поскольку тепловое движение
стремится разрушить действие внешнего
электрического поля.
Такая
поляризация называется ориентационной.
Поляризованность в этом случае равна ![]() ,
где <p>
- среднее значение составляющей дипольного
момента молекулы в направлении внешнего
поля.
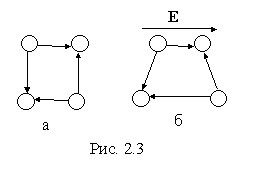
Решеточный
тип поляризации характерен
для ионных кристаллов. В ионных кристаллах
(NaCl и т.д.) в отсутствие внешнего поля
дипольный момент каждой элементарной
ячейки равен нулю (рис. 2.3.а), под влиянием
внешнего электрического поля положительные
и отрицательные ионы смещаются в
противоположные стороны (рис. 2.3.б).
Каждая ячейка кристалла становится
диполем, кристалл поляризуется. Такая
поляризация называется решеточной.
Поляризованность и в этом случае можно
определить как
,
где <p>
- среднее значение составляющей дипольного
момента молекулы в направлении внешнего
поля.
Решеточный
тип поляризации характерен
для ионных кристаллов. В ионных кристаллах
(NaCl и т.д.) в отсутствие внешнего поля
дипольный момент каждой элементарной
ячейки равен нулю (рис. 2.3.а), под влиянием
внешнего электрического поля положительные
и отрицательные ионы смещаются в
противоположные стороны (рис. 2.3.б).
Каждая ячейка кристалла становится
диполем, кристалл поляризуется. Такая
поляризация называется решеточной.
Поляризованность и в этом случае можно
определить как ![]() ,
где
-
значение дипольного момента элементарной
ячейки, n -
число ячеек в единице объема.
,
где
-
значение дипольного момента элементарной
ячейки, n -
число ячеек в единице объема.
Поляризованность
изотропных диэлектриков любого типа
связана с напряженностью поля
соотношением ![]() ,
где
,
где ![]() - диэлектрическая
восприимчивость диэлектрика.
- диэлектрическая
восприимчивость диэлектрика.
Напряженность поля в диэлектрике
Рассмотрим
диэлектрическую пластинку, заполняющую
плоский конденсатор (рис.14.5) и находящуюся,
следовательно, в практически однородном
внешнем поле ![]() .
.
В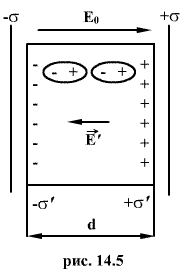 результате поляризации на гранях
диэлектрика, обращенных к пластинам
конденсатора, концы молекулярных диполей
окажутся нескомпенсированными соседними
диполями. Поэтому на правой грани,
обращенной к отрицательной пластине
конденсатора, окажется избыток
положительного заряда с некоторой
поверхностной плотностью
результате поляризации на гранях
диэлектрика, обращенных к пластинам
конденсатора, концы молекулярных диполей
окажутся нескомпенсированными соседними
диполями. Поэтому на правой грани,
обращенной к отрицательной пластине
конденсатора, окажется избыток
положительного заряда с некоторой
поверхностной плотностью ![]() .
На противоположной стороне диэлектрика
.
На противоположной стороне диэлектрика ![]() .
Эти так называемые поляризационные,
или связанные заряды не могут быть
переданы соприкосновением другому телу
без разрушения молекул диэлектрика,
т.к. они обусловлены самими поляризованными
молекулами. Возникновение поляризованных
зарядов приводит к возникновению
дополнительного электрического поля
.
Эти так называемые поляризационные,
или связанные заряды не могут быть
переданы соприкосновением другому телу
без разрушения молекул диэлектрика,
т.к. они обусловлены самими поляризованными
молекулами. Возникновение поляризованных
зарядов приводит к возникновению
дополнительного электрического поля ![]() ,
направленного против внешнего поля
.
Результирующее электрическое поле Е
внутри диэлектрика равно
,
направленного против внешнего поля
.
Результирующее электрическое поле Е
внутри диэлектрика равно
|
(14.2) |
Для
определения ![]() применим
формулу вычисления напряженности
применим
формулу вычисления напряженности ![]() конденсатора
конденсатора
|
(14.3) |
Свяжем ![]() с
вектором поляризации Р. Для этого
определим полный дипольный момент (во
всем объеме) диэлектрика. Осуществим
это двумя способами:
с
вектором поляризации Р. Для этого
определим полный дипольный момент (во
всем объеме) диэлектрика. Осуществим
это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
|
(14.4) |
где S - площадь пластины конденсатора.
С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряд , а с другой и расстояние d. Отсюда
|
(14.5) |
Приравнивая (14.4) и (14.5), получим
![]()
Подставляя в (14.3), и затем результат в (14.2), получим
![]()
Подставим значение Р из выражения (14.1), тогда
|
(14.6) |
Величина
|
(14.7) |
называется
диэлектрической проницаемостью или
относительной диэлектрической
проницаемостью. Диэлектрическая
проницаемость ![]() показывает
во сколько раз уменьшается напряженность
в диэлектрике по сравнению с напряженностью
в вакууме.
показывает
во сколько раз уменьшается напряженность
в диэлектрике по сравнению с напряженностью
в вакууме. ![]() и
и ![]() ,
т.е. с ростом температуры диэлектрические
свойства ухудшаются.
,
т.е. с ростом температуры диэлектрические
свойства ухудшаются.
Билет 12
1Момент инерции — скалярная физическая величина, мера инертности во вращательном движениивокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,
,
где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
![]() ,
,
где:
![]() —
масса
малого элемента объёма тела
—
масса
малого элемента объёма тела ![]() ,
,
![]() —
плотность,
—
плотность,
![]() —
расстояние
от элемента
до
оси a.
—
расстояние
от элемента
до
оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
![]()
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела Jотносительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масстела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
![]() ,
,
где ![]() —
полная масса тела.
—
полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
![]()

 Рис.
6.2.
Рис.
6.2.  Рис.
6.3.
Рис.
6.3. Рис.
6.4.
Рис.
6.4.
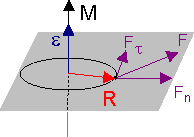 Рис.
6.5.
Рис.
6.5.
 Рис.
6.6.
Рис.
6.6.