
- •1.1.1 Кинематика поступательного движения
- •1) Закон Максвелла о распределении молекул по скоростям
- •6 Билет
- •7 Билет
- •8 Билет.
- •9 Билет
- •10 Билет.
- •Осевые моменты инерции некоторых тел
- •Общие свойства
- •Преобразования Лоренца в физике
- •Законы идеального газа. Изопроцессы.
- •1. Барометрическая формула. Распределение Больцмана.
- •2.Тепловое действие электрического тока.
- •Среднее число столкновений и средняя длина свободного пробега молекул.
- •2.Закон Ома для участка цепи в дифференциальной форме. Удельные сопротивление, проводимость. Плотность тока.
- •2.Плоский воздушный конденсатор. Энергия конденсатора.
- •23.2Теорема Гаусса
23.2Теорема Гаусса
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем
новую физическую величину, характеризующую
электрическое поле – поток Φ вектора
напряженности электрического поля.
Пусть в пространстве, где создано
электрическое поле, расположена некоторая
достаточно малая площадка ΔS. Произведение
модуля вектора
![]() на
площадь ΔS и на косинус угла α между
вектором
и
нормалью
на
площадь ΔS и на косинус угла α между
вектором
и
нормалью
![]() к
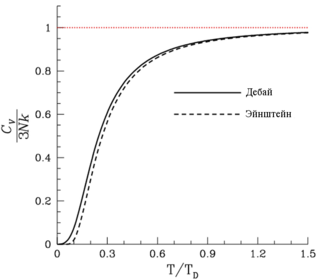
площадке называется элементарным
потоком вектора напряженности через
площадку ΔS (рис. 1.3.1):
к
площадке называется элементарным
потоком вектора напряженности через
площадку ΔS (рис. 1.3.1):
ΔΦ = E ΔS cos α = En ΔS, |
где
En
– модуль нормальной составляющей поля
![]()
|
Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
|
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
|
Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
|
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
|
где
R – радиус сферы. Поток Φ через сферическую
поверхность будет равен произведению
E на площадь сферы 4πR2.
Следовательно,

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 1.3.3).
|
Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS '. |
Здесь ΔS' = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так
как
![]() а
а
![]() следовательно
следовательно
![]() Отсюда
следует, что полный поток электрического
поля точечного заряда через произвольную
поверхность, охватывающую заряд, равен
потоку Φ0
через поверхность вспомогательной
сферы:
Отсюда
следует, что полный поток электрического
поля точечного заряда через произвольную
поверхность, охватывающую заряд, равен
потоку Φ0
через поверхность вспомогательной
сферы:
|
Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение
теоремы Гаусса на случай произвольного
распределения зарядов вытекает из
принципа суперпозиции. Поле любого
распределения зарядов можно представить
как векторную сумму электрических полей
![]() точечных
зарядов. Поток Φ системы зарядов через
произвольную замкнутую поверхность S
будет складываться из потоков Φi
электрических полей отдельных зарядов.
Если заряд qi
оказался внутри поверхности S, то он
дает вклад в поток, равный
точечных
зарядов. Поток Φ системы зарядов через
произвольную замкнутую поверхность S
будет складываться из потоков Φi
электрических полей отдельных зарядов.
Если заряд qi
оказался внутри поверхности S, то он
дает вклад в поток, равный
![]() если
же этот заряд оказался снаружи поверхности,
то вклад его электрического поля в поток
будет равен нулю.
если
же этот заряд оказался снаружи поверхности,
то вклад его электрического поля в поток
будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
|
Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. OO' – ось симметрии |
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
|
где τ – заряд единицы длины цилиндра. Отсюда
|
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
|
Рисунок 1.3.5.Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:
|
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
Билет 24.1
Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
где
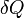 —
подведённое
к телу количество теплоты, измеренное
в джоулях
—
подведённое
к телу количество теплоты, измеренное
в джоулях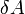 [1] —
работа,
совершаемая телом против внешних сил,
измеренная в джоулях
[1] —
работа,
совершаемая телом против внешних сил,
измеренная в джоулях
Эта формула является математическим выражением первого начала термодинамики
Для квазистатических процессов выполняется следующее соотношение:
![]()
где
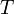 —
температура,
измеренная в кельвинах
—
температура,
измеренная в кельвинах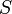 —
энтропия,
измеренная в джоулях/кельвин
—
энтропия,
измеренная в джоулях/кельвин —
давление,
измеренное в паскалях
—
давление,
измеренное в паскалях —
химический
потенциал
—
химический
потенциал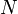 —
количество
частиц в системе
—
количество
частиц в системе
Идеальные газы
Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа
не зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости
при постоянном объёме,
![]() .
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
.
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
![]() .
.
Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае
![]() является
функцией и температуры, и объёма.
является
функцией и температуры, и объёма.
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
![]() ,
,
где
![]() —
количество вещества,
—
количество вещества,
![]() —
изменение температуры.
—
изменение температуры.
числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения. В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.
Рис.1
 При
любом числе степеней свободы данной
молекулы три степени свободы всегда
поступательные. Ни одна из поступательных
степеней свободы не имеет преимущества
перед другими, значит на каждую из них
приходится в среднем одинаковая энергия,
равная 1/3 значения <ε0>
(энергия поступательного движения
молекул):
При
любом числе степеней свободы данной
молекулы три степени свободы всегда
поступательные. Ни одна из поступательных
степеней свободы не имеет преимущества
перед другими, значит на каждую из них
приходится в среднем одинаковая энергия,
равная 1/3 значения <ε0>
(энергия поступательного движения
молекул):
![]() В
статистической физике выводится закон
Больцмана о равномерном распределении
энергии по степеням свободы молекул:
для статистической системы, которая
находится в состоянии термодинамического
равновесия, на каждую поступательную
и вращательную степени свободы приходится
в среднем кинетическая энергия, равная
kT/2, а на каждую колебательную степень
свободы — в среднем энергия, равная kT.
Колебательная степень обладает вдвое
большей энергией, т.к. на нее приходится
как кинетическая энергия (как в случае
поступательного и вращательного
движений), так и потенциальная, причем
средние значения потенциальной и
кинетической и энергии одинаковы.
Значит, средняя энергия молекулы
В
статистической физике выводится закон
Больцмана о равномерном распределении
энергии по степеням свободы молекул:
для статистической системы, которая
находится в состоянии термодинамического
равновесия, на каждую поступательную
и вращательную степени свободы приходится
в среднем кинетическая энергия, равная
kT/2, а на каждую колебательную степень
свободы — в среднем энергия, равная kT.
Колебательная степень обладает вдвое
большей энергией, т.к. на нее приходится
как кинетическая энергия (как в случае
поступательного и вращательного
движений), так и потенциальная, причем
средние значения потенциальной и
кинетической и энергии одинаковы.
Значит, средняя энергия молекулы
![]() где
i
— сумма числа поступательных, числа
вращательных в удвоенного числа
колеба¬тельных степеней свободы
молекулы: i=iпост+iвращ+2iколеб
В классической теории рассматривают
молекулы с жесткой связью между атомами;
для них i
совпадает с числом степеней свободы
молекулы.
Так как в идеальном
газе взаимная потенциальная энергия
взаимодействия молекул равна нулю
(молекулы между собой не взаимодействуют),
то внутренняя энергия для одного моля
газа, будет равна сумме кинетических
энергий NA
молекул:
где
i
— сумма числа поступательных, числа
вращательных в удвоенного числа
колеба¬тельных степеней свободы
молекулы: i=iпост+iвращ+2iколеб
В классической теории рассматривают
молекулы с жесткой связью между атомами;
для них i
совпадает с числом степеней свободы
молекулы.
Так как в идеальном
газе взаимная потенциальная энергия
взаимодействия молекул равна нулю
(молекулы между собой не взаимодействуют),
то внутренняя энергия для одного моля
газа, будет равна сумме кинетических
энергий NA
молекул:
![]() (1)
Внутренняя энергия для произвольной
массы m газа.
(1)
Внутренняя энергия для произвольной
массы m газа.
![]() где
М — молярная масса, ν
— количество вещества.
где
М — молярная масса, ν
— количество вещества.
24.2
Электрический ток. Условия необходимые для возникновения и существования электрического тока.
Е сли
к изолированному проводнику приложить
электрическое поле
сли
к изолированному проводнику приложить
электрическое поле
![]() ,
то на свободные заряды q
в проводнике будет действовать сила
,
то на свободные заряды q
в проводнике будет действовать сила
![]() =q
.
В результате в проводнике возникает
упорядоченное перемещение свободных
зарядов, возникает электрический ток.
=q
.
В результате в проводнике возникает
упорядоченное перемещение свободных
зарядов, возникает электрический ток.
Непрерывное упорядоченное движение свободных носителей электрического заряда называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов.
Условия, необходимые для существования электрического тока:
наличие свободных заряженных частиц;
наличие электрического поля;
– замкнутость цепи.
Действие тока, сопровождающие его протекание:
Тепловое. Проводник, по которому течет ток, нагревается. Тепловое действие проявляется практически всегда. Исключение составляет явление сверхпроводимости, тепловое действие тока не проявляется также при протекании тока в вакууме.
Химическое. Электрический ток изменяет химический состав проводника. Наблюдается при протекании тока в электролитах.
Магнитное. Ток оказывает силовое воздействие на соседние токи и на магнитные тела. Магнитное воздействие на соседние точки и на магнитные тела. Магнитное действие в отличие от химического и от теплового явления является основным, так как проявляется у всех без исключения проводников(наблюдается всегда).
Электрический ток всегда в проводниках (металлах) обусловлен наличием свободных электронов.
Положительно заряженные ионы металла образуют кристаллическую решетку. “Газ свободных электронов” образуется за счет одного или нескольких электронов, отданных каждым атомом. Свободные электроны способны блуждать по всему объему кристалла.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Силой тока называется скалярная физическая величина, численно равная электрическому заряду, проходящему через поперечное сечение проводника за единицу времени:
I=![]() .
.
Если
величина силы тока и его направление
не меняются с течением времени, то ток
называется постоянным и I=const=![]() .
.
Единица силы тока-1 Ампер. Ампер в системе СИ является основной единицей и определяется из магнитного взаимодействия двух параллельных прямолинейных проводников, по которым в одном направлении течёт ток силой 1 А, расположенных на расстоянии 1 м один от другого в вакууме, вызывает между этими проводниками силу взаимодействия, равную 2*10-7 Н на каждый метр длины.
Сила тока зависит от заряда частицы e, концентрации n, скорости частиц v и площади сечения проводника S:
I=
=![]() =
=![]() ,
где q=eN;
n-концентрация частиц; V=vtS
содержится N=nV
частиц.
,
где q=eN;
n-концентрация частиц; V=vtS
содержится N=nV
частиц.
Плотностью
тока
![]() называется
векторная величина, численно равная
силе тока, приходящегося на единицу
площади, ориентированной перпендикулярно
току:
называется
векторная величина, численно равная
силе тока, приходящегося на единицу
площади, ориентированной перпендикулярно
току:
![]() .
.
Вектор
j
направлен вдоль тока по вектору
напряженности электрического поля в
проводнике. В системе СИ плотность тока
измеряется в А/м2
. Для
постоянного тока
![]()
Билет 25.1
Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Первое начало термодинамики |
В термодинамике широко используются понятия молярной теплоемкости при постоянном объеме CV и молярной теплоемкости при постоянном давлении Cp. В идеальном газе они удовлетворяют уравнению Майера:
Cp – CV = R. |
Теплоемкость
одного моля одноатомного идеального
газа при постоянном объеме равна
![]() ,
двухатомного –
,
двухатомного –
![]() ,
многоатомного – 3R.
,
многоатомного – 3R.
Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре:
U = CVT. |
Работа ΔA, совершаемая газом, определяется давлением газа и изменением его объема:
ΔA = pΔV. |
|
Рисунок 2.3.1. Если давление газа в процессе совершения работы изменяется, то работа может быть найдена по площади под графиком. |
|
Рисунок 2.3.2. Работа газа зависит от пути, по которому газ переходит из состояния 1 в состояние 2. |
Первое начало термодинамики. Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и на совершение работы над внешними телами:
Q = ΔU + A. |
В изохорном процессе газ работы не совершает, и ΔU = Q. В изобарном процессе A = pΔV = p (V2 – V1). В изотермическом процессе ΔU = 0, и A = Q; вся теплота, переданная телу, идет на работу над внешними телами. Графически работа равна площади под кривой процесса на плоскости p, V.
|
Рисунок 2.3.3. Первое начало термодинамики для изохорного процесса. |
|
Рисунок 2.3.4. Первое начало термодинамики для изобарного процесса. |
|
Рисунок 2.3.5. Первое начало термодинамики для изотермического процесса. |
|
Рисунок 2.3.6. Первое начало термодинамики для адиабатного процесса. |
Адиабатным называется квазистатический процесс, при котором системе не передается тепло из окружающей среды: Q = 0. В адиабатном процессе вся работа совершается за счет внутренней энергии газа.
Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT:
![]()
Единица измерения теплоёмкости в системе СИ — Дж/К.
Удельная теплоёмкость
Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.
Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).
Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).
Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)).
Теплоёмкость для различных состояний вещества
Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).
Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:
![]()
где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная.
А при постоянном давлении
![]()
Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).
Т
 еория
теплоёмкости
еория
теплоёмкости
Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела
Существует несколько теорий теплоёмкости твердого тела:
Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).
Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.
Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.
Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.
Работа при изменении объема газа |
|
|
Газ оказывает давление на любую стенку сосуда. Если стенка подвижна (например, поршень на рис. 1), то сила давления F совершит работу A, переместив поршень на расстояние L. Если L невелико, то давление газа останется примерно постоянным. Тогда работа будет равна: A = F·L·cos= P·S·L, где S - площадь поршня, - угол между направлением силы и перемещением поршня (= 0). Произведение S·L равно изменению объема газа V от начального V1 до конечного V2 значения, т.е. S·L =V = V1 - V2. Тогда A = P·(V2 - V1) = P·V. В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа на поршень будет постоянной, и формула работы сохранит свой вид A = P·(V2 - V1). |
|
|
Как видно из рисунка 2, работа газа при изобарном расширении равна площади под графиком процесса в координатах P, V. |
|
|||||||||||||||||||||
Если в процессе расширения давление газа изменяется, то для вычисления работы можно воспользоваться графическим методом (см. рис. 3). Пусть процесс расширения имеет вид, изображенный на рисунке. При любом малом изменении объема V работа равна площади малого прямоугольника (на рис. 3 он заштрихован). Полная работа равна сумме площадей всех малых прямоугольников и равна площади фигуры, ограниченной линией, представляющей собой график процесса.
|
|
|||||||||||||||||||||
При сжатии газа внешними силами перемещение поршня L противоположно силе давления газа F, тогда работа газа будет отрицательной величиной (V < 0). Работа внешней силы A' в данном случае будет положительной, а величина A' = - A. Работа газа в циклических процессах Совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние называется циклом. Все тепловые машины (двигатели внутреннего сгорания, холодильные и паровые машины, и др.) работают циклически. Любой замкнутый цикл состоит из процессов расширения и сжатия (см. рис. 4). На участках BC и CD газ расширяется и совершает положительную работу A1, которая равна площади фигуры под линией ABCDE. В процессах DF и FB газ сжимается и совершает отрицательную работу A2, величина которой равна площади под линией ABFDE. Таким образом, полная работа газа равна площади цикла. В прямом цикле A > 0; в обратном цикле A < 0.
|
рис.4 |
|||||||||||||||||||||
|
|
|||||||||||||||||||||
25.2 Один из основных законов электродинамики был открыт в 1826 г. немецким учителем физики Георгом Омом. Он установил, что сила тока в проводнике пропорциональна разности потенциалов
Рассмотрим
неоднородный участок цепи, участок,
содержащий источник ЭДС (т.е. участок,
где действуют неэлектрические
силы). Напряженность
Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке U12(рис. 7.4).
т.к.
Напряжение на концах участка цепи совпадает с разностью потенциалов только в случае, если на этом участке нет ЭДС, т.е. на однородном участке цепи. Запишем обобщенный закон Ома для участка цепи содержащей источник ЭДС:
Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных. В электротехнике часто используют термин падение напряжения – изменение напряжения вследствие переноса заряда через сопротивление
В
замкнутой цепи:
где
Тогда закон Ома для замкнутого участка цепи, содержащего источник ЭДС запишется в виде
ЭДС
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС
можно выразить через напряжённость
электрического поля
сторонних сил (
ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю. ЭДС индукции Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
где
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы электрического поля, совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.
При
этом считается, что перенос пробного
заряда не
изменяет
распределения зарядов на источниках
поля (по определению пробного
заряда).
В потенциальном электрическом поле
эта работа не зависит от пути, по
которому перемещается заряд. В этом
случае электрическое напряжение
Альтернативное
определение —
— интеграл
от проекции поля эффективной
напряжённости
поля
Единицей измерения напряжения в системе СИ является вольт
26 билет Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил. Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
- закон сохранения энергии для термодинамич. системы, согласно к-рому работа может совершаться только за счёт теплоты или к.-л. др. формы энергии. Поэтомуработу и кол-во теплоты можно измерять в одних единицах - Джоулях (1 Дж)П. н. т. сформулировано как закон природы Ю. <Р. Майером в 1842 и установлено экспериментально Дж. Джоулем в 1843. П. н. т. можно формулировать как невозможность существования вечного двигателя 1-го рода, к-рый совершал бы работу, не черпая энергию изк.-л. источника. Согласно П. н. т., теплота Q, сообщаемаясистеме, равна сумме приращения внутр. энергии . и работы, производимойсистемой против внеш. сил: Q = U2-U1 + A; прибесконечно малом изменении состояния системы: Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδQ, полученного телом, к соответствующему приращению его температуры δT: Единица измерения теплоёмкости в системе СИ — Дж/К.
Cp = Cv + R Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной В металлах! Металлы состоят из положительно заряженных ионов, находящихся в узлах кристаллической решетки и совокупности свободных электронов. Вне электрического поля свободные электроны движутся хаотически, подобно молекулам идеального газа, а потому рассматриваются в классической электронной теории как электронный газ. Под действием внешнего электрического поля меняется характер движения свободных электронов внутри металла. Электроны, продолжая хаотичные движения, вместе с тем смещаются в направлении действия сил электрического поля. Следовательно, электрический ток в металлах - это упорядоченное движение электронов. В газах! При нормальных условиях газы состоят из нейтральных молекул, а поэтому являются диэлектриками. Так как для получения электрического тока необходимо наличие заряженных частиц, то молекулы газа следует ионизировать (оторвать электроны от молекул). Для ионизации молекул необходимо затратить энергию - энергию ионизации, количество которой зависит от рода вещества. Так, энергия ионизации минимальна для атомов щелочных металлов, максимальна - для инертных газов. Ионизировать молекулы можно при нагревании газа, при облучении его различного рода лучами. Благодаря дополнительной энергии возрастает скорость движения молекул, нарастает интенсивность их теплового движения и при соударении отдельные молекулы теряют электроны, превращаясь в положительно заряженные ионы.
Электроны, оторвавшись от молекулы могут присоединятся к нейтральным молекулам, образуя при этом отрицательно заряженные ионы.
Следовательно, при ионизации появляются три типа носителей зарядов: положительные ионы, отрицательные ионы и электроны.
В вакууме! отсутствуют заряженные частиц, а следовательно, он является диэлектриком. Т.е. необходимо создать определенные условия, которые помогут получить заряженные частицы. Свободные электроны есть в металлах. При комнатной температуре они не могут покинуть металл, т. к. удерживаются в нем силами кулоновского притяжения со стороны положительных ионов. Для преодоления этих сил электрону необходимо затратить определенную энергию, которая называетсяработой выхода. Энергию, большую или равную работе выхода, электроны могут получить при разогреве металла до высоких температур.
При нагревании металла количество электронов с кинетической энергией, большей работы выхода, увеличивается, поэтому из металла вылетает большее количество электронов. Испускание электронов из металлов при его нагревании называют термоэлектронной эмиссией. Для осуществления термоэлектронной эмиссии в качестве оного из электродов используют тонкую проволочную нить из тугоплавкого металла (нить накала). Подключенная к источнику тока нить раскаляется и с ее поверхности вылетают электроны. Вылетевшие электроны попадают в электрическое поле между двумя электродами и начинают двигаться направленно, создавая электрический ток. Явление термоэлектронной эмиссии лежит в основе принципа действия электронных ламп: вакуумного диода, вакуумного триода.
27 билет
1)Изохорный
процесс (V=const).
Диаграмма этого процесса (изохора) в
координатах р, V изображается прямой,
параллельной оси ординат (рис. 1), где
процесс 1—2 есть изохорное нагревание,
а 1—3 — изохорное охлаждение. При
изохорном процессе газ не совершает
работы над внешними телами, т. е.
откуда
2) Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками. В Международной системе единиц (СИ) ёмкость измеряется в фарадах. В системе СГС в сантиметрах. Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводникибесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны Q, С,. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, затратив на это работу, равную
Чтобы зарядить тело от нулевого потенциала до , необходимо совершить работу
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
Билет 28
Адиабати́ческий,
или адиаба́тный
проце́сс (от др.-греч. ἀδιάβατος —
«непроходимый») — термодинамический
процесс в
макроскопической системе, при котором
система не обменивается тепловой
энергией с
окружающим пространством .
Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы[3]. Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике. Уравнение политропы НЕ ЗНАЮ
Напряженность
электростатического поля, согласно
(88.5), зависит от свойств среды: в
однородной изотропной среде
напряженность поля Е обратно
пропорциональна e.
Вектор напряженности Е,
переходя через границу диэлектриков,
претерпевает скачкообразное изменение,
создавая тем самым неудобства при
расчетах электростатических полей.
Поэтому оказалось необходимым помимо
вектора напряженности характеризовать
поле еще вектором
электрического смещения, который
для электрически изотропной среды,
по определению,
равен Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Аналогично, как и поле Е, поле D изображается с помощью линий электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь. Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность
где Dn — проекция вектора D на нормаль n к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике:
т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. Для вакуума Dn = e0En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность (ср. с (81.2)) равен
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (81.2) для поля Е в самом общем виде можно записать как
где
29 билет Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса). Энтропия в информатике — степень неполноты, неопределённости знаний. Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно. 2) Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией. Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков). Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема. Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает всегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры. Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.
Билет 30 2) Твердые диэлектрики - это чрезвычайно широкий класс веществ, содержащий вещества с радикально различающимися электрическими, теплофизическими, механическими свойствами. Например, диэлектрическая проницаемость меняется от значения, незначительно превышающего 1, до более чем 50000, в зависимости от типа диэлектриков: неполярный, полярный, сегнетоэлектрик. В главе 1 приводились определения различных типов диэлектриков. Вкратце коснемся этих определений применительно к твердым диэлектрикам. Неполярный диэлектрик - вещество, содержащее молекулы с преимущественно ковалентной связью. Полярный диэлектрик - вещество, содержащее дипольные молекулы или группы, или имеющее ионы в составе структуры. Сегнетоэлектрик - вещество, имеющее в составе области со спонтанной поляризацией. Механизмы поляризации у них резко различаются: - чисто электронная поляризация у неполярных диэлектриков типа полиэтилена, полистирола, при этом -мала, не более 3, диэлектрические потери тоже малы; - ионная поляризация у ионных кристаллов типа NaCl или дипольная у полярных диэлектриков типа льда, при этом может находиться в пределах от 3-4 до 100, диэлектрические потери могут быть весьма значительны, в особенности на частотах вращения диполей и других резонансных частотах; - доменная поляризация у сегнетоэлектриков - при этом максимальна и может достигать 10000-50000, диэлектрические потери могут быть весьма значительны, в особенности на резонансных частотах и в области повышенных частот. Особенности механизмов проводимости в твердых диэлектриках - концентрация носителей очень мала, подвижность ионов в гомогенных материалах очень мала, подвижность электронов в чистых материалах велика, в технически чистых - мала. Механизмы электропроводности различны в разных веществах. Ионная проводимость реализуется у полидисперсных диэлектриков (картон, бумага, гетинакс, дерево) и ионных кристаллов. В первом случае ионы передвигаются по границам раздела, образованным слипшимися дисперсными частицами. Появление носителей заряда сильно связано с влажностью этих материалов и определяется, как рассматривалось в лекциях 2 и 9 диссоциацией примесей и полярных групп основного вещества на поверхности раздела. В случае ионных кристаллов, в проводимости участвуют ионы основного вещества, примесей, дефекты структуры. Электронная проводимость реализуется у титанатов бария, стронция и т.д., электронная, дырочная и ионная проводимость у полимеров.
Билет 26. 1.Внутренняя энергия системы может изменяться в результате различных процессов: совершения над системой работы (при сжимании газа его температура повышается, следовательно, изменяется внутренняя энергия), сообщения системе количества теплоты (энергия передается системе в процессе теплообмена). При взаимодействии тел происходит переход энергии из одного вида в другой, а также обмен механической и внутренней энергией. При нагревании газа под поршнем энергия теплового движения молекул переходит в механическую энергию движения поршня. При соприкосновении тел передается их внутренняя энергия, энергия теплового движения молекул. При этих превращениях соблюдается закон сохранения и превращения энергии, получивший название первого начала термодинамики: ΔQ=ΔU+A (48) количество теплоты ΔQ, переданное системе, идет на изменение ее внутренней энергии ΔU и на совершение системой работы A. Количество теплоты ΔQ считается положительным, если тепло передается из окружающей среды данной системе, механическая работа A считается положительной, если система производит работу над окружающими телами. Первое начало термодинамики в дифференциальной форме: δQ=dU+δA, где δQ - бесконечно малое количество теплоты (не является полным дифференциалом), dU - бесконечно малое изменение внутренней энергии системы (полный дифференциал), δA - элементарная работа (не является полным дифференциалом). Согласно (48), единицы измерения количества теплоты в СИ: [Q]=Дж . Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: c=δQ/mdT (49) Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К: C=δQ/υdT (50) В системе СИ: [c]=Дж/кг·К, [C]=Дж/моль·К. Связь удельной и молярной теплоемкости: C=cM, (51) где M - молярная масса вещества.
Сообщение телу теплоты вызывает изменение его состояния и в общем случае сопровождается изменением температуры. Было замечено, что для нагрева до одной и той же температуры двух различных тел одинаковой массы и в одинаковых условиях требуется различное количество теплоты. Следовательно, существует какое-то свойство тела, определяющее изменение его температуры в процессе подвода или отвода теплоты. Это свойство называют теплоемкостью тела. Таким образом, теплоемкость тела – это величина, характеризующая способность тела изменять свою температуру с подводом или отводом теплоты. Она равна количеству теплоты, которое надо подвести к телу, чтобы изменить его температуру на 1 К:
Cp = Cv + R Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной....;)
2. § 102. Элементарная классическая теория электропроводности металлов Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости метал¬лов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследст¬вии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории. Первый из таких опытов — опыт Рикке* (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (?3,5?106 Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны. *К. Рикке (1845—1915) — немецкий физик. Для доказательства этого предположения необходимо было определить знак и ве¬личину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опы¬ты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881—1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных метал¬лов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны. |
|
Билет 28.
1
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Адиабатический
процесс - это такое изменение состояний
газа, при котором он не отдает и не
поглощает извне теплоты. Следовательно,
адиабатический процесс характеризуется
отсутствием теплообмена газа с окружающей
средой. Адиабатическими можно считать
быстро протекающие процессы. Так как
передачи теплоты при адиабатическом
процессе не происходит, то ![]() и
уравнение I начала термодинамики
принимает вид
и
уравнение I начала термодинамики
принимает вид
|
(9.20) |
Уравнение политропы удобно использовать для описания действительных процессов, происходящих в тепловых машинах, в частности в двигателях внутреннего сгорания (поршневых и газотурбинных), в компрессорах (поршневых и центробежных). Напишем уравнение политропы (1.88) в виде pll"v = const.
2



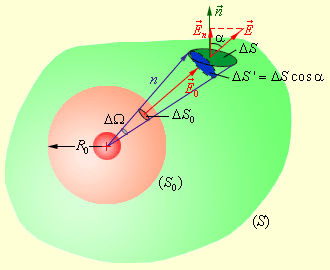




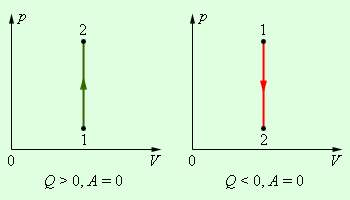



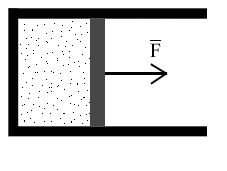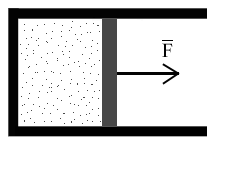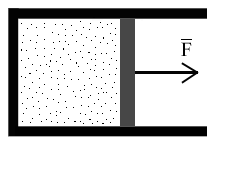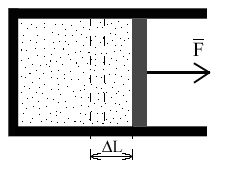
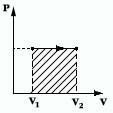
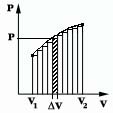
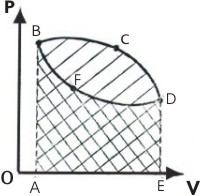
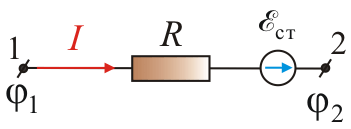 Рис.
7.4
Рис.
7.4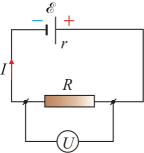 Рис.
7.5
Рис.
7.5
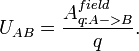

 Вакуумный
диод
Вакуумный триод
Вакуумный
диод
Вакуумный триод