2.Закон Ома для участка цепи в дифференциальной форме. Удельные сопротивление, проводимость. Плотность тока.

Если в закон Ома подставить ρ вместо R, получим ,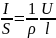

где величина, обратная удельному сопротивлению (ρ) ϒ = 1/ ρ, называется удельной электрической проводимостью вещества проводника. [См/м] См – сименс.

Учитывая, что U/l = E – напряженность поля в проводнике, I/S = j - плотность тока, формулу можно записать в виде j = ϒE

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадут.

j = ϒE – закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Плотность тока j – это векторная физическая величина, показывающая направление электрического тока.

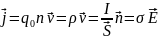
Билет 21

1. Явление диффузии в термодинамически неравновесных системах

В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориентирована в направлении переноса.

Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фука:

jm=-D*dr/dx

где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dr/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dr/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов,D=1/3*<v>8<L>

2.Плоский воздушный конденсатор. Энергия конденсатора.

КОНДЕНСАТОР электрический (от лат. сondensator, — тот, кто уплотняет, сгущает), устройство, предназначенное для получения нужных величин электрической емкости и способное накапливать (перераспределять) электрические заряды.

Плоский конденсатор представляет собой две плоские пластины, расстояние между которыми d мало по сравнению с их линейными размерами. Это позволяет пренебречь малыми областями неоднородности электрического поля у краев пластин и считать, что все поле однородно и сосредоточено между пластинами. Заряд конденсатора Q — это заряд положительно заряженной пластины.

Емкость плоского конденсатора С:

С= ξξо S/d

S — площадь каждой обкладки или меньшей из них, d — расстояние между обкладками, eо— электрическая постоянная, e — относительная диэлектрическая проницаемость вещества, находящегося между обкладками. Заполнение пространства между пластинами диэлектриком увеличивает емкость в e раз.

Энергия, запасенная заряженным до постоянного напряжения U плоским электрическим конденсатором, равна:

W = CU2/2.

При заряде конденсатора внешний источник расходует энергию на разделение зарядов на положительные и отрицательные. Которые будут находиться на обкладках конденсатора. Следовательно, исходя из закона сохранения энергии, она никуда не пропадает, а остается в конденсаторе. Энергия в конденсаторе запасается в виде силы взаимодействия положительных и отрицательных зарядов находящихся на его обкладках. То есть в виде электрического поля. Которое сосредоточено между пластинами. Это взаимодействие стремится притянуть одну обкладку к другой, поскольку, как известно разноименные заряды притягиваются.

Как известно из механики F=mg, аналогично в электрике F=qE, роль массы играет заряд, а роль сили притяжения напряжённость поля.

Работа по перемещению заряда в электрическом поле выглядит так:A=qEd1-qEd2=qEd

C другой же стороны работа также равна разнице потенциальных энергий A=W1-W2=W.

Таким образом используя эти два выражения можно сделать вывод что потенциальная энергия накопленная в конденсаторе равна:

W=qEd

Формула 1 — Энергия заряженного конденсатора

Не трудно заметить, что формула очень похожа на потенциальную энергию из механики W=mgh.

Если провести аналогию с механикой: Представим камень, находящийся на крыше здания. Здесь взаимодействует масса земли с массой камня посредством силы тяжести, а здание высотой h противодействует силе гравитации. Если здание убрать камень упадет, следовательно, потенциальная энергия перейдет в кинетическую.

В электростатике же есть два разноименных заряда стремящихся притянутся друг к другу им противодействует диэлектрик толщиной d находящийся между обкладками . Если обкладки замкнуть между собой то потенциальная энергия заряда перейдет в кинетическую то есть в тепло.

В электротехнике формула для энергии в таком виде не применяется. Ее удобно выразить через емкость конденсатора и напряжение, до которого он заряжен.

Так как заряд конденсатора определяется зарядом одной из его пластин то напряжённость поля, создаваемая ею, будет равна E/2. Поскольку общее поле складывается из полей создаваемых обеими обкладками заряжении одинаково, но с противоположным знаком.

Следовательно, энергия конденсатора будет иметь вид: W=q(E/2)d

Поскольку напряжение можно выразить через напряжённость и расстояние(U=Ed) подставим его в нашу формулу получим: W=qU/2

А теперь используя выражение для емкости, C=q/U получим окончательный результат.

Энергия заряженного конденсатора имеет вид:

Wэл=CU^2/2

Формула 2 — Энергия заряженного конденсатора

Билет 22.

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

Перенос энергии в форме теплоты подчиняется закону Фурье:

Je=-лямда*dT/dx

где jE — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, l — теплопроводность, dT/dx — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и – противоположны). Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.

Можно показать, что

лямда=1/3cvp<v><l>

(48.2)

где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), r — плотность газа, <v> — средняя скорость теплового движения молекул, <l> — средняя длина сво­бодного пробега.

Основные понятия и законы электростатики

Электростатика — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов.

Между одноимённо заряженными телами возникает электростатическое (или кулоновское) отталкивание, а между разноимённо заряженными — электростатическое притяжение. Явление отталкивания одноименных зарядов лежит в основе создания электроскопа — прибора для обнаружения электрических зарядов.

^ Закон Кулона: сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:

Коэффициент пропорциональности k в этом законе равен:

В СИ коэффициент k записывается в виде

где ?0 = 8,85·10?12 Ф/м (электрическая постоянная).

^

Напряженность электрического поля

Точечными зарядами называют такие заряды, расстояния между которыми гораздо больше их размеров.

Электрические заряды взаимодействуют между собой с помощью электрического поля. Для качественного описания электрического поля используется силовая характеристика, которая называется напряженностью электрического поля Напряженность электрического поля равна отношению силы, действующей на пробный заряд, помещенный в некоторую точку поля, к величине этого заряда:

E=F/q0

Направление вектора напряженности совпадает с направлением силы, действующей на положительный пробный заряд. [E] = B/м. Из закона Кулона и определения напряженности поля следует, что напряженность поля точечного заряда равна

E=k*q/r^2

где q — заряд, создающий поле; r — расстояние от точки, где находится заряд, до точки, где создается поле. Если электрическое поле создается не одним, а несколькими зарядами, то для нахождения напряженности результирующего поля используется принцип суперпозиции электрических полей: напряженность результирующего поля равна векторной сумме напряженностей полей, созданных каждым из зарядов—источников в отдельности:

E=E1+E2+...+En

^

Работа электрического поля

Работа электрического поля при перемещении заряда:

найдем работу перемещения положительного заряда силами Кулона в однородном электрическом поле. Пусть поле перемещает заряд q из точки 1 в точку 2:

A=qE(d1-d2)=-(qEd2-qEd1)

В электрическом поле работа не зависит от формы траектории, по которой перемещается заряд. Из механики известно, что если работа не зависит от формы траектории, то она равна изменению потенциальной энергии с противоположным знаком:

A=-(Wp2-Wp1)

Отсюда следует, что:

Wp=qEd

Билет 23

1

В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориентирована в направлении переноса.

Внутреннее трение (вязкость). Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

(48.5)

F=h*|dv/dx|*S

где h — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно представить в виде

jp=-h*dv/dx

(48.6)

где jp — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, dv/dx — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и противоположны).

Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

h=1/3*p<v><l>

(48.7)

Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математических выражений обусловлено общностью лежащего в основе явлений теплопровод­ности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.

Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетического смысла коэффициентов l, D и h. Выражения для коэффициентов переноса выводятся из кинетической теории. Они записаны без вывода, так как строгое рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (48.2), (48.4) и (48.7) связывают коэффициенты переноса и характеристики теплового движения молекул. Из этих формул вытекают простые зависимости между l, D и h:

h=pD

лямда/(hcv)=1

2.

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

dNe=EdS_=EdScosальфа

где альфа - угол между силовой линией и нормалью n к площадке dS; dS_ - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

Ne=интеграл по S*EdScosальфа (13.4)

Так как Ecosальфа=En , то

Ne=интеграл по S*EndS (13.5)

где En - проекция вектора E на нормаль и к поверхности dS.