Билет №1

Система отсчёта в механике, совокупность системы координат и часов, связанных с телом, по отношению к которому изучается движение (или равновесие) каких-нибудь других материальных точек или тел. Любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел.

1.1.1 Кинематика поступательного движения

При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.

Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.

Линию, по которой движется материальная точка в пространстве, называют траекторией.

Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r₀, направленный от положения точки в начальный момент времени к ее положению в конечный момент.

Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета. 

2) Два одноименных заряда, будь то два протона либо два электрона сопротивляются сближению и пытаются удалиться друг от друга. Этот процесс обычно называют отталкиванием. Первый закон описывающийвзаимодействие электрических зарядов говорит: заряды с одинаковым знаком (т. е. одноименные) отталкиваются друг от друга (рис.2.1.). Второй закон взаимодействия электрических зарядов гласит: разноименные (заряды с разным знаком) притягиваются друг к другу.

  Отрицательно заряженные электроны притягиваются к положительно заряженным протонам в ядре атома. Почему же электрон остается на орбите и не падает на ядро? Это происходит в результате того, что сила притяжения электрона уравновешивается центростремительной силой, возникающей за счет вращения электрона вокруг ядра.  Значение величины сил отталкивания и притяжения, существующих между двумя заряженными телами, зависит от следующих факторов: расстояния между телами и их зарядов.  Заряд отдельного электрона очень мал, поэтому в практике не используется. Принятой в мире единицей измерения заряда является кулон (Кл). Она названа в честь французского ученого Шарля Кулона, обозначается буквой Q. Один  кулон это 6,28*10¹⁸ зарядов электронов. Электрические заряды возникают за счет смещения электронов. Когда имеется дефицит электронов в одной точке и избыток  в другой, как мы уже говорили, возникает разность потенциалов. Если две точки, между которыми существует разность потенциалов, соединить проводником, то по проводнику потекут электроны. Тогда этот поток электронов называется электрическим током.

Закон Кулона - это закон взаимодействия двух неподвижных точечных зарядов. Закон Кулона формулируется следующим образом: Сила электрического взаимодействия между двумя точечными зарядами в вакууме пропорциональна этим зарядам и обратно пропорциональна квадрату расстояния между ними.

При взаимодействии одноименные заряды отталкиваются, разноименные притягиваются. Силы Кулона направлены по прямой, соединяющей заряды.

Закон Кулона для взаимодействия точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга, записывается формулой:

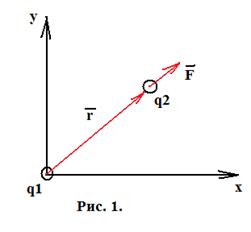
Сила отталкивания F, действующая на заряд Q2 со стороны одноименного заряда Q1, совпадает по направлению с радиусом-вектором r, проведенным из Q1 к этому заряду.

Билет№2

1)кинематика вращательного движения: При описании вращательного движения твердого тела относительно неподвижной в данной системе отсчета принято использовать векторные величины особого рода. В отличие от рассмотренных выше полярных векторов r (радиус-вектор), v (скорость), a (ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными (лат. axis – ось).

Элементарный поворот dφ – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта.

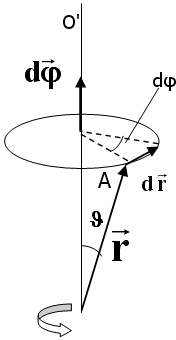  Рис.1.4. К определению направления аксиального вектора

Линейное перемещение dr произвольной точки А твердого тела связано с радиусом-вектором r и поворотом dφ соотношением dr=rsinα•dφ или в векторном виде через векторное произведение:

dr=[dφ,r] (1.9)

Соотношение (1.9) справедливо именно для бесконечно малого поворота dφ.

Угловая скорость ω – аксиальный вектор, определяемый производной вектора поворота по времени:

ω=dφ/dt=φ'

Вектор ω, как и вектор dφ, направлен вдоль оси вращения по правилу правого винта (рис.1.5).

 

Р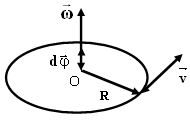 ис.1.5. К определению направления вектора

Угловое ускорение β – аксиальный вектор, определяемый производной вектора угловой скорости по времени:

β=dω/dt=d²φ/dt²=ω'=φ''

При ускоренном движении вектор β по направлению совпадает с ω (рис. 1.6,а), а при замедленном - векторы β и ω направлены противоположно друг другу (рис. 1.6,б).

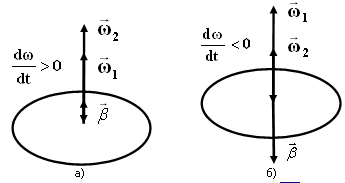  Рис.1.6. Связь между направлениями векторов ω и β

Важное замечание: решение всех задач на вращение твердого тела вокруг неподвижной оси по форме аналогично задачам на прямолинейное движение точки. Достаточно заменить линейные величины x, v_x, a_x на соответствующие им угловые φ, ω и β, и мы получим уравнения, аналогичные (1.6) -(1.8).

2) Напряженность электростатического поля - это силовая характеристикаэлектростатического поля, численно равная силе, действующей на единичный положительный заряд.

Напряженность электростатического поля - векторная величина.

Напряженность электрического поля:

E = F/Qпробный

Напряженность электростатического поля (точечного заряда):

 

где r - расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность.

Единица напряженности - вольт на метр (В/м)

Электростатическое поле представляется графически силовыми линиямиили линиями напряженности .

Принцип суперпозиции электрических полей: Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.

(13.3)

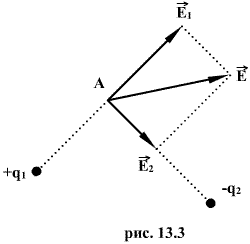
Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке А поля двух точечных зарядов   и   (рис. 13.1). Сложение векторов   и   производится по правилу параллелограмма. Направление результирующего вектора   находится построением, а его абсолютная величина может быть подсчитана по формуле

Билет№3