29. Доверительный интервал для математического ожидания при известной дисперсии.

П усть

Известно

Т ребуется найти доверит. интервал для a с надежностью .

Т очечная оценка для мат. ожидания:

Н айдем точность .

П усть — выборка, полученная в результате наблюдения за X.

З начения меняются от выборки к выборке.

П оэтому, можно считать, что

К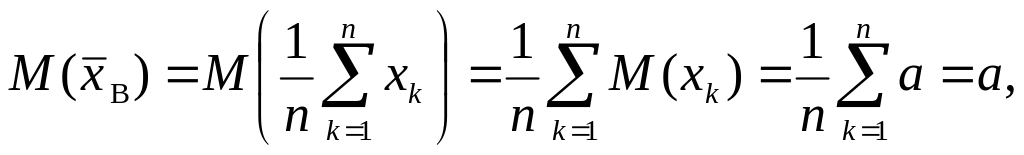 роме того, выборочное среднее также является СВ, распределенная нормально, причем

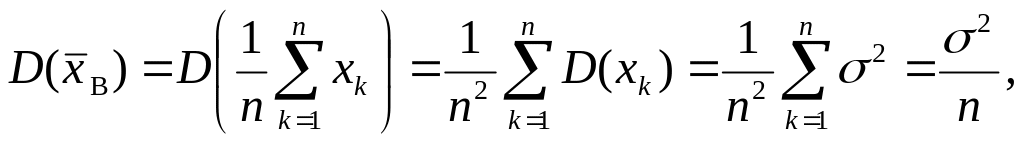
Т ак как то

О бозначим Тогда

п ричем

Поэтому

т .е. с надежностью можно утверждать, что доверительный интервал

п окрывает неизвестный параметр a, причем точность оценки равна

30.Доверительный интервал для математического ожидания при неизвестной дисперсии.

П усть

И звестно

Т ребуется найти доверит. интервал для a с надежностью .

Т очечная оценка для мат. Ожидания :

Найдем точность .

П усть S — исправленное среднее квадратическое отклонение.

Рассмотрим СВ

М ожно показать, что СВ T имеет распределение Стьюдента с степенями свободы.

Н айдем так, чтобы

Р азделим обе части неравенства в скобках на

Обозначим Тогда

В еличину определяют по таблице распределения Стьюдента.

Поэтому

т .е. с надежностью можно утверждать, что доверительный интервал

п окрывает неизвестный параметр a, причем точность оценки равна

31. Понятие о проверке статистических гипотез. Нулевая и альтернативная гипотезы. Ошибки первого и второго рода.

Статист. гипотезой назыв. гипотеза о виде неизвестного распределения или о параметрах известного распределения. Нулевой (основной) называется выдвинутая гипотеза . Конкурирующей (альтернативной) назыв. гипотеза H₁, кот. противоречит нулевой. Статистическим критерием назыв. случайная величина, которая служит для проверки гипотезы .

Ошибка первого рода возникает, когда мы отвергаем прав. нул. гипотезу. Вероятность совершить ошибку первого рода называется уровнем значимости и обозн. : .

Ошибка второго рода возникает, когда мы отвергаем прав. гипотезу _. Вер-сть совершить ошибку второго рода обозн. : .Величину ошибки первого и второго рода исследователь выбирает самостоятельно: 0,01; 0,05; 0,001.Невозможно одновременно уменьшать ошибки первого и второго рода, так как речь идет об одних и тех же гипотезах.