Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

шпоры_вышка_все.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

3.27 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

№1.Случ. и их классификация. Операции над событиями.

Случ. событием явл исход некот. опыта (обознач.: А,В,С)

Элементар. события – непосредственные исходы некоторого опыта. (обозн. w₁,w₂,w_n)

Мн-во всех элем.х событий Ω - простр-во элем. событий.

Пример: опыт – подбрасывание игральной кости

Элементарные события: w₁ – выпало 1 очко, w₂ – вып. 2 очка..

Пространство эл. событий - Ω={w₁,w₂,w₃,w₄,w₅,w₆}

Случ. событие – А - выпало чётное кол-во очков А={2,4,6}

Случайное событие достоверное, если оно заведомо произойдёт. Обозначается: Ω

Случ. событие невозможное, если оно не произойдёт. Обозначается: Ǿ

Два случайных события называются несовместными, если проявление одного из них исключает появление другого в одном и том же опыте.

Пример: опыт – подбрасыв 2 кубика

Несовместные – А-сумма выпавших 5, В – оба чётные.

События А₁,А₂,А₃,… A_n образуют полную группу, если:

1)они попарно несовместимы

2)в резул. опыта заведомо произ. только 1 из этих событий.

Пример: подбрасывают 1 кость. А₁ – выпадает менее 3-х очков, А₂ – от 3х до 4х, А₃ – более 4х.

Пусть А₁, А₂, А₃ – полная группа. Операции

- Сумма А и В назыв событие, состоящее в наступлении хотя бы одного из этих событий С=А+В.

- Произведение А и В – событие, состоящее в наступлении обоих событий одновременно С=А*В.

- Разность А и В – событие, сост. в том, что событие А происходит, а В – нет.

- Отрицание события А ( ) событие состоящее в том, что А не происходит.

Е сли и , то события A и B называются равными.

Геометрическая интерпретация(диаграммы Эйлера-Венна)

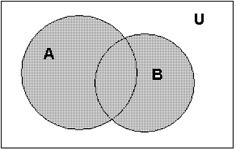
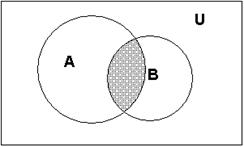
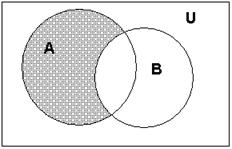
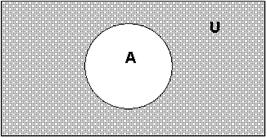
А+В А*В А-В

№2.Класич и статистич определения вероятности. Геометрические вероятности.

Классическое определение вероятности. Пусть приизводится классический опыт, где возможно n исходов и эти исходы можно представить в виде полной группы несовместных равновозможных событий. Случай w, который приводит к наступлению события А – благоприятный для этого события.

К лассической вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, у общему числу случаев, те

Пример: подбрасыв 2 кости, найти вер-сть выпадения 10.

О бщ число исходов n=36, m = 3 – благоприятные исходы. Ответ:

Св-ва классич вероятности:

Вероятность в след рамках 0Р(А)1
Вероятность невозможного события равно нулю Р(Ǿ)=0
Вероятность достоверного события равна 1 Р(Ώ)=1
В 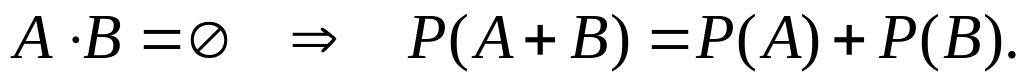ероятность суммы несовместных событий равна сумме вероятностей этих событий
Е 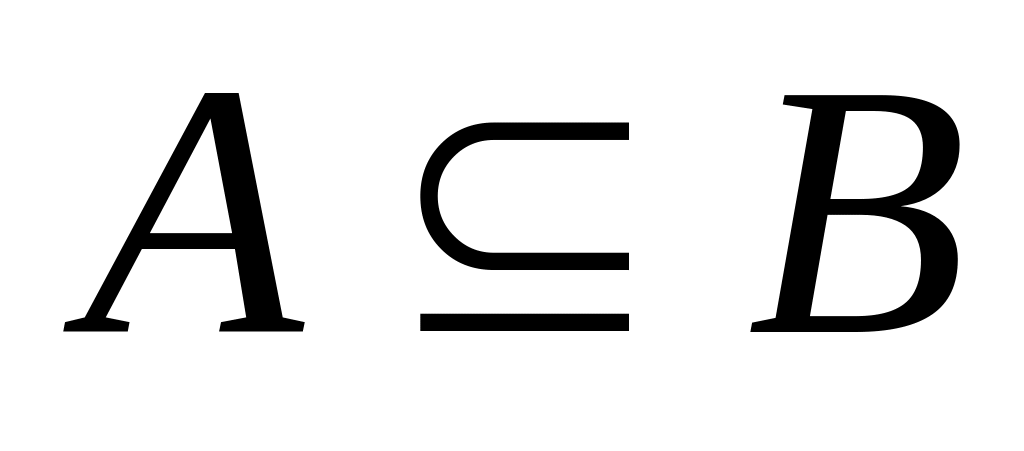сли , то Р(А)≤Р(В)

Статистическое определение вер-ти. Пусть проводится опыт в кот. наблюдается событие А, где возможно конечное число исходов и они не равновозможны, n_A– число появлений события А (частота события А), n – число всех опытов.

- относительная частота события А.

Свойства относительной частоты такие же как св-ва классической вероятности.

Свойство статической устойчивости: с увеличением числа опытов относительная частота принимает значения, близкие к некоторому постоянному числу.

Статической вероятностью события А называется число, около которого колеблется относительная частота события А при достаточно большом числе испытаний.

Г еометрическое определение вероятности. Пусть проводится опыт, когда возможно бесконечное кол-во исходов и эти исходы равновозможны. Рассмотрим на пл-ти обл G и обл g такую, что

В обл G наудачу бросается точка Пусть А – точка попадёт в область g.

Г еометрической вероятностью события А называется отношение плащади области g к площади области G, те

Св-ва геометрич вероятности повторяют св-ва классической вероятности.+ геометрическое определение вероятности применимо и в случаях с линиями и обьёмными фигурами

№3.Формула сложения вероятностей. Условна вероятность. Формула умножения.

Пусть А, В – произвольные события. Тогда Р(А+В)= Р(А)+Р(В)-Р(АВ)

О чевидно, А+В=(А-В)+В. При этом (А-В)*В=Ǿ. По свойству 4 вероятности (вероятность суммы несовместных событий равна сумме вероятностей этих событий) Р(А+В)= Р(А-В)+Р(В).

Если А=(А-В)+АВ, (А-В)(АВ)=Ǿ, тогда Р(А)=Р(А-В)+Р(АВ).

Условная вероятность. Пусть А,В – произвольные события в некотором опыте. Условной вероятностью события В при условии, что событие А произошло называется величина Р(В/А)=Р(АВ)/Р(А), Р(А/В)=Р(АВ)/Р(В)

Формула умножения.

Р (АВ)= Р(А)*Р(В/А)=Р(В)*Р(А/В)

Р(А₁А₂…А_n)

Вероятность произведения двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло.

Пример 1: В экзаменационных материалах содержится 30 вопросов. Каждый билет содержит 3 вопроса. Студент знает 20. Найти вероятность того, что студент ответит:

на 3 вопроса; 2)на 2 вопроса; 3)хотя бы на один вопрос.

Решение:

А={студент ответил на 3 вопр}, А₁={студент ответил на первый вопрос}

А₂={студент ответил на второй вопр} А₃={студент ответил на третий вопрос}

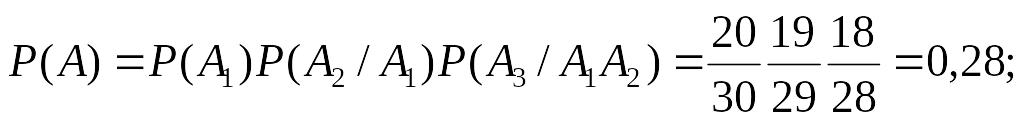
2) B = {студент ответил на 2 вопроса}

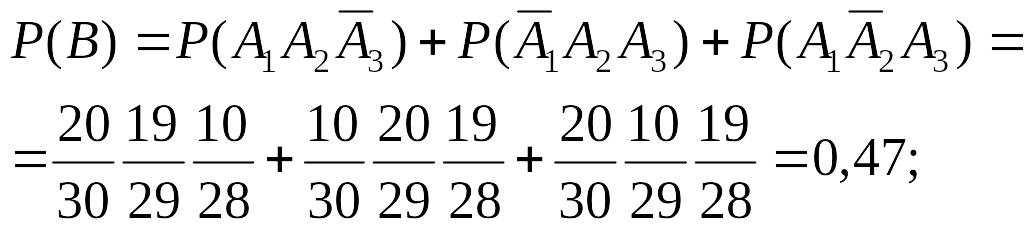
3) С = {студент ответил хотя бы на 1 вопрос}

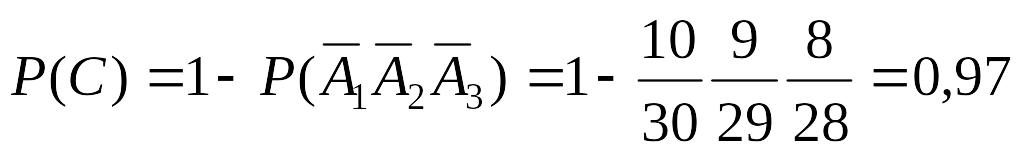№4.Формула полной вероятности. Формула Байеса.

Ф ормула полной вероятности. Пусть события Н₁, Н₂….Н_n образуют полную группу. Тогда для любого события А справедлива формула Док-во:

Формула Байеса. Пусть события Н₁, Н₂….Н_n образуют полную группу. Тогда для любого события А справедлива формула

№5.Схема независимых испытаний Бернулли.

№6.Теорема Пуассона. Лок. пред. теорема Муавра–Лапласа. Интегр. предельная теорема Муавра–Лапласа.

П уассона. Пусть в схеме Бернулли число испытаний n неограниченно возрастает, Вероятность р неограниченно уменьшается , произведение a=np явл. постоянной величиной. Тогда для любого фиксированного m справедлива формула:

Лок теорема. Пусть в схеме Бернулли число испытаний n неограниченно возрастает Вероятность постоянна. Тогда :

Где

функция Гаусса.

Значения функции находят по специальной таблице, при этом учитывая, что

Интегральная . Пусть в схеме Бернулли число испытаний n неограниченно возрастает , вероятность постоянна. Тогда

№7.Случайная величина и закон ее распределения.

Случайной величиной называют величину, которая принимает в результате опыта случайное значение. ( дискретные, непрерывные, сингулярные)

Дискретной называется случайная величина, которая принимает конечное или счетное множество значений.

Действия над дискретными СВ:

Даны две дискр. СВ : X: x1+x2+…+Xn; и Y: y1+y2…+yn

1 . Сложение, вычитание, умножение:

2 . Умножение на число: Z=cX,

Значение СВ Z:

Дискретные СВ X и Y наз. независимыми, если

Непрерывной называется случайная величина, значения которой принимает несчетное множество значений (значения заполняют целиком некоторые промежутки).

Правило, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения СВ.

Ряд распределения. Пусть Х –дискр СВ, приним. Значения х1,х2..,хn. р1=Р(Х=х1) – вер-сть, с кот СВ Х принимает значение х1, р2=Р(Х=х2) и т.д.

Х	х1	х2	…	хn	…
Р	p 1	p2	…	pn	…

Так как события образуют полную группу, то

Многоугольником (полигоном) распределения называют ломаную, соединяющую точки

№8. Функция распределения и ее свойства.

В ероятность того, что СВ примет значение, меньшее, чем x, называется функцией распределения вероятностей СВ X. Св-ва ф-ии:

1) Ф-я распределения ограничена.

2) F(x) — неубывающая функция:

3) Док-во:

4) Вероятность попадания СВ в зад. интервал равна приращению ф-ии распред. на этом интервале:

5) F(x) непрерывна слева:

Замечание. Ф-я распределения непрерывной СВ является непрерывной.

З амечание. Вероятность принятия непрерывной СВ фиксированного значения равна нулю.

Замечание. Для дискретной СВ:

Пример. Ряд распределения:

Х	1	2	3	4	5	6
Р	1/6	1/6	1/6	1/6	1/6	1/6

F(x)

5/6

2/3

1/2

1/3

1/6

1 2 3 4 5 6 х

№9.Плотность распределения.

П лотностью распределения вероятностей непрерывной СВ X называется производная ее функции распределения

По определению производной :

П лотностью распределения есть предел отношения вероятности попадания СВ X в промежуток к длине этого промежутка.

Замечание. По опред. можно записать:

Свойства:

1 ) Док-во:

П о св-ву 2 F(x) – неубыв. ф-я, значит т.е.

Д ок-во: Так как F(x) — первообразная для , то по формуле Ньютона-Лейбница

3) Cвойство нормировки.

Д ок-во:

Пример. Пусть Найти a. Решение по св-ву нормировки:

№10.Математическое ожидание.

М атем. ожиданием дискретной СВ называется сумма произведений ее значений на вероятности этих значений:

М ат. ожиданием непрерывной СВ с плотностью распределения наз. величина:

Математическое ожидание характеризует среднее значение случайной величины, взвешенное по вероятности.

Свойства мат. Ожидания:

1 ) Мат. ожидание постоянной равно этой пост.:

Д ок-во: Рассмотрим СВ X:

2 ) Док-во: По определению операции умножения на число:

Т огда

4) Док-во: с помощью свойств 1,2,3 :

5) Если СВ Х и У независимы, то

Док-во. В силу независимости

Тогда

№11.Дисперсия и среднеквадратическое отклонение.

Дисперсией СВ называется мат. ожидание квадрата отклонения СВ от своего математич. ожидания:

Для дискретной СВ:

Для непрерывной СВ:

Свойства дисперсии:

1) Дисперсия постоянной равна 0: Dc=0. Док-во:

2 ) Док-во:

3 ) Если СВ Х и У независимы, то

4 ) Док-во:

Средним квадратическим отклонением СВ называется квадратный корень из дисперсии, т.е. :

Свойства:

1 )

3 )

№12. Биномиальное распределение

Опыт (схема Бернулли): проводится n независимых испытаний, в каждом из которых возможно лишь 2 исхода: либо некоторое событие A наступит (с вероятностью p), либо событие A не наступит (с вероятностью q = 1 - p).

Случайная величина: X — количество появлений события A.

Значения случайной величины X:

Вероятности принятия этих значений:P(X=m)=C_n^m * p^m*qⁿ^-^m.(1)

Закон распределения, определяемый по формуле (1) называется биномиальным.

Ряд распределения:

X	0	1	2	…	m	…	n
P	qⁿ	C_n¹p q^n-1	C_n²p² q^n-2	….	C_n^mp^m q^n-m	…	pⁿ

Биномиальное распределение определяются двумя параметрами: n и p.

Определим их вероятностный смысл.

Н айдем числовые характеристики биномиального распределения.

СВ X представим в виде суммы незав. СВ:

где X_i — число появлений события A в i-м испытании.

X_i	0	1
P	q	p

Ряд распределения СВ:

Мат. ожидание СВ :

MX_i = 0*q+1*p=p

Дисперсия СВ : MX_i²=0²*q+1²*p=p

DX_i= MX_i²– (MX_i)²=p-p²=p(1-p)=pq.

Мат. ожидание СВ X (свойство 3): MX=MX₁+MX₂+…+MX_n=np.

Д исперсия СВ X (свойство 3): DX=DX₁+DX₂+…+DX_n=npq.

Среднее квадратическое отклонение СВ X:

№13. Распределение Пуассона

С В X имеет распределение Пуассона, если значения СВ X:

вероятности принятия этих значений:

где a — некоторый параметр.

Примеры: число вызовов на телефонную станцию; число опечаток в большом тексте; число бракованных изделий в большой партии.

Найдем числовые характеристики распределения Пуассона.

М атематическое ожидание.

Имеет место равенство:

Т огда

Дисперсия.

Рассмотрим равенство:

П родифференцируем по a:

Т огда

Замечание. Тот факт, что MX=DX является признаком распределения Пуассона.

№14. Геометрическое распределение

П усть проводится последовательность независимых испытаний, в каждом из которых возможно лишь 2 исхода: либо некоторое событие A наступит (с вероятностью p), либо событие A не наступит (с вероятностью

С лучайная величина: X — число испытаний до появления события A.

З начения случайной величины X:

вероятности принятия этих значений: (2)

Закон распределения, определяемый по формуле (2) называется геометрическим.

Н айдем числовые характеристики распределения Пуассона.

Математическое ожидание.

Р ассмотрим равенство:

Продифференцируем по q: (3)

Т огда

Дисперсия.

У множим обе части равенства (3) на q и продифференцируем по q:

Т огда

Среднее квадратическое отклонение СВ X:

№15. Равномерное распределение.

Н епрерывная СВ X имеет равномерное распределение на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке, а вне его равна нулю:

Обозначение:

Пример. Время ожидания транспорта; ошибка округления числа.

Н айдем параметр c. Используем условие нормировки:

З начит,

т.е.

График f(x):

Ф ункция распределения:

Е сли

Значит,

График

М ат. ожидание:

Д исперсия:

С реднее квадратическое отклонение:

№16.Показательное распределение.

Н епрерывная СВ X имеет показательное распределение, если ее плотность вероятности имеет вид:

— параметр распределения.

Пример. Время работы прибора до первого отказа; длительность времени обслуживания в системе массового обслуживания.

График f(x):

Ф ункция распределения.

Е сли

З начит,

График

Мат. ожидание:

Д исперсия.

С реднее квадратическое отклонение:

З амечание.

Тот факт, что является признаком показательного распределения.

№17. Нормальное распределение.

Н епрерывная СВ X имеет нормальное распределение, если ее плотность вероятности имеет вид:

— параметры распределения.

Обозначение:

П ример. Ошибка измерений; колебания курса акций, ошибки стрельбы.

Ф ункция распределения:

Е сли то нормальное распределение называется стандартным.

П ри этом

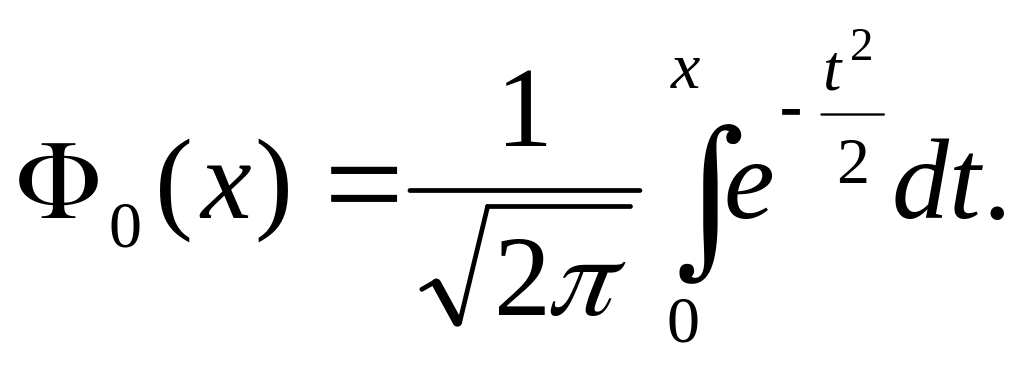
Н ормированная функция Лапласа:

Связь:

График f(x):

М ат. ожидание:

т 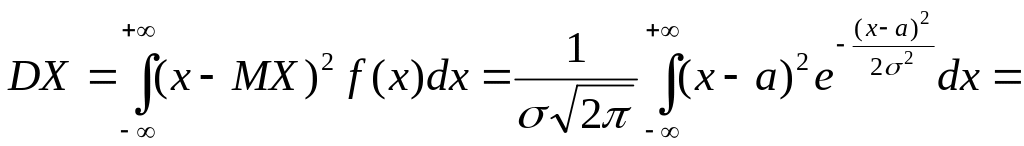.е.

Дисперсия:

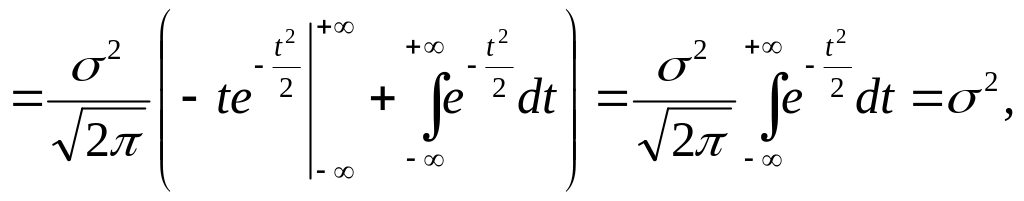
т.е. Ср. квадр. отклонение:

В ероятность попадания норм. СВ в заданный интервал:

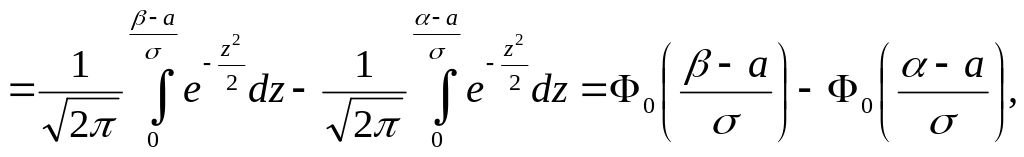
В ероятность отклонения нормальной СВ от своего мат. ожидания не более, чем на

Пусть Тогда

П равило «трех сигм»: практически в 100% случаев значения нормальной СВ заключены в интервале

№18.Многомерные СВ.

П ример. Производится выстрел по мишени. Для того, чтобы определить точку попадания, необходимы две величины: абсцисса и ордината.

У порядоченный набор случ. величин

называют n-мерной случайной величиной (системой n случайных величин).

О дномерные СВ называются компонентами n-мерной случайной величины

n-мерная случайная величина называется дискретной (непрерывной), если все ее компоненты дискретные (непрерывные) СВ. n-мерная случайная величина называется смешанной, если ее компоненты — СВ разных типов.

Б удем рассматривать двумерные СВ. Упорядоч. пара двух СВ называется двумерной случайной величиной.

Законы распределения СВ: с помощью таблицы, функция распределения, плотность распределения.

З аконы распределения дискретной СВ (X,Y) можно задать формулой или с помощью таблицы

X\Y	y₁	y₂	…	y_m
x₁	p₁₁	p₁₂	…	p_1m
x₂	p₂₁	p₂₁	…	p_2m
…	…	…	…	…
x_n	p_n1	p_n2	…	p_nm

З амечание.

З амечание. Зная закон распределения двумерной СВ можно найти законы распределения ее компонент:

П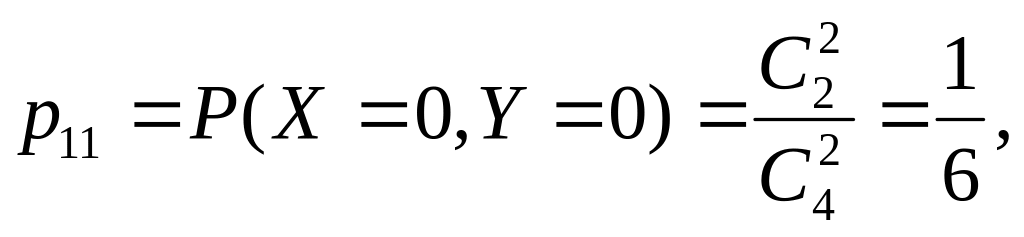 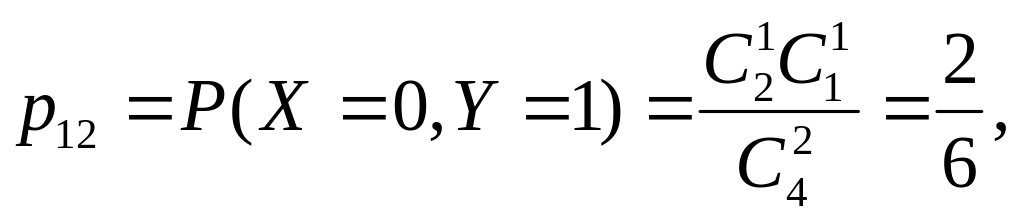ример. В урне 4 шара: 2 бел., 1 чер., 1 син.. Наудачу извл. 2 шара. Пусть СВ X — число чер. шаров среди выбр., СВ Y — син.. Сост-ть закон распр. двумер. СВ (X,Y). Найти законы распределения X и Y. Решение. Значения СВ X : 0,1. Значения СВ Y : 0,1.

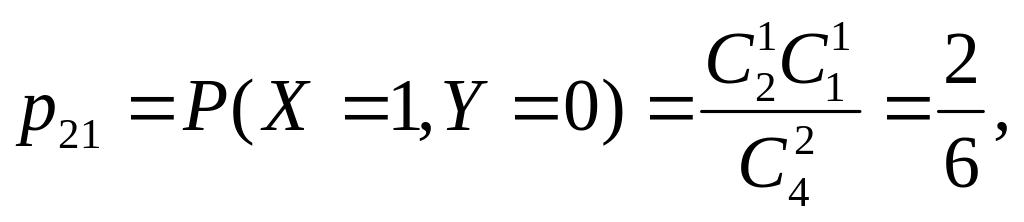
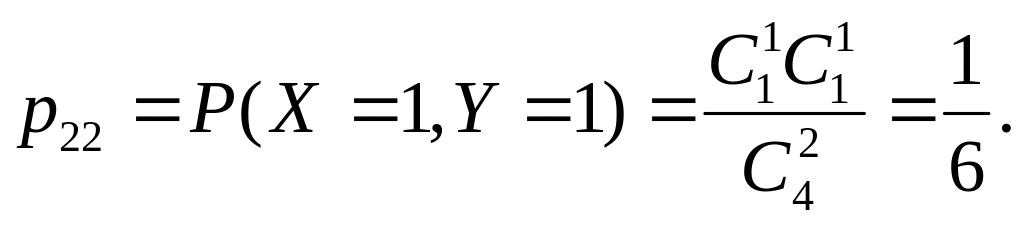
X \ Y	0	1
0	1/6	2/6
1	2/6	1/6

Таблица распределения:

К онтроль:

З акон распред. СВ X.

X	0	1
P	1/2	1/2

Y	0	1
P	1/2	1/2

акон распределения СВ Y.

№19. Совместная функция распределения СВ.

Ф ункцией распределения двумерной СВ (X,Y) называется функция

(X,Y)

(x,y)

Для дискретной двумерной СВ (X,Y)

Пример. Таблица распределения: Найти

X \ Y	0	1
0	1/6	2/6
1	2/6	1/6

X\Y	y≤0	0<y≤1	y>1
x≤0	0	0	0
0<x≤1	0	1/6	1/2
x>1	0	1/2	1

Решение.

0 1

С войства функции распределения: 1)

2 )

3 )

4 ) непрерывна слева по каждому из своих аргументов:

5 )

Замечание. Функция распределения двумерной непрерывной СВ является непрерывной.

№20. Плотность распределения 2-мерной СВ.

П лотностью распределения (совместной плотностью) непрерывной двумерной СВ (X,Y) называется вторая смешанная производная ее функции распределения.

П лотность распределения есть предел отношения вероятности попадания СВ (X,Y) в прямоугольник со сторонами , примыкающий к точке (x,y) к площади этого прямоугольника. Δy

Замечание. (x,y) Δx

У читывая определение, можно записать

С войства плотности распределения: 1) 2) Вероятность попадания СВ (X,Y) в область D равна

3) Свойство нормировки: 4) Плотности распределения одномерных СВ X и Y можно найти по формулам:

П ример. Плотность распределения двумерной СВ (X,Y)

Найти: A,

Реш. По св. Норм.

№21. Корреляционный момент.

К орреляционным моментом (ковариацией) двух СВ X и Y называется мат. ожидание произведения отклонений СВ от своих мат. ожиданий:

П о свойствам мат. ожидания:

С войства ковариации: 1) 2) Доказательство.

3) Если СВ X и Y независимы, то Доказательство.

Ковариация служит для качественной характеристики зависимости между СВ.

№22. Коэффициент корреляции.

Коэффициентом корреляции двух СВ X и Y называется величина

23.Основные понятия математической статистики.

Математическая статистика изучает закономерности, которым подчинены массовые случайные явления, с помощью методов ТВ.

Основные задачи мат. статистики:

— упоряд. исх. данные (представить их в виде, удоб. для анализа);

— оценить требуемые характеристики наблюдаемой СВ (функцию распределения, мат. ожидание, дисперсию и т.д.);

— проверить статистические гипотезы, т.е. решить вопрос согласования результатов оценивания с данными.

Совокупность всех подлежащих исследованию объектов называется генеральной совокупностью.

Выборочной совокупностью или случайной выборкой называют совокупность случайно отобранных объектов.

О бъемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Н аблюдаемые значения называют вариантами.

Ч исла называют частотами.

Числа называют относительными частотами.

Е сли число вариант велико или наблюдаемая СВ является непрерывной, то поступают следующим образом. Вместо значений в первую строку вариационного (статистического) ряда записывают (ф-ла Стерджеса) полуинтервалов длиной

Полученный ряд называют интервальным.

24.Полигон и гистограмма

П олигоном частот называется ломаная, соединяющая точки с координатами

П олигон частот строится на основе вариационного ряда. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников с основанием h и высотой Замечание.