6.4. Пример использования принципа особых состояний при моделировании системы

Пусть рассматриваемая система – библиотека, в которой работает один библиотекарь. Задан интервал прихода между читателями (равномерный 2-6). Задан интервал обслуживания (равномерный 3-4). Реализовать моделирование работы библиотеки по обслуживанию 100 читателей. Рассчитать среднее время ожидания в очереди и вероятность простоя библиотекаря.

1 шаг. Выберем входные, промежуточные и выходные переменные

входные и промежуточные переменные:

Т инт. прих. – интервал между приходом читателей;

Т инт. обс. – интервал облуживания читателя

Т прих. – момент прихода очередного читателя;

Т нач. обс. – момент начала обслуживания очередного читателя;

Т ок. обс. – момент окончания обслуживания очередного читателя;

выходные переменные:

Т ож. – время ожидания читателя в очереди;

Т простоя – время простоя библиотекаря до прихода очередного читателя;

Т ож.ср. – среднее время ожидания читателя в очереди;

Т простоя – суммарное время простоя библиотекаря;

Р простоя – вероятность простоя библиотекаря.

В табл. 2. и рис. 6 приведены данные ручного моделирования обслуживания первых четырех читателей для иллюстрации принципа особых состояний моделирования системы. Интервалы прихода читателей и интервалы обслуживания заданы произвольно.

Таблица 2. Имитационное моделирование обслуживания читателей

Номер шага (читателя)	T инт. прихода	T инт. обсл	T прихода	T начала. обс.	T ок. обс.	T ожидания в очереди	T простоя библиот.
1	3	4	3	3	7	0	3
2	5	3	8	8	11	0	1
3	2	4	10	11	15	1	0
4	3	4	13	15	19	2	0
…
100

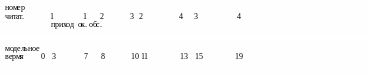
Рис. 6.

2 шаг. Разработка блок-схемы алгоритма имитации СМО (рис. 7)

3 шаг. В соответствии с разработанной блок-схемой составляется программа имитации работы СМО на любом языке программирования с использованием любых программных средств.

4 шаг. Расчет показателей эффективности СМО с помощью разработанной программы имитации.

5 шаг. Анализ полученных результатов, оценка эффективности СМО.

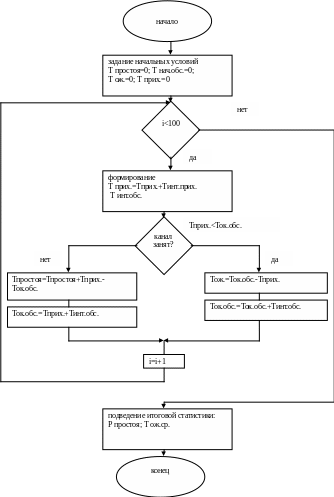
Рис. 7. Блок-схема алгоритма имитации работы СМО

7. Математические основы имитационного моделирования

7.1. Методы генерации случайных чисел

Существует три способа генерации случайных чисел:

1. Аппаратный - в основе лежит какой-либо физический эффект (например, шумы в электронных устройствах, случайные числа вырабатываются с помощью специального датчика. Этот способ не гарантирует качество последовательности случайных чисел непосредственно во время моделирования. С помощью этого способа нельзя получать одинаковые последовательности. Используется редко.

2. Табличные - случайные числа оформлены в виде таблицы в оперативной памяти или на внешнем носителе. При этом способе запас чисел ограничен, вычислительные ресурсы используются неэффективно. Используется редко.

3. Программный (алгоритмический) - случайные числа формируются с помощью специальных программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ. Этот способ наиболее распространен.

Программная имитация случайных воздействий сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Чаще всего в качестве базовой последовательности используют независимые случайные величины, равномерно распределенные на интервале (0,1).

Непрерывная случайная величина имеет равномерное распределение в интервале (a,b), если ее функции плотности и распределения соответственно примут вид

Для получения случайных чисел на ЭВМ используются алгоритмы, поэтому такие последовтельности, являющиеся по сути детерминированными, называются псевдослучайными. ЭВМ оперирует n-разрядными числами, поэтому поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2ⁿ случайных чисел того же интервала - закон распределения такой дискретной последовательности называется квазиравномерны распределением.

Требования к идеальному генератору случайных чисел:

1. Последовательность должна состоять из квазиравномернло распределенных чисел.

2. Числа должны быть независимыми.

3. Последовательности случайных чисел должны быть воспроизводимыми.

4. Последовательности должны иметь неповторяющиеся числа.

5. Последовательности должны получаться с минимальными затратами вычислительных ресурсов.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных числе находят алгоритмы вида:

x_i+1=Ф(x_i),

представляющие собой реккурентные соотношения первого порядка.

Одна из первых процедур исторически сложившихся – метод серединных квадратов.

Пример. x₀ = 0,2152 , (x₀)²=0,04631104 , x₁ = 0,6311 , (x₁)²=0,39828721, x₂=0,8287 и т.д. Пусть имеется 2n-разрядное число меньше 1, возведем его в квадрат, а затем отберем средние 2n разрядов.

Недостаток подобных методов - наличие корреляции между числами последовательности, а иногда случайность вообще отсутствует, например:

x₀ = 0,4500 , (x₀)²=0,20250000, x₁ = 0,2500 , (x₁)²=0,06250000, x₂=0,2500 и т.д.

Широкое применение получили конгруэнтные процедуры генерации псевдослучайных последовательностей.

В основе лежит понятие конгруэнтности. Два целых числа  и  конгруэнтны (сравнимы) по модулю m, где m - целое число, тогда и только тогда, когда существует такое целое число k, что -=km, т.е. если разность делится на m и если числа  и  дают одинаковые остатки от деления на абсолютную величину числа m.

Пример: =9375 и =1875: 9375-1875=7500=4*1875

9375-6875=2500=4*625.

Большинство конгруэнтных процедур генерации случайных чисел основаны на следующей формуле:

где - неотрицательные целые числа.

По целым числам последовательности {X_i} можно построить последовательность {x_i}={X_i/M} рациональных чисел из единичного интервала (0,1).

Конгруэнтная процедура получения последовательности псевдослучайных чисел квазиравномерно распределенных чисел может быть реализована мультипликативным или смешанным методом.

Мультипликативный метод.

Задает последовательность неотрицательных целых чисел {X_i} не превосходящих М по формуле:

,

где - неотрицательные целые числа.

Выражение означает: равен остатку от деления на M.

В силу детерминированности метода получают воспроизводимые последовательности.

В качестве X₀ выбирают произвольное нечетное число; М – число определяющее, наибольшее значение получаемых случайных чисел, при машинной реализации , р – основание системы счисления, g – число бит в машинном слове.

Смешанный метод.

Задает последовательность неотрицательных целых чисел {X_i} не превосходящих М по формуле:

,

где - неотрицательные целые числа.

С вычислительной точки зрения метод сложнее, но введение дополнительного параметра позволяет уменьшить возможную корреляцию между генерируемыми числами.

В настоящее время почти все библиотеки стандартных программ для вычисления последовательностей равномерно распределенных СЧ основаны на конгруэнтной процедуре.

Применяемые генераторы случайных чисел перед моделированием должны пройти тщательное предварительное тестирование на равномерность, стохастичность и независимость получаемых последовательностей случайных чисел.

Методы улучшения качества последовательностей случайных чисел:

Один из методов: использование рекуррентных формул порядка r:

Но применение этого способа приводит к увеличению затрат вычислительных ресурсов на получение чисел.