1.7. Методика вычисления коэффициентов уравнения регрессии с помощью матричной алгебры

Для решения системы дифференциальных уравнений, приведенной в предыдущем параграфе, с помощью матричной алгебры необходимо:

- представить полученные в результате опыта данные в следующем виде:

 _i = y_i - [ ₀f₀(x_i) +  ₁f₁(x_i) + ... +  _mf_m(x_i)],       i = 1, ... , s,     (1.15)

где s - число опытов в эксперименте;

- ввести и определить конструктивную (структурную) матрицу:

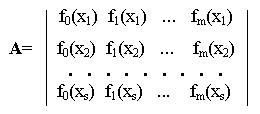
- ввести и определить транспонированную матрицу параметров:

' = ( ₀,  ₁, ...,  _m);

- ввести и определить матрицу-столбец значений y_i, i=1,...,s:

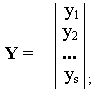
- представить систему (1.15) и функцию  в матричной форме:

(последнее уравнение получено с учетом того, что

- продифференцировать последнее выражение функции  по каждому параметру  _i , в результате чего будет получена следующая система уравнений:  

- решить данную систему, выполняя следующие действия:

Для получения решения  ^{^} необходимо, чтобы строки матрицы A' были линейно зависимы. Если при решении данной задачи использовать для представления уравнения регрессии формулу

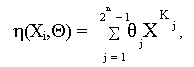  то вместо выражения f_j(x_i) можно использовать выражение X^Kj , при этом вычисления могут быть существенно упрощены.

Пример. Пусть некоторый показатель исследуемого процесса представляет собой случайную величину Y = F(x₁, x₂, x₃). Тогда функция регрессии    _i,  , представляющая собой математическое ожидание E{y_i}, i = 1,...,s, можно представить в вид полинома

   _i,  =  ₀ +  ₁x₁ +  ₂x₂ +  ₃x₃ +  ₄x₁x₂ +  ₅x₁x₃ +  ₆x₂x₃ +  ₇x₁x₂x₃ .

При этом заглавная строка структурной матрицы A будет иметь следующий вид:

x₀ , x₁, x₂, x₃, x₁x₂, x₁x₃ x₂x₃ x₁x₂x_3,

а сама матрица A, представляющая собой план проведения эксперимента, приобретает следующий вид:                              Таблица 1.1

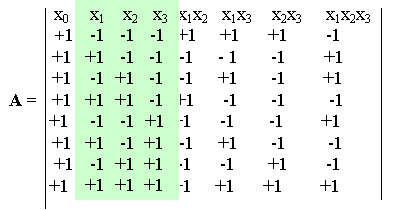
Данная таблица обладает следующими свойствами:

- добавлена фиктивная переменная x₀ для приведения свободного коэффициента  ₀ к общему виду;

- значения переменных x_j, j {0, 1, 2, 3} определены на множестве {-1, +1}, где -1 замещает наименьшее, а +1 - наибольшее значение переменной x_j из области допустимых ее значений;

- комбинации значений независимых переменных x₁, x₂, x₃ в данном случае представлены всеми возможными элементами декартового произведения {-1, +1}  {-1, +1}  {-1, +1}, которое называется полным или насыщенным планом эксперимента;

- значения таблицы, представляющие нелинейные члены полинома  ( _i, ), получаются в результате перемножения значений переменных x₁, x₂, x₃ в соответствующих столбцах таблицы;

- число строк s матрицы А соответствует наименьшему количеству опытов, необходимому для вычисления коэффициентов  (в данном примере s = 2³, что соответствует количеству искомых параметров  _j);

- матрица А должна обладать следующими свойствами:

симметричности - 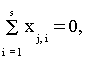                         j = 1,2,...,7,

нормализованности          -

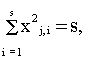
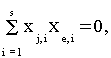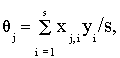ортогональности -                   e{1,...,7},  ej,  x_j,i    - функция из заглавной строки таблицы 1.1, представляющая собой комбинацию переменных x₁,x₂,x₃.   При наличии перечисленных свойств матрицы А коэффициенты  _j определяются по формуле       а дисперсия этих параметров - по формуле       ² { _j} =  ² {y_i} / s.  Приведенная методика годится для оценки параметров любой многофакторной функции    _i,  . Классическим примером применения метода максимального правдоподобия является задача определения (уточнения) параметров орбиты космического аппарата [8] .

Примечание. Использование вычислительной процедуры, реализующей метод наименьших квадратов с целью получения оценок коэффициентов модели, которые удовлетворяли бы условиям несмещенности, состоятельности и эффективности, предполагает выполнение следующих условий [9]:

* независимые переменные представляют собой неслучайный набор чисел таких, что их среднее значение и дисперсия конечны,

* случайные ошибки  _i имеют нулевую среднюю и конечную дисперсию

* между независимыми переменными отсутствует корреляция и автокорреляция,

* случайная ошибка не коррелированна с независимыми переменными,

* случайная ошибка подчинена нормальному закону распределения,

* зависимость между входными (независимыми) переменными и выходными (зависимыми) линейна.