2.2. Основные свойства преобразования Лапласа

Преобразованием Лапласа называют соотношение

(2.2.1)

ставящее функции x(t) вещественную переменную в соответствие функцию X(s) комплексную переменную s (s = s + j). При этом x(t) называют оригиналом, а X(s) - изображением или изображением по Лапласу. То, что x(t) имеет своим изображением X(s) или оригиналом X(s) является x(t), записывается так:

(2.2.2)

Иногда также пользуются символической записью

X(s) = L{x(t)}, (2.2.3)

где L - оператор Лапласа.

Предполагается, что функция x(t), которая подвергается преобразованию Лапласа, обладает следующими свойствами: x(t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0, ); x(t) = 0 при t < 0; существуют такие положительные числа М и с, что |x(t)|  Me^ct при 0  t <. Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами.

Соотношение

(2.2.4)

определяющие по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берётся вдоль любой прямой ReS  = _o>c. Символически обратное преобразование Лапласа можно записать так:

x(t) = L^-1{X(s)}, (2.2.5)

где символ L^-1 - обратный оператор Лапласа.

Основные свойства преобразования Лапласа:

1. Свойство линейности. Для любых постоянных  и 

L{x₁(t) +  x₂(t)} = L{x₁(t)} + L{x₂(t)}. (2.2.6)

2. Дифференцирование оригинала. Если производная x'(t) является функцией-оригиналом, т. е. обладает указанными выше тремя свойствами, то

L{x'(t)} = sX(s)-x(0), где X(s) = L{x(t)},

И вообще, если n-я производная x⁽ⁿ⁾(t) является функцией-оригиналом, то

L{x⁽ⁿ⁾(t)} = sⁿX(s)-s^n-1x(0)-s^n-2 x'(0)-...-x^(n-1)(0), (2.2.7)

где

Если начальные условия нулевые, т. е. x(0) = x'(0) = ... = x^n-1(0) = 0, то последняя формула принимает вид:

L{x⁽ⁿ⁾ (t)} = sⁿX(s)

Т. о., при нулевых начальных условиях дифференцированию оригинала соответствует умножение изображения на s.

3. Интегрирование оригинала. Оно сводится к делению изображения на s:

(2.2.8)

4. Теорема запаздывания. Для любого положительного числа 

L{x(t-)} = e^-s L{x(t)} = e^-st X(s) (2.2.9)

5. Теорема о свертке (теорема умножения изображения). Если x₁(t) и x₂(t) - оригиналы, а X₁(s) и X₂(s) - их изображения, то

(2.2.10)

Интеграл правой части равенства называют сверткой функций x₁(t) и x₂(t) и обозначают x₁(t)  x₂(t):

(2.2.11)

6. Теорема о предельных значениях. Если x(t) - оригинал, а X(s) - его изображение, то

(2.2.12)

и при существовании предела

(2.2.13)

имеем

(2.2.14)

7. Теорема разложения. Если функция X(s) = A(s) / B(s) дробно-рациональна, причем степень полинома числителя меньше степени полинома знаменателя, то её оригиналом является умножение на 1(t) функция

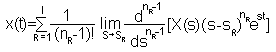(2.2.15)

где s_k -корни уравнения B(s) = 0, а n_k - их кратности и l - число различных корней. Если все корни уравнения простые, то эта формула разложения примет вид

(2.2.16)

где n - степень полинома B(s),

(2.2.17)