5.1.4. Нечёткая логика

Как и в основе теории чётких множеств лежит чёткая логика, в случае нечётких множеств существует нечёткая логика - как основа для операций. В случае двузначной чёткой логики существуют полные системы, образуемые операциями НЕ-И-ИЛИ, НЕ-И и НЕ-ИЛИ. С их помощью можно записать все другие логические операции. Но в случае нечёткой логики можно создать неограниченное число операций, поэтому нет смысла говорить о записи всех операций с помощью некоторого числа базовых операций. Поэтому рассматривают наиболее важные операции.

Рассмотрим расширения НЕ, И, ИЛИ до нечётких операций. Назовем эти расширения соответственно нечётким отрицанием, t-нормой и s-нормой. В нечётком мире число состояний неограниченно велико, поэтому невозможно описать эти операции с помощью таблицы истинности, как в случае двузначной логики. Для пояснения их используют функции и аксиомы, а представляют их с помощью графиков. Нечёткое отрицание записывают, для примера, следующим образом:

:[0, 1]  [0, 1],

0^  =  1,

(x^)^  =  x для x[0, 1] (5.1.18)

x₁ < x₂  x₁^ > x₂^,

x  =  1 – x.

Для t-нормы записывают:

T :[0, 1]  [0, 1]  [0, 1],

xT1  =  x, xT0  =  0 для x[0, 1], (5.1.19)

x₁Tx₂  =  x₂Tx₁,

x₁T(x₂Tx₃)  =  (x₁Tx₂)Tx₃,

x₁  x₂  x₁Tx₃  x₂Tx₃,

x₁ T x₂  =  x₁  x₂.

Нечёткое расширение ИЛИ - s-норма выглядит:

S :[0, 1] + [0, 1]  [0, 1],

xS1  =  1, xS0  =  x для x[0, 1], (5.1.20)

x₁Sx₂  =  x₂Sx₁,

x₁S(x₂Sx₃)  =  (x₁Sx₂)Sx₃,

x₁  x₂  x₁Sx₃  x₂Sx₃,

x₁ S x₂  =  x₁ V x₂.

Не выполняется закон комплементарности:

x  (1-x)  0, x V (1-x)  1. (5.1.21)

5.1.6. Нечёткие выводы

Нечёткие выводы - это наиболее важный метод в нечёткой логике. Выводы в чётком искусственном интеллекте охватывали как частный случай все нечёткие выводы, поэтому экспертные системы, построенные на чёткой методологии искусственного интеллекта, можно считать частным случаем нечётких экспертных систем.

Поясним на простом примере, как выполняются нечёткие выводы по правилам. Пусть существуют знания эксперта о том, что необходимо открыть спускной клапан, если уровень воды поднимается. Это знание можно представить с помощью нечёткого продукционного правила типа "если ... то ..." следующим образом:

Если уровень воды высокий, то открыть клапан. (5.1.21)

Здесь выражение, стоящее после если, называют антецедентом, предпосылкой, условием и т. п., а выражение, стоящее после то, - заключением, операцией и т. п. В нашем случае важно описать предпосылку и заключение в виде нечёткого отношения. Другими словами, в исходное выражение не попали данные о том, каков уровень воды в метрах, на какой угол поворачивать клапан. Однако сам эксперт это знает. Например, если мы спросим у него: " Высокий уровень воды - это сколько метров?" - то получим ответ: "Примерно 2 м". При этом интерпретация с помощью нечёткого множества, например

ВЫСОКИЙ = 0,1/1,5м + 0,3/1,6м + 0,7/1,7м + 0,8/1,8м + 

+ 0,9/1,9м + 1,0/2,0м + 1,0/2,1м + 1,0/2,2м (5.1.22)

гораздо более точно отражает мысль эксперта, нежели строгая интеграция его слов: "До 1,9 м ещё невысокий уровень, а начиная с 2,0 м - высокий". Аналогично угол поворота клапана, если принять 90 за полное открытие, можно описать с помощью следующей функции принадлежности:

ОТКРЫТЬ = 0,1/30 + 0,2/40 + 0,3/50 + 0,5/60 +

+ 0,8/70 + 1,0/80 + 1,0/90 (5.1.23)

Человек, проектирующий данную систему, создает из правил в словесном представлении типа (5.1.21) конкретные функции принадлежности типа (5.1.22) и (5.1.23). Обычно он следует следующему методу:

1) определяет значения методом вопросов и ответов или становится учеником эксперта;

2) поручает эксперту выполнение операции и воссоздает ситуацию из хронометрированных данных;

3) корректирует значения функции, получая наилучшие результаты из экспериментов, имитирующих данную ситуацию.

Если получить функцию принадлежности, следуя указанному выше методу, то можно запомнить их в ЭВМ как базу знаний. Например, формулы (5.1.22) и (5.1.23) можно запомнить как информацию в одномерном массиве, индексы в котором соответствуют элементам полного пространства. Без ограничения общности будем считать, что нечёткие продукционные правила типа (5.1.21) накапливаются в базе знаний. Пусть также при наблюдении текущего уровня воды обнаружено, что

Уровень воды довольно высокий. (5.1.24)

Если наблюдения уровня воды возможны с большей точностью, то можно получить точную информацию, например: "уровень воды 1,7 м". Однако на практике нередки случаи, когда из-за особенностей промышленной системы информацию с достаточно хорошей точностью получить не удается (при этом учитывается погрешность измерения, которая меняет в ту или иную сторону значение 1,7 м) либо нет возможности установить устройство измерения уровня воды и, например, этот уровень вынуждены оценивать, постукивая по ёмкости и реагируя на звук. В подобных случаях удобно принимать за информацию наблюдение (5.1.24), представленное с помощью нечёткого множества следующим образом:

Довольно ВЫСОКИЙ = 0,5/1,6м + 1,0/1,7м + 0,8/1,8м + 0,2/1,9м. (5.1.25)

Какую же операцию можно проделать в такой ситуации? Другими словами, поставим задачу: определить нечто, отмеченное знаком "?" в формуле

Если ВЫСОКИЙ, то ОТКРЫТЬ

Довольно ВЫСОКИЙ (5.1.26)

_________________________

?

Разумеется, предпосылка ВЫСОКИЙ и наблюдение "довольно ВЫСОКИЙ" обозначаются путем сопоставления. В чёткой логике сопоставление не имеет смысла, поэтому никакого логического вывода сделать нельзя. Однако мы говорим о человеке, а он, получив путем приближенного сопоставления вывод

Если ВЫСОКИЙ, то ОТКРЫТЬ

Довольно ВЫСОКИЙ (5.1.27)

_________________________

Слегка ОТКРЫТЬ,

должен слегка приоткрыть клапан. По сути, он выполнил нечёткий вывод (точнее, провел приближённые рассуждения).

Нечёткое продукционное правило

если ВЫСОКИЙ то ОТКРЫТЬ

а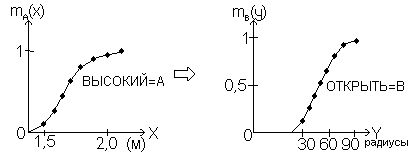

Данные наблюдения "довольно ВЫСОКИЙ"

б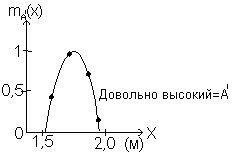

в

г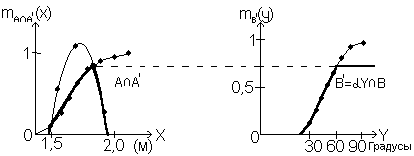

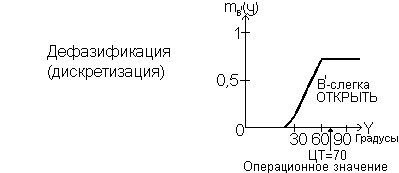
Рисунок 5.11. Пример нечётких выводов по правилам

Если говорить о мышлении человека на лингвистическом уровне, то формула (5.1.27) представляет классический пример нечёткого вывода, но какие же вычисления нужно проделать в программе или внутри специальной микросхемы нечёткого вывода, где встроены функции принадлежности? Существует более ста методов преобразования нечётких выводов на лингвистическом уровне в вычисления, но если ограничиться только методом, наиболее часто используемым на практике, то все объяснения можно привести с помощью рис. 5.11. Здесь полное пространство предпосылок - уровни воды, а полное пространство заключений - углы работы клапана. Обозначим их соответственно через X и Y. Используя формулы (5.1.22) и (5.1.23), нечёткое продукционное правило (5.1.21) можно графически изобразить так, как на рис. 5.11, а (данные между точками соответствующим образом интерполированы и показаны непрерывной линией). Кроме того, позаботимся об упрощении рассуждений и обозначим через А нечёткое множество ВЫСОКИЙ в предпосылке Х и через В нечёткое множество ОТКРЫТЬ в заключении Y. Нечёткое множество "довольно ВЫСОКИЙ" в данных наблюдениях Х (сокращенно А') из формулы (5.1.25) можно представить так, как на рис. 5.11 б. На рис. 5.11 в графически изображен процесс классического нечёткого вывода. Справа как А  А' получен результат приближенного сопоставления предпосылки правила А и данных наблюдения А'. Затем рассмотрим максимальное значение  как некую меру сопоставления А  А', выполним редукцию по этой мере заключения В в правиле и получим результат вывода В (рис. 5.11 в). В качестве способа редукции В выбрано отсечение по мере сопоставления  (на рисунке Y означает, что

m_Y(y)  =   для yY ). (5.1.28)

Итак, для текущих данных наблюдения А (=  довольно ВЫСОКИЙ) в результате применения правила А  В (=  если ВЫСОКИЙ, то ОТКРЫТЬ) получаем В (= слегка ОТКРЫТЬ). Здесь результат вывода В является нечётким множеством в Y, как показано на рис. 5.11 г. Однако пока никаких конкретных операций произвести нельзя. Дело в том, что на основе функции принадлежности m_B (y) для В необходимо ещё извлечь для каждой точки в Y значения для выполнения операции. Этот процесс обычно называют дефазификацией (т. е. преобразованием нечёткого множества в чёткое представление). На рис. 5.11 для этих целей использован метод центра тяжести (ЦТ), определено примерное значение для операции ЦТ = 70 (градусов), и принято решение повернуть клапан на 70 градусов.