3. Устойчивость линейных систем автоматического управления

3.1. Понятие устойчивости

На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить её нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

В простейшем случае понятие устойчивости системы связано с её способностью возвращаться (с определённой точностью) в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого её вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.

Наблюдения показывают, что некоторые положения равновесия системы устойчивы к небольшим возмущениям, а другие принципиально возможные равновесные положения практически не могут быть реализованы.

Наглядно устойчивость равновесия представлена на рис. 3.1, где изображён шар, расположенный в некотором углублении (рис. 3.1, а), на

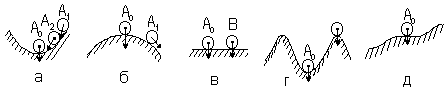
Рисунок 3.1

некоторой выпуклой поверхности (рис. 3.1, б), на плоскости (рис. 3.1, в).

Положение равновесия шара характеризуется точкой А_о. В случае, изображённом на рис. 3.1, а, при всяком отклонении шара от положения равновесия, например в точку А₁, он будет стремиться снова возвратиться к положению равновесия - в точку А_о (при отсутствии сил трения) или к некоторой конечной области, окружающей положение равновесия, например в точку А₂ (при наличии сил трения). Такое положение равновесия устойчиво. Случай, изображённый на рис. 3.1, б, соответствует неустойчивому положению равновесия. Рис. 3.1, в соответствует безразличному равновесию. На рис. 3.1, г состояние равновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определяемую, например, точкой В. Выйдя за эту границу, шар уже не вернётся в точку А_о, а будет двигаться вправо от точки В, либо всё время удаляясь, либо до нового состояния равновесия в зависимости от формы поверхности, т. е. в конечном счёте в зависимости от уравнения движения шара.

Поэтому в общем случае, рассматривая нелинейные системы, вводят понятие устойчивости “в малом”, “в большом” и “в целом”. Система устойчива “в малом”, если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом её границы. Систему называют устойчивой “в большом”, когда определены границы области устойчивости, т. е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют устойчивой “в целом”. Устойчивость “в целом” для определённого класса нелинейности называют “абсолютной” устойчивостью.

Так, например, случай, изображённый на рис. 3.1, а, соответствует устойчивости “в целом”, а случай, изображённый на рис. 3.1, г, может соответствовать либо устойчивости “в большом”, либо устойчивости “в малом”. Очевидно, что система, устойчивая “в целом”, будет устойчива “в большом” и “в малом”; система, устойчивая “в большом”, будет устойчива и “в малом”.

На рис. 3.1, д изображено ещё одно принципиально возможное для нелинейных систем состояние равновесия, которое называют полуустойчивым.

Для того, чтобы дать определение устойчивости равновесия, вводят понятие о невозмущённом состоянии равновесия, соответствующем состоянию покоя в точке А_о на рис. 3.1, а, и возмущённом состоянии, соответствующем, например, точке А₁, в которую внешняя сила привела шар и затем прекратила своё действие. Система будет устойчивой, если из возмущённого состояния она перейдёт в некоторую заданную область, окружающую невозмущённое состояние равновесия.

Понятие устойчивости можно распространить и на более общий случай, когда в качестве невозмущённого состояния рассматривают не положение равновесия системы, а её движение, например движение системы по некоторой заранее заданной траектории.

Допустим, что заданное движение системы при отсутствии возмущений должно определяться некоторым законом изменения независимых координат y₁^(t), y₂^(t), ..., y_n^(t). По аналогии со случаем равновесия положение, заданное движением, называют невозмущённым движением. Внешние возмущения, действующие на систему, вызовут отклонения действительного движения системы от заданного. Действительное движение системы называют возмущённым движением. Пусть действительное движение системы определяется независимыми координатами y₁(t), y₂(t), ..., y_n(t). В общем случае y₁(t)  y₁^ (t), y₂(t)  y₂^ (t), ..., y_n(t)  y_n^ (t).

Заданное невозмущённое движение будет устойчивым, если после приложения внешних сил (возмущений), которые затем снимают, возмущённое движение по истечении некоторого времени войдёт в заданную область |y_i(t) - y_i^ (t)|  _i, где _i = const - заданные величины, i = 1, 2, ..., n.

Чтобы проиллюстрировать сказанное, предположим, что невозмущённое движение происходит по траектории А, а возмущённое движение  по траектории Б (рис. 3.2, а). Возьмём на этих траекториях две произвольные

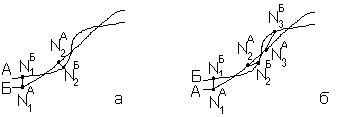
Рисунок 3.2

точки N^A и N^Б, отвечающие одному и тому же моменту времени t. При устойчивом движении траектория Б должна быть близка к траектории А. Однако близость траекторий А и Б является необходимым условием устойчивости движения, но недостаточным. Расстояние между точками N^A и N^Б, отвечающими одному и тому же моменту времени, может возрастать не только для расходящихся, но и для близких траекторий (рис. 3.2, б).