2.6.5. Форсирующее звено

Форсирующим звеном или форсирующим звеном первого порядка называют звено, которое описывается уравнением

y = k(Tp + 1)u,

или, что то же, передаточной функцией

W(s) = k(Ts + 1).

Это звено, как и апериодическое, характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом k.

Частотная передаточная функция

W(j) = k(Tj + 1).

Остальные частотные и передаточные функции имеют вид:

U() = k, V() = kT, , () = arctgT,

, h(t) = k[T(t) + 1(t)], (t) = k[T'(t) + (t)],

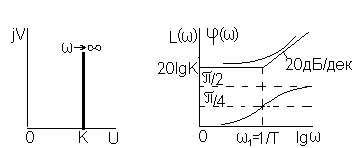
а б

Рисунок 2.8

АФЧХ (рис. 2.8, а) - это прямая, параллельная мнимой оси и пересекающая действительную ось в точке U = k. ЛАЧХ изображена на рис. 2.8, б. Как и в случае апериодического звена на практике ограничиваются построением асимптотической ЛАЧХ. Частоту ₁ = 1/T, соответствующую точке излома этой характеристики, называют сопрягающей частотой.

Уравнение асимптотической ЛАЧХ форсирующего звена имеет вид

Асимптотическая ЛАЧХ при < ₁ параллельна оси частот и пересекает ось ординат при L = 20lgk, а при ₁ имеет наклон 20дБ/дек.

ЛФЧХ форсирующего звена можно получить зеркальным отражениям относительно оси частот ЛФЧХ апериодического звена для её построения можно пользоваться теми же шаблоном и номограммой.

2.6.6. Колебательное, консервативное и апериодическое второго порядка звенья

Звено, которое можно описать уравнением

(T²₀p² + T₁p + 1)y = ku

или

(T²p² + 2Tp + 1)y = ku,

где

T = T₀,  = T₁/2T, или передаточной функцией

называют колебательным, если 0 < < 1, консервативным, если  = 0 (T₁ = 0), и апериодическим звеном второго порядка, если 1. Коэффициент  называют коэффициентом демпфирования.

2.6.7. Колебательное звено ( 0 < < 1)

Частотная передаточная функция

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю выражение, получим вещественную и мнимую частотные функции

,

Фазовая частотная функция, как видно из рис. 2.9, а АФЧХ, изменяется монотонно от 0 до - и выражается формулой

а б в

Рисунок 2.9

ЛФЧХ (рис. 2.9, б) при асимптотически стремится к оси частот, а при  - к прямой 

Амплитудная частотная функция

и логарифмическая амплитудная функция

Уравнение асимптотической ЛАЧХ имеет вид

где ₁ = 1/T, ₁ - сопрягающая частота. Асимптотическая ЛАЧХ (рис. 2.9, б) при < ₁ параллельна оси частот, а при ₁ имеет наклон -40дБ/дек.

Решением уравнения (T²₀p² + T₁p + 1)y = ku колебательного звена при u = 1(t) и нулевых начальных условиях (y(0) = y'(0) = 0). И найдем переходную функцию.

где

Весовая функция

По переходной характеристике (рис. 2.9, в) можно определить параметры колебательного звена следующим образом. Передаточный коэффициент k определяют по установившемуся значению, h() переходной функции. Постоянную времени Т и коэффициент демпфирования  можно найти из уравнений

T_к = 2, A₁/A₂ = e^Tк

или

 = 2/T_к,  = 1/T_кlnA₁/A₂,

где Т_к - период колебаний, А₁ и А₂ - амплитуды двух соседних колебаний относительно установившегося значения (рис. 2.9, в).

2.6.8. Консервативное звено ( = 0 )

Передаточная функция

W(s) = k/(T²s² + 1).

Частотная передаточная функция

W(j) = k/(1-T²²)

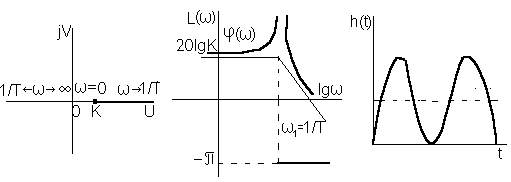
а б в

Рисунок 2.10

Фазовая частотная функция, как это следует из АФЧХ (рис. 2.10, а)

ЛЧХ приведены на рис. 2.10, б.

Переходная функция

h(t) = k(1-cos₁t), ₁ = 1/T.

Переходная характеристика (рис. 2.10, в) представляет собой график гармонических колебаний.