
- •Дифференциальное уравнение: его порядок и степень, общее и частное решения. Теорема существования и единственности дифференциального решения.
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10
- •Вопрос 14
- •Вопрос 15
- •16.Решение неоднородных дифференциальных уравнений второго порядка методом вариации вариации постоянных.
- •17. Решение линейный неоднородны дифференциальных уравнений второго порядка методом неопределённых коэффициентов.
- •18. Механические колебания: а) свободные колебания б) вынужденные колебания с) резонанс
- •19. Системы дифференциальных уравнений. Нормальная форма. Сведение нормальной системы к одному уравнению. Метод подстановки.
- •20. Системы линейных дифференциальных уравнений. Определитель Вронского системы.
- •Решение системы линейных диффер. Уравнений через собственные векторы и значения матрицы.
- •Числовой ряд. Общий член ряда. Сумма ряда. Сходимость ряда. Свойства сходящихся рядов. Остаток ряда.
- •Признак сходимости числового ряда. Гармонический ряд.
- •Знакоположительные числовые ряды. Признак сравнения (2 формы).
- •Знакоположительные числовые ряды. Признак Даламбера.
- •30)Признак Лейбница сходимости знакочередующегося числа ряда. Схема исследования на абсолютную и условную сходимость
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •37.Формула Эйлера.
- •Вопрос 38. Разложение в ряд маклорена
- •Вопрос 42.
- •Вопрос 43.
- •Вопрос 44.
- •Вопрос 46.
- •Вопрос 47.
- •Вопрос 48.
- •Вопрос 50.
Вопрос 14
ЛОДУ 2-го порядка с постоянными коэффициентами. Характеристическое уравнение. Структура общего решения.
Частный случай ЛОДУ – ЛОДУ с постоянными коэфф.
y’’+py’+qy=0 – ЛОДУ второго порядка, где p и q постоянны.
Будем искать частные решения в виде y=ekt , где k – некоторое число предложенное Эйлером. Дифференцируя эту функцию 2 раза и подставляя выражение для y,y’,y’’ в ур-е (~), получим k2ekx+pkekx+qekx=0 т.е.
ekx(k2+pk+q)=0
или (k2+pk+q)=0
(ekx 0)
это ур-е называется характеристическим
ур=ем ДУ заменяем y’’,y’,y
соответственно на k2,k
и 1.
0)
это ур-е называется характеристическим
ур=ем ДУ заменяем y’’,y’,y
соответственно на k2,k
и 1.
Структура решения: 3 случая:
1) k1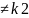 (D=
(D=
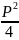 – q
>0)
– q
>0)
y1=ek1x
, y2=ek2x
.Они фундаментальную систему решений
(линейно не зависимы) т.к. их вронскиан
W(x)=
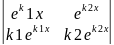 =
k2e(k1+k2)x-k1e(k1+k2)x=e(k2+k1)x(k2-k1)
0
=
k2e(k1+k2)x-k1e(k1+k2)x=e(k2+k1)x(k2-k1)
0
Общее решение имеет вид y=C1ek1x+C2ek2x
2) k1=k2 (D= – q =0)
Y1=ek1x
y2=xek2x
Они образуют фунд. систему решений
W(x)=e2k1x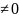
Общее решение y=C1ek1x+C2ek2xx
3) k1 и k2 комплексные корни
K1=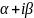 K2=
K2=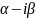 D=
– q <0,
D=
– q <0,
 ,
,
 =
=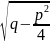 >0
>0
Общее решение имеет вид
y=eax(C1cos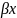 +C2sin
)
+C2sin
)
Вопрос 15
Линейные диф. уравнения 2-го порядка с правой частью. Теорема о структуре общего решения. Определение частного решения методом неопределенных коэфф.
y’’+a1(x)y’+a2(x)y=f(x) где a1(x),a2(x),f(x) непрерывные на (a,b) заданные функции.
Ур-е y’’+a1(x)y’+a2(x)y=0, левая часть которого совпадает с левой частью ЛОДУ, наз-ся соответствующим ему однородным ур-ем.
*ТЕОРЕМА О СТРУКТУРЕ ОБЩЕГО РЕШЕНИЯ: Общее решение ур-я ~ является сумма его произвольного частного решения yч и общего решения yо=C1ek1x+C2ek2x т.е. y=yч+уо
Определение частного решения методом неопр. коэфф.
Рассмотрим ЛНДУ 2-го порядка с постоянными коэфф.
Y’’+py’+qy=f(x) p и q – некоторые числа
1) f(x)=Pn(X)eax;2) f(x)=eax(Pn(x)cos +Qm(x)sin ) – специальный вид правой части.
Случай 1:
f(x)=Pn(x)eax,
где
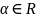 ,Pn(x)
– многочлен степени n.
,Pn(x)
– многочлен степени n.
Y’’+py’+qy= Pn(X)eax
Y*=x2Qn(x)eax
r
– число показывающие, сколько раз
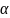 является корнем характеристического
ур-я k2+pk+q=0
(?)
является корнем характеристического
ур-я k2+pk+q=0
(?)
Qn(x)=A0xn+A1xn-1+…An – многочлен степени n, записанный с неопр. координатами Ai – (i=1,2,…,n)
Случай 2: Y’’+py’+qy =eax(Pncos +Qmsin )
Y*=x2eax(Mlcos
+Nlsin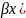 ,
r
– число, равное
,
r
– число, равное
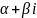 как
корня хар-го уравнения k2+pk+q=0
(?)
как
корня хар-го уравнения k2+pk+q=0
(?)
Ml и Nl – многочлены степени l с неопр. коэфф.,l – наивысшая степень многочленов Pn(x) и Qn , т.е. l=max(n,m)
Замечание: 1) После
подстановки в фун-ии приравниваем
многочлены, стоящие перед одноименными
тригонометр. функциями в левой и в правой
частях уравнения. 2) Форма сохраняется
в случаях, когда Pn(x)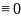 или Qn(x)
.
3) Если правая часть ур-ия f(x)
есть сумма функций вида 1 или 2,то для
нахождения y*
необходимо использовать теорему о
нахождении решения.
или Qn(x)
.
3) Если правая часть ур-ия f(x)
есть сумма функций вида 1 или 2,то для
нахождения y*
необходимо использовать теорему о
нахождении решения.
16.Решение неоднородных дифференциальных уравнений второго порядка методом вариации вариации постоянных.
y”+a1y’+a2y=f(x)
y”+a1y’+a2y=0
y1,y2
W= ≠0
≠0
y=C1(x)y1+C2(x)y2
y’=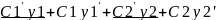
C1’y1+C2’y2=0
y’=C1y1’+C2y2’
y”=C1’y1’+C1y1”+C2’y2’+C2y2”
C1’y1’+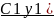 +C2’y2’+C2y2”
+a1(C1y1’+C2y2’)+a2(C1y1+C2y2)=
+C2’y2’+C2y2”
+a1(C1y1’+C2y2’)+a2(C1y1+C2y2)=
=C1(y1”+a1y1+a2y1)+C2(y2”+a1y2’+a2y2)+(C1’y1’+C2’y2’)=f(x)
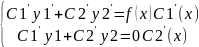 всегда
имеет решение
всегда
имеет решение
С1’(x)=….dC1/dx=….
C2’(x)=…. dC2/dx=….
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
![]()
Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение
![]()
удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:

