
- •Дифференциальное уравнение: его порядок и степень, общее и частное решения. Теорема существования и единственности дифференциального решения.
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10
- •Вопрос 14
- •Вопрос 15
- •16.Решение неоднородных дифференциальных уравнений второго порядка методом вариации вариации постоянных.
- •17. Решение линейный неоднородны дифференциальных уравнений второго порядка методом неопределённых коэффициентов.
- •18. Механические колебания: а) свободные колебания б) вынужденные колебания с) резонанс
- •19. Системы дифференциальных уравнений. Нормальная форма. Сведение нормальной системы к одному уравнению. Метод подстановки.
- •20. Системы линейных дифференциальных уравнений. Определитель Вронского системы.
- •Решение системы линейных диффер. Уравнений через собственные векторы и значения матрицы.
- •Числовой ряд. Общий член ряда. Сумма ряда. Сходимость ряда. Свойства сходящихся рядов. Остаток ряда.
- •Признак сходимости числового ряда. Гармонический ряд.
- •Знакоположительные числовые ряды. Признак сравнения (2 формы).
- •Знакоположительные числовые ряды. Признак Даламбера.
- •30)Признак Лейбница сходимости знакочередующегося числа ряда. Схема исследования на абсолютную и условную сходимость
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •37.Формула Эйлера.
- •Вопрос 38. Разложение в ряд маклорена
- •Вопрос 42.
- •Вопрос 43.
- •Вопрос 44.
- •Вопрос 46.
- •Вопрос 47.
- •Вопрос 48.
- •Вопрос 50.
Дифференциальное уравнение: его порядок и степень, общее и частное решения. Теорема существования и единственности дифференциального решения.
Дифф. Уравнение – уравнение, связывающее независимую переменную, неизвестную функцию и ее производную.
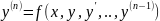 явная форма задания
диф. ур.
явная форма задания
диф. ур.
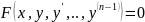 неявная форма задания
диф. ур.
неявная форма задания
диф. ур.
Порядок дифференциального уравнения – это порядок наивысшей производной, содержащийся в уравнении. y’’+y= 0 – ур-е 2-го порядка.
Степень дифференциального уравнения – наибольший показатель степени при старшей производной.
Общее решение дифф. уравнения – решение, содержащие произвольные постоянные.
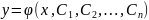 явный вид.
явный вид.
Частное решение – решение при определенных значениях произвольных постоянных.
Теорема о существовании и единственности решения.
Если функция f
непрерывна в окрестности начальных
значений и непрерывны её частные
производные, начиная с y
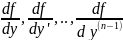 , то уравнение имеет единственное
решение, удовлетворяющее данным условиям.
, то уравнение имеет единственное
решение, удовлетворяющее данным условиям.
Дифференциальное уравнение с разделяющимися переменными.
Рассмотрим дифф. уравнение вида:
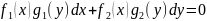
В нем одно слагаемое зависит только от х, а другое только от у. Такие уравнения называют Дифф. уравнения с разделяющимися переменными.
Перенесем первое слагаемое
направо и разделим обе части на
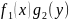 ,
получим:
,
получим:
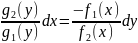
Уравнение с разделенными переменными.
Однородные дифференциальные уравнения первого порядка.
Функция f(x,y) называется однородной нулевого измерения, если выполняется условие:
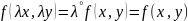
Пример:
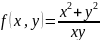
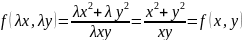
Дифф. уравнение однородно, если функция f(x,y) однородная нулевого измерения.
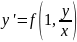
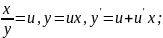
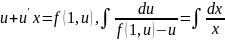

Линейные дифференциальные уравнения первого порядка.
Дифференциальное уравнение называется линейным, если оно имеет вид
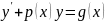
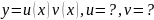
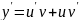
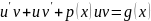
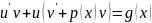
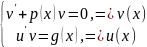
Дифференциальные уравнения Бернулли.
Уравнения Бернулли:
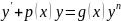 .
.
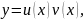
Далее как в линейных дифференциальных уравнениях:
Вопрос 6
Уравнения в полных дифференциалах
P(x,y)dx+Q(x,y)dy=0. Если выполн условие dp/dy=dq/dx
du=P(x,y)dx+Q(x,y)dy
du=0
u(x,y)=c u=?
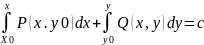
Пример: (2y-3)dx+(2x+3y^2)dy=0
P(x,y)=2y-3 dp/dy=2
Q(x,y)=2x+3y^2 dq/dx=2
Dp/dy=dq/dx=2
Это уравнение в полных дифференциалах
O(0.0)
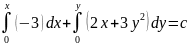
Вопрос 7
Приближенные методы решения дифф. ур-й 1-го порядка.
Графический метод.
Y’=f(x,y)
yIx=x0=y0
M0(x0.y0)
Y’(x0)=f(x0,yo)=ON0
М0(x0,y0)
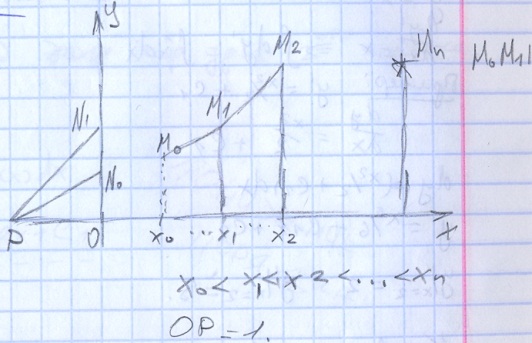
Tga0=ON0/OP=ON0
M1(x1,y1)
Y’(x1)=f(x1,y1)=ON1
M1M2IIPN1
Численное решение
y-y0=k(x-x0) - уравнение пучка прямых K=f(x0,y0)
1)M1(x1,y1) y1-y0=F(x0,y0)(x1-x0) Y1=y0+f(x0,y0)(x1-x0)
2)y2-y1=f(x1,y1)(x2-x1) y2=……
Оба метода-методы Эйлера!!
Вопрос 8.
Геометрический смысл дифф. Уравнений первого порядка. Изоклины. Поля направлений.
Геометрический
смысл уравнения первого порядка. Уравнение
(6)
![]() в каждой точке (x, y) области D,
в которой задана функция f(x, y),
определяет
в каждой точке (x, y) области D,
в которой задана функция f(x, y),
определяет ![]() -
-![]() угловой коэффициент касательной к
решению, проходящему через точку (x, y),
т.е. направление, в котором проходит
решение через эту точку. Говорят, что
уравнение (6) задаёт в D поле
направлений. График любого решения
дифференциального уравнения (называемый
также интегральной
кривой)
в любой своей точке касается этого поля,
т.е. проходит в направлении, определяемом
полем. Интегрирование дифференциального
уравнения геометрически означает
нахождение кривых, у которых направление
касательной в каждой точке совпадает
с направлением поля. На рисунке справа
изображено поле направлений, определяемое
уравнением
угловой коэффициент касательной к
решению, проходящему через точку (x, y),
т.е. направление, в котором проходит
решение через эту точку. Говорят, что
уравнение (6) задаёт в D поле
направлений. График любого решения
дифференциального уравнения (называемый
также интегральной
кривой)
в любой своей точке касается этого поля,
т.е. проходит в направлении, определяемом
полем. Интегрирование дифференциального
уравнения геометрически означает
нахождение кривых, у которых направление
касательной в каждой точке совпадает
с направлением поля. На рисунке справа
изображено поле направлений, определяемое
уравнением ![]() ,
и три интегральные кривые (три частных
решения) этого уравнения. Решение можно
провести через любую точку области D;
единственное решение можно выделить,
если задать точку, через которую проходит
интегральная кривая:
,
и три интегральные кривые (три частных
решения) этого уравнения. Решение можно
провести через любую точку области D;
единственное решение можно выделить,
если задать точку, через которую проходит
интегральная кривая:
![]()
![]() .
Для
изображения поля направлений, задаваемого
дифференциальным уравнением, рассматривают
линии уровня функции f(x, y),
т.е. геометрические места точек, в которых
касательные к интегральным кривым
сохраняют постоянное направление. Такие
линии называются изоклинами.
С помощью изоклин можно приближённо
изобразить интегральные кривые.
Для
примера построим изоклины уравнения
.
Для
изображения поля направлений, задаваемого
дифференциальным уравнением, рассматривают
линии уровня функции f(x, y),
т.е. геометрические места точек, в которых
касательные к интегральным кривым
сохраняют постоянное направление. Такие
линии называются изоклинами.
С помощью изоклин можно приближённо
изобразить интегральные кривые.
Для
примера построим изоклины уравнения ![]() .
Перебираем различные значения
постоянной C,
строим линии уровня функции
.
Перебираем различные значения
постоянной C,
строим линии уровня функции ![]() ,
соответствующие этим значениям С (т.е.
прямые
,
соответствующие этим значениям С (т.е.
прямые ![]() ),
и на этих линиях ставим чёрточки в
направлении, определяемым значением С (
),
и на этих линиях ставим чёрточки в
направлении, определяемым значением С (![]() ,
где
,
где ![]() -
угол между чёрточкой и положительным
направлением оси Ох):
-
угол между чёрточкой и положительным
направлением оси Ох): ![]() -
ось Оу;
-
ось Оу; ![]() ;
; ![]() ;
; ![]() и
т.д. Информация о направлении интегральных
кривых, полученная из рисунка (выше
справа), достаточна, чтобы сделать
качественный вывод об их поведении:
кривые должны огибать начало координат.
Это могут быть окружности или спирали
(когда мы научимся решать дифференциальные
уравнения, мы легко установим, что это
окружности; две такие окружности
изображены пунктиром).
и
т.д. Информация о направлении интегральных
кривых, полученная из рисунка (выше
справа), достаточна, чтобы сделать
качественный вывод об их поведении:
кривые должны огибать начало координат.
Это могут быть окружности или спирали
(когда мы научимся решать дифференциальные
уравнения, мы легко установим, что это
окружности; две такие окружности
изображены пунктиром).
