Вопрос 1.

Первая задача динамики точки.

В зависимости от того, что нам известно и что необходимо найти, в динамике рассматривают две основные задачи.

    Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.

    При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

где  m  – масса точки;

        a   – ускорение точки;

        F_i  – силы, действующие на точку.

    В зависимости от способа задания движения точки, это уравнение можно записать по-разному.

    Для векторного способа задания движения

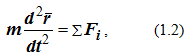
где   r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.

    Для координатного способа задания движения точки

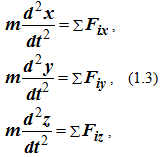
где x = x (t), y = y (t), z = z (t)  – координаты точки, заданные как функции времени.

    

Вопрос 2.

Вторая задача динамики точки. Начальные условия.

 Вторая, основная задача динамики точки заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.

    Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

    Уравнение второго основного закона динамики для материальной точки массой m запишется в виде

где a – ускорение точки;

     F_i – силы, действующие на точку, включая реакции связей. 

    Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений 

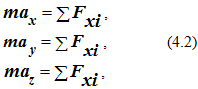
где  a_x , a_y, a_z – проекции ускорения точки на декартовы оси координат;

 F_x, F_y, F_z – проекция i -й силы на соответствующую ось.

    Учитывая, что

получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки или второго порядка относительно координат точки.

При решении этих задач необходимо ещё знать так называемые начальные условия, т. е. положение и скорость тела в момент начала его движения под действием заданных сил.

Вопрос 3.

Момент инерции механической системы и твердого тела. Радиус инерции.

Моментом инерции системы (тела) относительно оси (осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек (тел) системы на квадраты их расстояний от этой оси.

Пусть это будет ось Oz. Тогда

Осевой момент является мерой инертности системы точек (тел) при вращательном движении, размерность: в системе единиц СИ -  .

В выражении через координаты осевой момент инерции J относительно осей запишется:

Радиусом инерции тела относительно оси (Oz), называется линейная величина  , определяемая зависимостью

где М - масса тела,   - расстояние от оси Oz до точки, в которой нужно сосредоточить всю массу М тела, чтобы момент инерции этой точки относительно этой оси равнялся моменту инерции тела.

Моменты инерции относительно осей (15.3.1), зависят от выбора этих осей и относительно этих осей разные