Вопрос 5.
Естественные координатные оси. Кривизна кривой. Радиус кривизны.
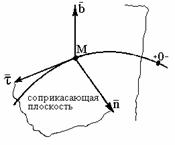
Естественными координатными осями называются три взаимноперпендикулярных оси: касательная, направленная в сторону возрастания дуговой координаты (т.е. положительного отсчета «S»); главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к касательной и главной нормали так же, как и ось OZ направлена по отношению к осям OX и OY.
Естественные координатные оси имеют начало в точке М кривой и при движении точки М по этой кривой перемещаются вместе с ней, оставаясь взаимноперпендикулярными, но изменяя свое направление в пространстве.
Кривизной К кривой в данной точке называют предел отноше-ния угла смежноcти (рис. 1.49) к длине дуги
Величина, обратная кривизне K, называется радиусом кривизны:
Вопрос 6.
Ускорение точки при задании ее движения естественным способом.
При
естественном способе задания движения
ускорение точки определяют его
составляющими, направленными по так
называемым естественным осям. Траектория
точки, как и любая кривая, имеет три
естественные оси:
- касательную (орт
оси-
)
направленную в сторону положительного
отсчета;
- главную
нормаль (орт
оси-
)
- линию пересечения соприкасающейся и
нормальной плоскостей, направленную в
сторону вогнутости кривой;
- бинормаль (орт
оси-
),
перпендикулярную касательной и главной
нормали.
Вопрос 7.
Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек при поступательном движении.
Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.
Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
Доказательство.
Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением
Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точки B – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.
Продифференцируем по времени выражение
Получаем
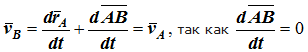
Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.
Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:
Вопрос 8.
Вращательное движение твердого тела. Уравнение вращательного движения.
Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
