Вопрос 1.

Способы задания движения точки

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета. 

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них  t.

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты:s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.

Вопрос 2.

Определение скорости и ускорения точки (векторный способ).

Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

(1)

На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M₁, а радиус-вектор получил приращение Δr. Когда Δt   0, точка M₁   M, а вектор Δr, направленный по хорде MM₁, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

По определению ускорение является производной по времени от вектора скорости:

(1)

К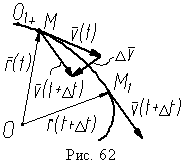 огда Δ   0, точка M₁   M; плоскость, где лежат векторы  (t),  (t + Δt) и  (Δt), содержащая две касательные к траектории в точках M и M1 (рис. 62), стремится занять положение соприкасающейся плоскости в точке M; сам вектор направлен в сторону вогнутости траектории.

Таким образом, вектор ускорения a лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории.

Очевидно, что a является ускорением в данное мгновение времени или мгновенным ускорением, а средним ускорением за промежуток времени Δt называется отношение ΔV / Δt. Соответственно, размерностью ускорения будет м / с² (метр за секунду в квадрате).

Вопрос 3.

Определение скорости точки при задании ее движения естественным способом.

При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки:

(14)

Р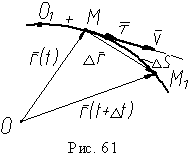 ассмотрим вектор dr / ds. Согласно формуле (14), этот вектор направлен по касательной к траектории, так как скорость направлена по касательной, а так как при Δs   0предел отношения длины дуги |Δs| к длине ее хорды MM₁ = Δr (рис. 61) равен единице, то по модулю он равен единице. Следовательно,

(15)

где   является единичным вектором касательной к траектории в точке M.

Вектор   всегда направлен в сторону возрастания дуговой координаты. На рис. 61 показан случай, когда Δs > 0 (дуговая координата точки больше координаты точки M₁). Сам вектор Δ /Δs направлен в сторону вектора Δ , в сторону положительного отсчета дуги. Когда Δs < 0 , точка M₁ будет находиться ближе к началу отсчета, чем точка M, векторΔ  изменит направление, а вектор Δ /Δs будет направлен в сторону, противоположную Δ  (Δs - отрицательное), то есть, по-прежнему, в сторону возрастания дуговой координаты.

Подставляя выражение (15) в формулу (14), получаем

(16)

Модуль вектора скорости равен V =|   |. Когда   > 0, вектор скорости направлен по вектору  , когда   < 0 , он имеет направление, противоположное вектору  .

Величину   часто называют алгебраической скоростью точки, считая ее проекцией вектора скорости на касательную к траектории точки.