8. Автоколебания в физических, химических и биологических системах. Качественное рассмотрение автоколебательных систем

Автоколебания - незатухающие колебания в диссипативных нелинейных системах, которые поддерживаются за счет внешнего источника энергии. Вид и свойства автоколебаний (частота, амплитуда, форма) определяются самой системой и не зависят от НУ. Особенность – отсутствие внешнего периодического воздействия.

Рисунок 25. Схематичное изображение автоколебательной системы

Обратная связь осуществляется через нелинейный элемент. Осциллятор сам регулирует поступление энергии от внешнего источника (отличие от вынужденных колебаний). Внешний источник определяет амплитуду, форму. Частоту. Пример автоколебаний: часы, скрипичная струна, бьющееся сердце.

Качественно е рассмотрение автоколебаний

1. Звучание скрипичной струны.

скольжения практически не зависит от скорости. Благодаря покоя струна захватывается смычком и смещается из положения равновесия. Когда , струна оторвется от смычка и устремится к положению равновесия. Скорость струны относительно движущегося смычка , и достаточная для захвата струны. Т. обр., движущийся с постоянной скоростью смычок, вызовет незатухающие колебания струны.

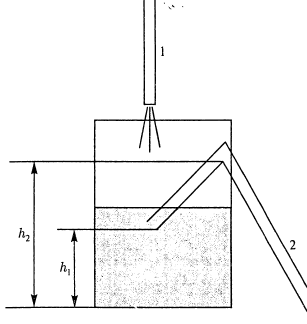2. П еремежающийся источник. Регулировка уровня воды. Пода поступает с постоянной скорость по 1. Когда уровень воды станет , вода начнет выливаться через 2, пока ее уровень не опуститься до .

3. Ч

   Рисунок 26. Перемежающийся источник.

   асы. Работа механических часов обеспечивается закрученной пружиной. Анкер – рычаг, насаженный на одну ось с маятником, - освобождает пружину 2 раза за период маятник получает толчки.

8. Самоорганизация и образование структур. Распределённые системы.

Распределенная система – система, в которой переменные изменяются в пространстве и времени.

Рассмотрим диссипативные системы – открытая система, у которой энергия упорядоченного процесса переходит в энергию неупорядоченного процесса.

Пример: Движение бруска по наклонной плоскости. Полная механическая энергия, которая при движении убывает, переходя в теплоту. Диссипации (рассеяние) механической энергии происходит вследствие наличия силы трения.

Основы теории диссипативных структур заложил в 1952 г. Алан М.Тьюринг, а термин предложил И. Р. Пригожин. Основные результаты в исследовании свойств распределенных систем получены на так называемых «базовых моделях» с двумя переменными

Формула 1. Система уравнений диффузионного типа

Данная модель качественно описывает процессы самопроизвольного возникновения волн и структур в распределенных системах, т.е. процессы самоорганизации.

Самоорганизация — процесс упорядочения элементов одного уровня в системе за счёт внутренних факторов, без внешнего специфического воздействия. Результат — появление единицы следующего качественного уровня.

Пример: Ячейки Бенара — возникновение упорядоченности в виде ячеек правильных шестигранных структур в слое вязкой жидкости равномерно подогреваемой снизу.

Общим условием развития процессов самоорганизации яв­ляется появление неустойчивости в исходной распределенной системе. Такие неустойчивости возникают, если отклонение от со­стояния равновесия превышает критическое значение.