Лекция №5. Дискретное преобразование Фурье

Содержание лекции: спектральный анализ, прямое и обратное дискретные преобразования Фурье (ДПФ), базовая операция быстрого ДПФ, алгоритмы прореживания по времени и частоте.

Цель лекции: изучить методы оценки компонентов спектра с помошью Фурье-анализа на базе применения прямого и обратного дискретных преобразований Фурье, а также алгоритмы быстрого ДПФ с прореживанем по времени и частоте, уметь оценивать их вычислительные возможности.

В ряде задач цифровой обработки необходимо оценить параметры спектра сигнала, то есть выполнить спектральный анализ. Задача спектрального анализа может носить как самостоятельный характер, например, в сейсмологии для определения типа сейсмического события или в геофизике для поиска месторождений, так и вспомогательный, например, в системах компрессии речи и изображений, компенсации помех и фильтрации.

Исходными данными для обработки являются отсчетов сигнала , то есть конечная дискретная (цифровая) последовательность как функция времени. Для исследования частотного состава этой последовательности ее нужно преобразовать, используя Фурье-анализ. С аналитической точки зрения Фурье-анализ позволяет установить связь между сигналом во временной области и его спектром в частотной области. При этом вычисляются компоненты спектра на основе дискретного преобразования Фурье (ДПФ).

ДПФ – это пара взаимно однозначных преобразований, которые в компактном виде выглядят следующим образом:

1. прямое 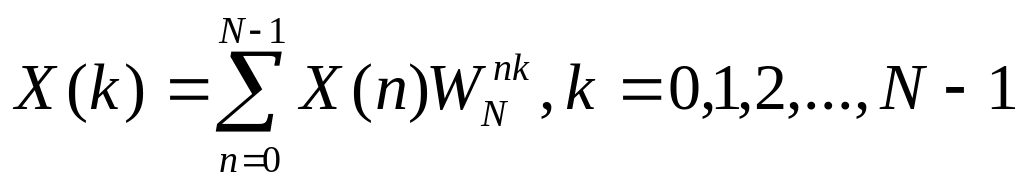, (5.1)

2. обратное 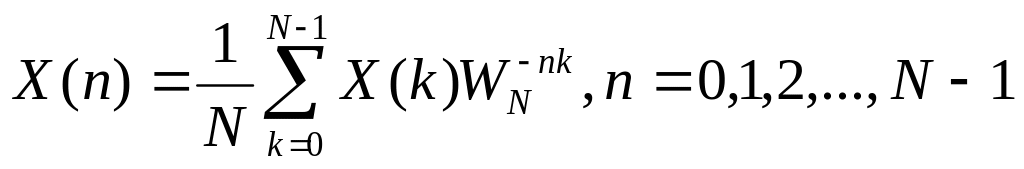(5.2)

где - длина исходной последовательности;

- количество частотных отсчетов;

- количество временных отсчетов;

- поворачивающий множитель ( весовая, периодическая функция), получивший свое название потому, что аргумент экспоненты отображает угол поворота на единичной окружности комплексной z-плоскости.

Используя свойство периодичности поворачивающего множителя можно уменьшить количество арифметических операций для вычисления ДПФ. Существует целый набор алгоритмов для быстрого ДПФ: с основанием 2, с основанием 4, Виноградова и другие.

Наибольшее распространение получили алгоритмы с основанием 2, для реализации которых длина N исходной последовательности должна быть кратна 2, т.е. , где - целое положительное число.

Первый алгоритм был опубликован в 1965 году в США и назван по имени его создателей Кули-Тьюки. Существуют две версии этого алгоритма:

1. с прореживанием по времени, при реализации которого требуется перестановка (прореживание) отсчетов входной последовательности;

2. с прореживанием по частоте, при реализации которого требуется перестановка (прореживание) отсчетов 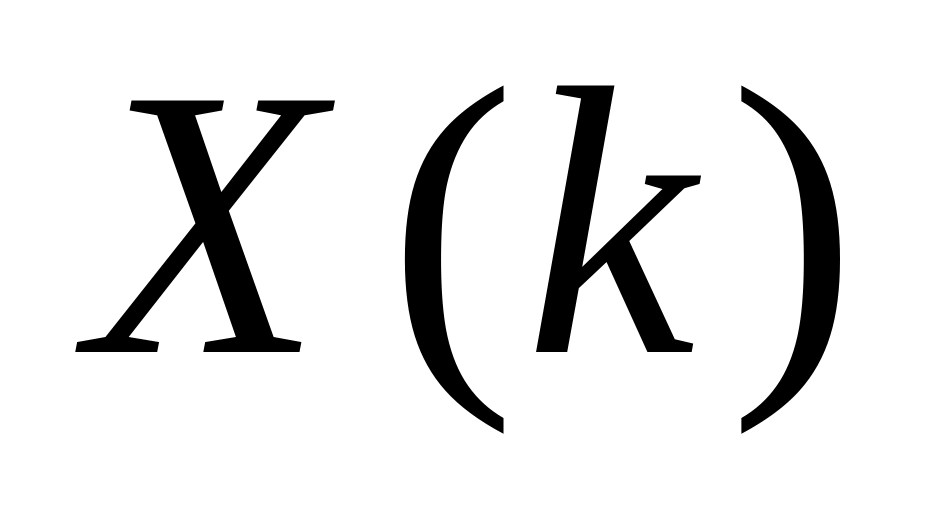выходной последовательности.

Суть первой версии в том, что N-точечное ДПФ разбивают на этапы, количество которых определяется как

На первом этапе определяются N/2 2-х точечные ДПФ, одна из которых содержит отсчеты с нечетными номерами, а другая – с четными. Тогда, сумму, представленную в формуле (5.1), можно разбить на две

, (5.3)

где ;

X(2n) и X(2n+1) – N/2 - точечные последовательности четных и нечетных отсчетов соответственно.

Поскольку 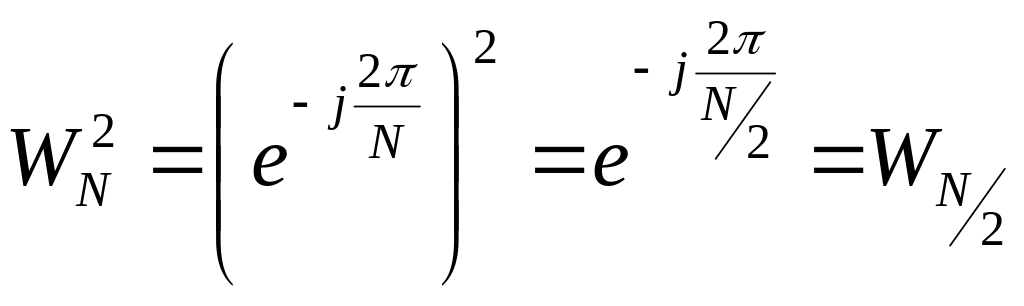получаем

. (5.4)

Учитывая, что периодично с периодом точек, получаем

, (5.5)

где .

Тогда ДПФ исходной последовательности преобразуется в два - точечного ДПФ:

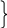
(5.6)

Представленные соотношения описывают базовую операцию быстрого преобразования Фурье (БПФ), которая называется «бабочка». Графически эту операцию можно представить в виде направленного графа который показан на рисунке 8.

Рисунок 8

Направленный граф, представленный на рисунке 8 - это структура алгоритма для 2-х точечного ДПФ, при этом . На втором этапе определяются N/4 4-х точечные ДПФ, на третьем этапе – N/8 8-и точечные ДПФ и т.д.

Перед первым этапом N-точечная последовательность должна подаваться не в естественном, а в двоично-инверсном порядке, что обеспечивает начальные условия алгоритма. В таблице 3 представлен двоично-инверсный порядок для N=8.

Т а б л и ц а 3

Естественный порядок	000	001	010	011	100	101	110	111
Двоично-инверсный порядок	000 (0)	100 (4)	010 (2)	110 (6)	001 (1)	101 (5)	011 (3)	111 (7)

На рисунке 10 показана схема формирования 8-точечного (N = 8) БПФ.

Двоично- после после после

инверсная первого второго третьего

Исходная этапа этапа этапа

X(0)

X(1)

X(2)

X(3)

X94)

X(5)

X(6)

X(7)

X(0)

X(4)

X(2)

X(6)

X(1)

X(5)

X(3)

X(7)

X₀(0)

X₀(1)

X₁(0)

X₁(1)

X₂(0)

X₂(1)

X₃(0)

X₃(1)

X₀(0)

X₀(1)

X₀(2)

X₀(3)

X₁(0)

X₁(1)

X₁(2)

X₁(3)

W⁰

W¹

W⁰

W¹

X₀(0)

X₀(1)

X₀(2)

X₀(3)

X₀(4)

X₀(5)

X₀(6)

X₀(7)

W⁰

W¹

W²

W³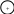

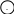
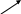
Рисунок 10

Как видно из рисунка 2 для формирования 8-точечного БДПФ нужно ДПФ разбить на три этапа, так как причем первый этап будет содержать четыре бабочки при , второй этап четыре бабочки при и , третий этап также четыре бабочки при , , , . На выходе алгоритма получается 8-точечное ДПФ, отсчеты которого следуют в естественном порядке.

Вычисления в алгоритме с прореживанием по времени можно выполнить по способу с замещением. Входная последовательность располагается в массиве из N ячеек. После вычислений на первой ступени, отсчеты входного сигнала становятся не нужными и в указанные ячейки могут быть записаны выходные данные «бабочек». На следующей ступени вновь вычисляемые значения выходов «бабочек» записываются в исходный массив и т.д. В конце вычислений в исходном массиве оказываются значения компонент спектра X(k), расположенные в естественном порядке следования их номеров, то есть значения ДПФ_N при k = 0,1,2,…, N-1.

Реализация алгоритма БПФ с прореживанием по частоте также выполняется по этапам, но в обратном направлении, то есть в сторону вдвое большей размерности ( … 8 → 4 → 2 ). При этом перед первым этапом отсчеты N-точечной последовательности не переставляются, сохраняя естественный порядок номеров ( n = 0,1,…,N-1). Однако, на выходе алгоритма получается ДПФ, отсчеты которого следуют в двоично-инверсном порядке двоичных номеров.

На практике алгоритм БПФ с прореживанием по частоте применяют реже, чем с прореживанием по времени, так как последний обеспечивает естественный порядок следования отсчетов ДПФ на выходе.

Порядок вычислительной сложности алгоритма БПФ оценивается как , в то время как при прямом вычислении ДПФ он равен . В таблице 4 наглядно представлена оценка получаемого выигрыша в объеме вычислений в зависимости от длины N исходной последовательности.

Т а б л и ц а 4

	Оценка вычислительной сложности		Оценка выигрыша
	Прямое вычисление ДПФ	Вычисление с помощью БПФ
8	64	24	2,7
16	256	64	4,0
32	1024	160	6,4
64	4096	384	10,7
128	16384	896	18,3
256	65536	1024	32,0
512	262144	4096	56,9
1024	1048576	10240	102,4