26. Способы отбора ед-ц в выборочную сов-сть.

Для того чтобы по выборке можно было сделать вывод о св-вах генеральной сов-сти, выборка д б репрезентативной. Т.е. она должна наиболее полно и адекватно представлять св-ва генер сов-сти.

Репрезентативность выборки м б обеспечена только при объективности отбора данных.

Возможны 3 способа отбора:

1)Случайный отбор;

2)Отбор по определенной схеме;

3)Сочетание первого и второго способов.

Если отбор в соотв-вии с принятой схемой произв-ся из генер сов-сти, предварительно разделенной на типы, то выборка наз типич или стратифициров.

Другое деление выборки по видам опред-ся тем, что явл-ся единицей отбора: либо это единица наблюдения, либо серия единиц (серийная выборка).

В мат ст-ке обяз-но вводят деление выборки на повторную и бесповторную. Первая осущ-ся по схеме возврат шара; вторая – безвозвратного шара (шар выним из корзины и обратно туда не возвращ).

В соц-экон ст-ке нет смысла применять повторную выборку, поэтому как правило имеется в виду бесповторный отбор.

Поскольку соц-эк объекты имеют сложную стр-ру, то выборку бывает довольно трудно орг-ть, поэтому применяют многоступенчатую выборку, в кот на каждой ступени исп-ся разные единицы отбора: более крупные – на нач ступенях, на последней ступени – единица отбора совпадает с единицей наблюдения.

Исп-ся многофазовая выборка, включ определенное кол-во фаз, каждая из кот отличается подробностью программы наблюдения.

27. Ошибки выборочного наблюдения.

Ошибка выборки или ошибка репрезентативности –разница между знач пок-ля, получ на выборке, и генеральным параметромом. Расчет ошибок позволяет решить одну из главных про­блем орг-ции выбороч наблюд — оценить реп­резентативность (представительность) выбороч сов-­сти. Различают среднюю и предельную ошибки выборки. Эти 2 вида связаны след соотношением: , где Δ-предельная ошибка выборки;t-коэф-т доверия. Определяемв завсим-ти от ур-ня вероятности;S_x-средняя ошибка выборки

Величина ср ошибки выборки рассчит дифференцир в завис от способа отбора и процеду­ры выборки. Так, при случайном повторном отборе ср ошибка опред по ф-ле: . При бесповторном: где σ²— выборочная (или генеральная) дисперсия; σ— выбо­рочное (или генеральное) среднее квадратическое отклоне­ние; n- объем выборочной совокупности; N — объем гене­ральной сов-сти.

Расчет ср и предельной ошибок выборки позвол опр возможные пределы, в кот будут нах-ся хар-ки генер сов-ти.Н-р, для выбор средней такие пределы устан-ся на основе соотношений: , где μ и х¯-генер и выборочная средние соответственно,Δ_х — предельная ошибка выборочной средней.

Для типич выборки ср ошибка вычисл по ф-лам:

-при отборе, пропорциональном объёму типич групп

(повторный отбор) 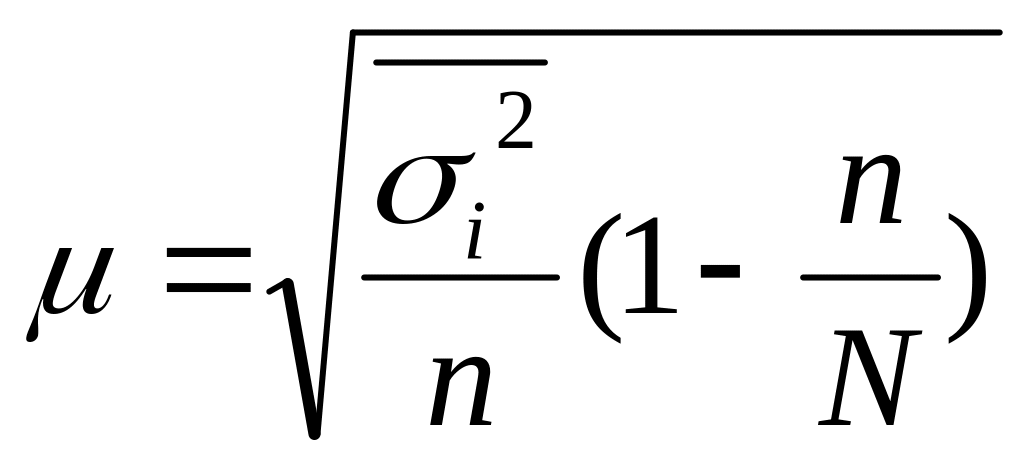(бесповторн)

-при отборе, пропорциональ вариации признака(не пропорцион-ных объёму групп)

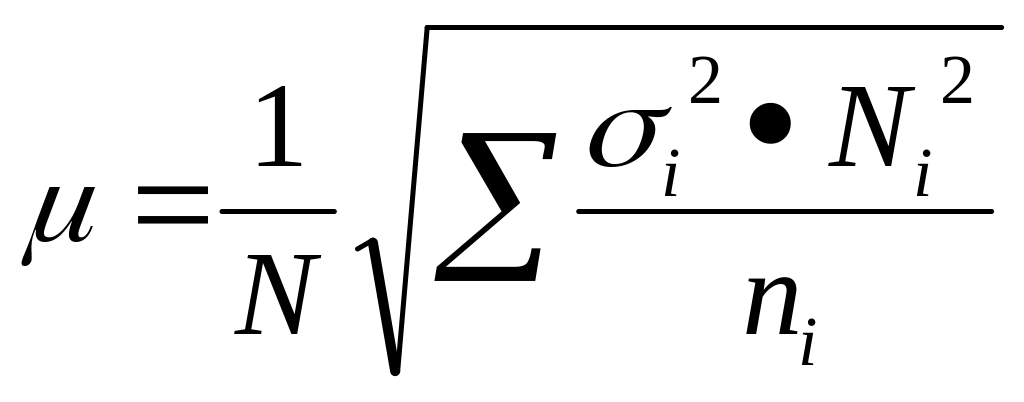(повт) 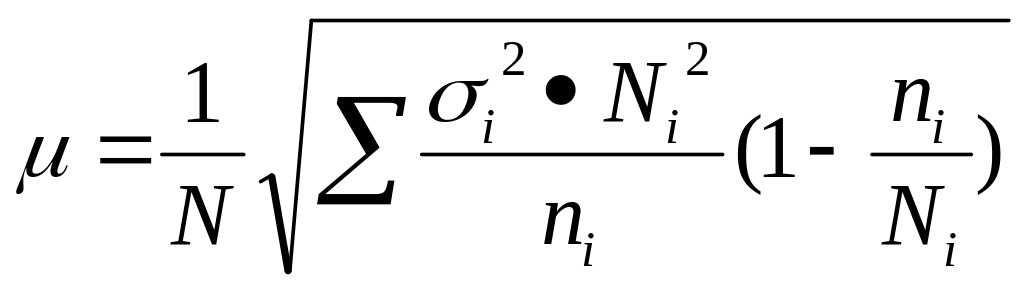(бесп)

При серийной выборке ср ошибка опр-ся след обр:

(повт) (бесп) Где R-число серий в генер сов-ти;r-число серий в выборочной сов-ти; σ²- межгруп дисперсия

28. Определ. Необх. Численности выборки

Прежде чем приступить к проведению выборочного наблюдения, надо установить необходимую численность выборки, т.е. объем выборки, необходимый для того, чтобы обеспечить результаты выборочного наблюдения с заранее установленной точностью.

Необходимая численность выборки (n) определяется на основе формул предельной выборки. Так, если выборка повторная, то n определяется из формулы , где t-коэфф. доверия. Чтобы найти необход. числ-ть выборки (n), нужно выразить ее из предыд-ей фор-лы, т.е.

n=(t²*б²)/r². Для бесповторного отбора численность выборки опред-ся из фор-лы: . Необходимая численность выборки находится путем выражения n из пред-щей фор-лы:

n = (t² * б² * N) / (r²* N + t² * б²), где n – объем выборки, N – объем генер. сов-ти.