23.Дисперсия, ее св-ва и методы расчета. Дисперсия альтернативного признака.

Дисперсия –ср квадрат отклонения всех значений признака ряда распределения от ср. арифметической. Обозначается дисперсия буквой , где х_i – индивид значение признака (варианта), х – ср. арифм-ая, n – численность сов-ти. Данная ф-ла явл простой. Взвешенная фор-ла дисперсии будет иметь вид: , где х_i – индивид значение признака (варианта), х – ср. арифм-ая, f – число единиц сов-сти с одним и тем же значением признака.

Св-ва дисперсии. 1. б²(а) = 0 – дисперсия постоянной величины равна нулю. 2. б²(а+х) = б²(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б²(ах) = а² * б²(х) – постоянный множитель выносится за знак дисперсии возведенным в квадрат. Или: если все варианты умножить на число а, дисперсия увеличится в а² раз. 4. - это св-во носит название св-ва min-ти дисперсии от средней. Дисперсия от средней меньше, чем средний квадрат отклонения от любого числа х₀ на (х₀ – х)².

Исп-ние св-в дисперсии позвол упрощать ее расчеты, особенно в тех случаях, когда вариац ряд сост арифм прогрессию или имеет равные интервалы. В этих случаях сначало находят дисперсию от условн нуля, а затем использ 4-е св-во дисперсии, переходят к дисперсии от средней.

24.Правило сложения дисперсий и его использование в анализе взаимосвязей.

Если данн представ в виде аналит группировки, то можно вычисл дисперсию общ, межгрупповую и внутригрупповую. Общ дисперсия измеряет вариацию признака во всей сов-ти под влиянием всех факторов, обуславлив эту вариацию. (1) (2)

Межгруп дисперсия хар-ет систематич вариацию, т.е. различия в величине изуч признака, воз­ник под влиянием признака-фактора, положен в основание группировки. Она рассчит по формуле 2:

Внутригруп дисперсия отражает случайную вариа­цию, т.е. часть вариации, происходящую под влиянием неуч­тенных факторов и не зависящ от признака-фактора, поло­женного в основание группировки. Она исчисляется след обр:

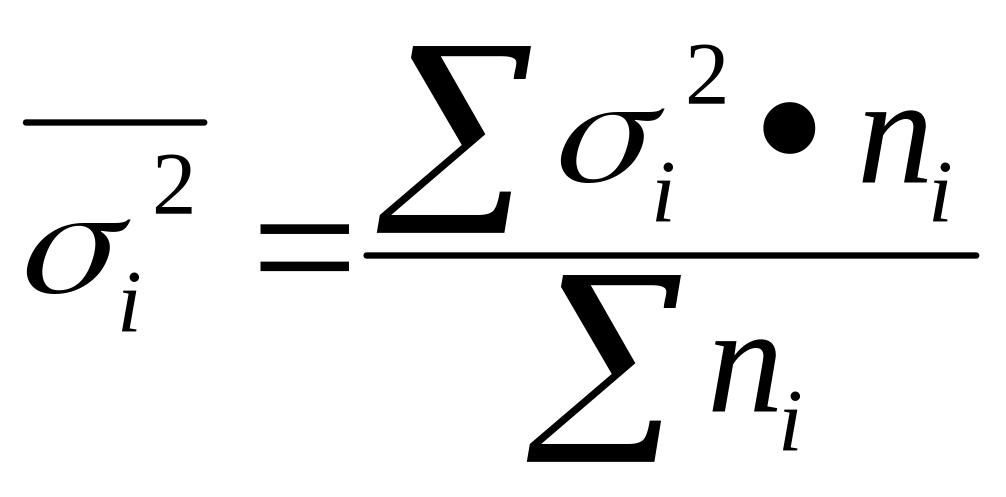(3) (4)

Средняя из внутригрупповых дисперсий (4):

Сущ-ет закон, связ три вида дисперсий. Об­щая дисперсия равна сумме средней из внутригруп и межгрупповых дисперсий: σ² =δ_х²+σ¯_i² Данное соотнош наз правилом слож дис­персий. Согласно этому правилу общая дисперсия, возник под влиянием всех факторов, равна сумме дисперсий, воз­ник под влиянием прочих фак-в, и дисперсии, возник за счет группир пр-ка.

Зная любые два вида дисперсий, можно опр или проверить правильность расчета третьего вида.

На основании правила сложения дисперсий можно опр показатель тесноты связи между группировоч (факторным) и результат при-ми. Он наз-ся эмпирическим корреляционным отношением и рассчитыва­ется по формуле:

25. Понятие о выборочном наблюдении. Причины его применения и преимущества.

Причины:

1)Выборочное наблюдение позволяет увеличить точность регистрируемых данных.

2)Экономия материальных, трудовых, финансовых ресурсов и времени.

3)Применяются в иссл-нии кач-ва продукции.

При выбороч методе наблюдению подверг не вся сов-сть единиц, а только часть их, отобранная на основе опредх научных принципов. Сущность выборочного метода: данные, получ на основе отобранной части совок-ти, распростр на всю генер. совок-ть. Ср и относ-ые величины, полученные по отобранной части единиц, достаточно точно воспроизводят соотв-щие показатели сов-сти в целом. Эта особенность выборочного метода позволяет исп-ть его с целью экономии затрат времени и труда. Кроме того, выборочное наблюд. дает возможность значительно расширить программу стат наблюд. и делать его более детальным, т.к. исслед подверг сравнительно небольшая часть совок-ти. Выборочное наблюд. находит широкое применение во всех отраслях хоз. деят-ти, в том числе и т-ле (выявл покупат спрос, провер нормы естеств убыли т-ов и др.). Также трактовка данных как выборочных явл. основой деления стат-ки на описат-ую, дискриптивную и выводную. Выборочные показатели, кот. рассм. как оценки генер-ых параметров, обознач. латинскими буквами (ср. велич. – х, относ. велич. – р, дисперсия – S², объем сов-ти – n).