44. Геометрическое решение биматричных игр 2×2

Пусть имеется игра с матрицей А

	B1	B2
A1	a11	a12
А2	a21	a22

Алгоритм «А»

1.Берем горизонтальный отрезок [0,1].

( )

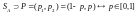2.В концах отрезка [0,1] проводим к нему два перпендикуляра: левый, соответствующий чист. стратегии , и правый- .

3.На левом перпендикуляре от его пересечения с отрезком [0,1] в точке 0 откладываем элементы первой строки матрицы А.

4.На правом перпендикуляре от его пересечения с отрезком [0,1] в точке 1 откладываем элементы 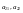второй строки матрицы А.

5.Соединяем точки, изображающие элементы с одинаковыми вторыми индексами (элементы, стоящие в одном и том же столбце матрицы А). В результате получаем отрезки .

Прямые на графике: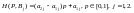

6.Если отрезки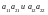 неубывающие: 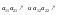, то стратегия доминирует стратегию

Если отрезки возрастающие: , то стратегия строго доминирует стратегию

7.Если отрезок лежит не ниже отрезка , то стратегия доминирует стратегию

Если отрезок лежит выше отрезка , не пересекается с ним, то стратегия строго доминирует стратегию

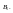
8. Показатель эффективности смешанной стратегии Р=(1-р,p)

- это функция от р, являющаяся нижней огибающей функции Н(Р, В₁) и Н(Р, В₂) (отрезков соответственно).

9.Находим наивысшие точки нижней огибающей.

10.Проектируем их ортогонально на горизонтальный отрезок [0,1].

11.Полученные проекции 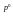определяют оптимальные стратегии игрока А.

12.Ордината наивысшей точки огибающей равна цене игры

= _.

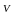13.Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях .

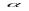14.Нижний из двух верхних концов отрезков есть верхняя цена игры в чистых стратегиях

15.Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка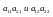 , на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.

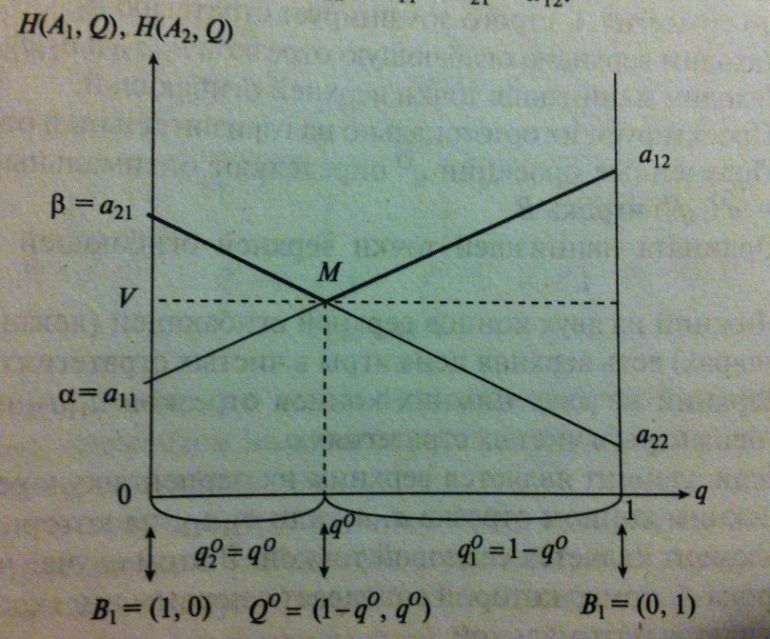
Алгоритм «В»

	B1	B2
A1	a11	a12
А2	a21	a22

1.Берем горизонтальный отрезок [0,1].

2.В концах отр9езка [0,1] проводим к нему два перпендикуляра: левый, соответствующий стратегии B₁ и правый, соответствующий стратегии B₂.

3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем элементы 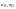первого столбца матрицы А.

4.На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем элементы 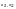второго столбца матрицы А.

5.Соединяем точки, изображающие элементы с одинаковыми первыми индексами (элементы, стоящие в одной и том же строке матрицы А). В результате получаем отрезки .

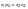6..Находим верхнюю огибающую отрезков .

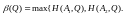
7.Находим наинизшую точку М верхней огибающей.

8.Находим абсциссу наинизшей точки верхней огибающей.

9.Смешанная стратегия является оптимальной стратегией игрока В.

10.Ордината наинизшей точки верхней огибающей и представляет собой цену игры .

11.Нижний из концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях

14.Верхний из двух нижних концов отрезков есть нижняя цена игры в чистых стратегиях

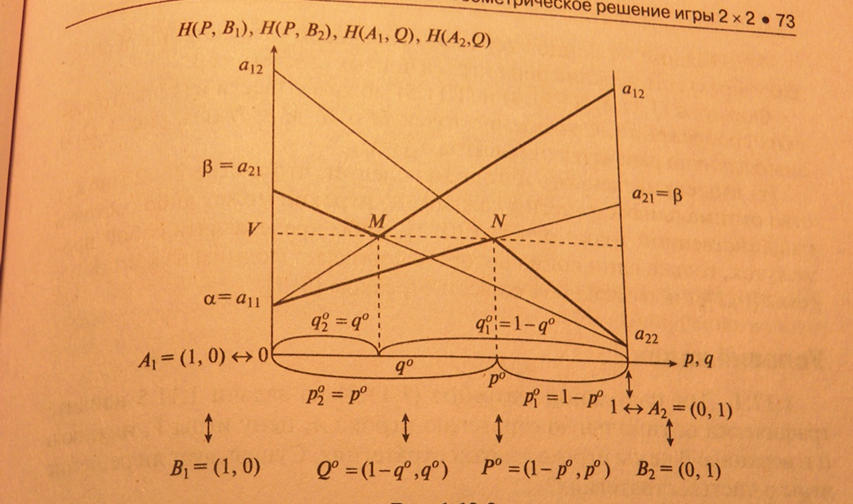
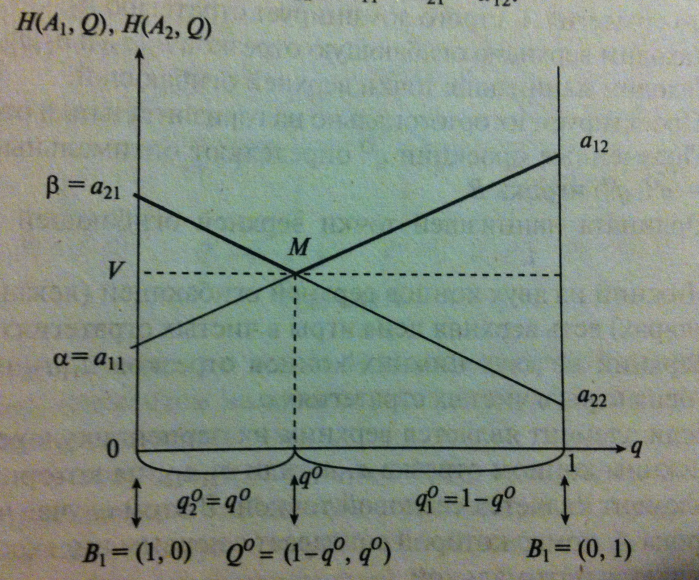
Алгоритм «A,B»

1.Берем горизонтальный отрезок [1,0]

2.В концах отрезка [1,0] проводим к нему два перпендикуляра-левый и правый.

3. На левом перпендикуляре от точки 0 его пересечения с отрезком [1,0] откладываем (как на вертикальной числовой оси)все элементы матрицы А, за исключением элемента а_22.

4.На правом перпендикуляре от точки 1 его пересечения с отрезком [1,0] откладываем все элементы матрица А за исключением а₁₁.

5. Каждый элемент на левом перпендикуляре соединим отрезком каждым элементом на правом перпендикуляре, отлич. от него только одним индексом.

6.Находим нижнюю огибающую.

7.Находим наивысшую точку N нижней огибающей.

8.Находим абсциссу р⁰ наивысшей точки N нижней огибающей.

9. Смешанная стратегия р⁰ = (1-р⁰, р⁰) является оптимальной стратегией игрока А.

10. Находим верхнюю огибающую.

11.Находим наинизшую точку M верхней огибающей.

12. Находим абсциссу q⁰ наинизшей точки М верхней огибающей.

13. Смешанная стратегия Q⁰= (1- q⁰, q⁰) является оптимальной для игрока В.

14.Ордината наивысшей точки N нижней огиб. равна ординате наинизшей точки М верхней огиб. и представляет собой цену игры V.

15.Таким образом, найдено геометрическое решение игры {P⁰,Q⁰,V}

16. Верхний из концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях а.

17.Нижний из концов верхней огиб. (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегия b.