1. Основные понятия и определения теории антагонистических игр.

Игрой называется математическая модель конфликтной ситуации. Раздел теории исследований операций, занимающейся математическими моделями принятия оптимальных решений в условиях конфликта, называется теорией игр.

Заинтересованные стороны в игре называются игроками. Любое возможное в игре действие игрока называется его чистой стратегией.

Игра называется конечной, если множество стратегий каждого игрока конечно.

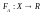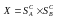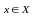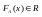Чаще степень удовлетворения интересов игрока А характеризуется его функцией выигрыша , определенной на множестве всех ситуаций и ставящий в соответствие каждой ситуации некоторое число , называемое выигрышем игрока А в ситуации x.

Аналогично, для игрока В функция выигрыша 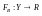определена на множестве 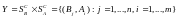ситуаций 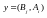и каждый из них ставит в соответствие число 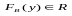, называемое выигрышем игрока В в ситуации y.

Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявления для каждого из них «оптимальных стратегий».

Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимальный возможный средний проигрыш). Выбор оптимальной стратегии базируется на принципе, предполагающем, что оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его цели. Таким образом, теория игр абстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам в реальных случаях.

Если в парной игре игроки преследуют противоположные цели, то игра называется антагонистической. В такой игре один из игроков выигрывает ровно столько, сколько проигрывает другой. Поэтому, функции выигрышей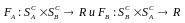 соответственно игроков А и В связаны между собой соотношением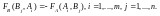 Из этого равенства следует, что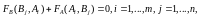 и потому антагонистические игры называют играми двух сторон с нулевой суммой выигрыша.

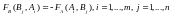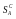В силу равенства функция выигрыша игрока В полностью определяется функцией выигрыша игрока А и, следовательно, антагонистическая игра с игроками А и В определяется совокупностью , состоящей из множества чистых стратегий игрока А, множества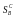 чистых стратегий игрока В и функции выигрыша игрока А.

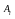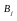В конечной антагонистической игре с игроками А и В можно строки некоторой матрицы поставить в соответствие стратегиям игрока А, а столбцы – в соответствие стратегиям игрока В. Если на пересечениях строк и столбцов расставить значения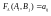 функции выигрыша игрока А, соответствующие ситуации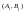 , то получим матрицу А, которая называется матрицей выигрышей игрока А.

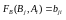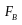Аналогичным образом, из значений функции выигрыша игрока В, можно составить матрицу В выигрышей игрока В. В силу равенства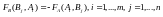 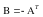. Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.

2. Классификация игр.

Особенностью теории игр как научной дисциплины стала употребляемая в ней специфическая терминология. Термин «игра» применяется для обозначения совокупности правил и соглашений, которыми руководствуются субъекты, поведение которых мы изучаем. Каждый такой субъект k, где k∊l:K, или игрок, характеризуется наличием индивидуальной системы целевых установок и стратегий s₁^k, s₂^k, ...,s_mk^k, т. е. возможных вариантов действий в игре.

Достаточно распространенный способ математического описания игры основан на задании функций f_k (s¹_i1 , s²_i2 , ..., s^k_ik , ..., s^K_ik), каждая из которых определяет результат (платеж, выигрыш), получаемый k-м игроком в зависимости от набора стратегий S = (s¹_i1 , s²_i2 , ..., s^k_ik , ..., s^K_ik), примененного всеми участниками игры. Функции f_k , k∊l:Kтакже называют функциями выигрыша, или платежными функциями.В томслучае, еслидлялюбыхS

игра называется игрой с нулевой суммой. Игры можно классифицировать по числу игроков: парные игры, в которых два игрока, и множественные игры. Если в парной игре игроки преследуют противоположные цели, то игра называется антагонистической.Антагонистические игры, т. е. игры, в которых выигрыш одного участника равен проигрышу другого, в силу относительно простой постановки задачи являются наиболее изученным разделом теории игр. Разделяют и неантагонистические игры. В этих играх выигрыш одного игрока не обязательно означает проигрыш другого. Каждый игрок имеет свою собственную матрицу выигрышей, поэтому часто такие игры называют биматричными (bimatrixgame). Знаменитая теорема Джона Нэша утверждает, что любая игра (антагонистическая или биматричная) с конечным числом чистых стратегий имеет по меньшей мере одну точку равновесия (equilibriumpoint).Однако содержание теории игр, безусловно, не исчерпывается ими. В классификации игровых моделей выделяют игры с конечными и бесконечными наборами стратегий у игроков, выделяют игры по возможным количествам ходов у участников. Также игры делят на некооперативные и кооперативные, т. е. те, в которых функции выигрыша участников зависят от образуемых ими коалиций. Помимо этого игры можно различать по объему информации, имеющейся у игроков относительно прошлых ходов. В этой связи они делятся на игры с полной и неполной информацией. Так же существуют игры с природой. В игре с природой осознанно действует только один игрок, а именно, лицо, принимающее решение; обозначим его через А. Природа, обозначим его через П, является вторым игроком, но не противником игрокаА, а принимает неопределенным образом то или иное свое состояние, не преследуя конкретной цели и безразлично к результату игры. ИгрокаА в игре с природой называют иногда статистиком, а теорию игр с природой – теорией статистических решений.