Модуль №2. Лист контролю.

1. Співвідношення між сторонами і кутами в прямокутному трикутнику.

2. Радіан. Радіанна міра деяких кутів.

3. Означення тригонометричних функцій числового аргументу.

4. Знаки тригонометричних функцій. Значення тригонометричних функцій деяких кутів.

5. Властивості тригонометричних функцій, (парність, періодичність).

6. Формули залежності між тригонометричними функціями одного і того ж аргументу.

7. Формули додавання.

8. Формули зведення.

9. Формули подвійного кута.

10. Формули половинного кута.

11. Формули перетворення добутку тригонометричних функцій в алгебраїчну суму.

12. Формули перетворення алгебраїчної суми тригонометричних функцій в добуток.

13. Властивості та графіки тригонометричних функцій.

14. Обернені тригонометричні функції, їх властивості та графіки.

15. Тригонометричні рівняння.

Література:

1. О.М. Афанасьєва «Математика». 2001р.

2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.

3. М.І. Шкіль «Алгебра і початки аналізу» 10 – 11 кл. 1995р.

4. Н.В. Богомолов «Практические занятия по математике». 1990р.

Тема 3: Степенева, показникові та логарифмічна функції. Їх властивості та графіки.

1. Узагальнення поняття степеня.

2. Властивості степеня.

3. Степенева функція.

4. Показникові функція.

5. Логарифми.

Логарифмічна функція.

1. Узагальнення поняття степеня.

, якщо - натуральне число, .

.

.

,

2. Властивості степеня.

.

.

.

.

.

Властивості коренів.

2. Степенева функція, її властивості та графіки.

Функція виду називається степеневою, де - стале дійсне число.

Властивості:

1. Область визначення;

2. Область значення;

3. Монотонність;

4. Парність;

5. Обереність;

6. Обмеженість;

7. Періодичність;

8. Неперервність.

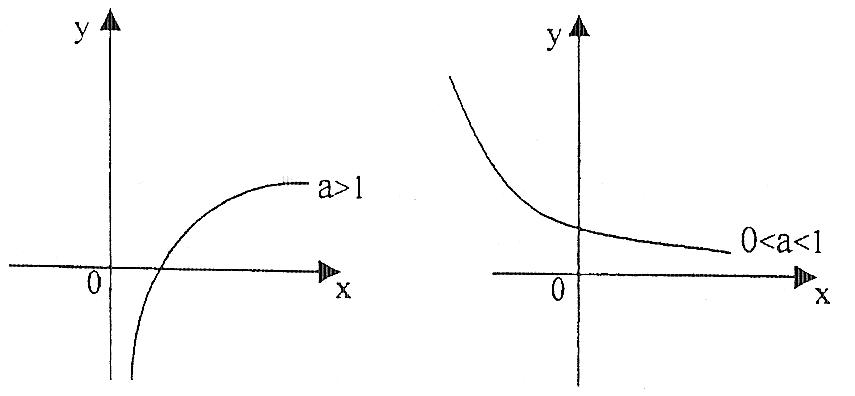
4. Показникові функція, її властивості та графіки.

Функція виду , де , називається показниковою.

Властивості:

1. ;

2. ;

3. При - монотонно зростаюча ; при монотонно спадна ;

4. Обернена;

5. Необмежена;

6. Неперервна;

7. Неперіодична.

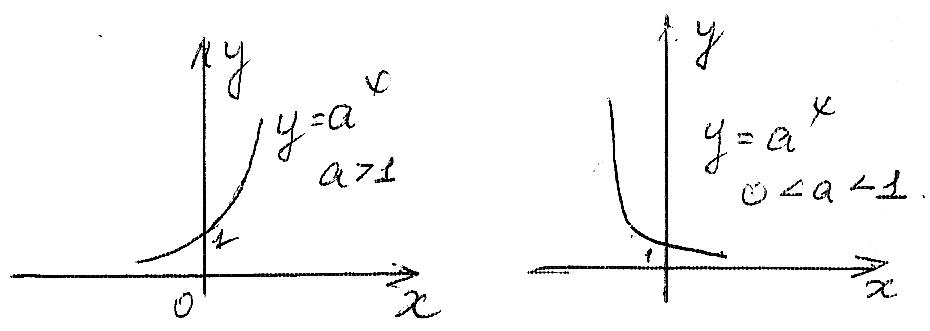
5. Логарифми.

Дія знаходження показника степеня називається дією логарифмування і позначається

Логарифмом числа b за основою а називається показник степеня с, до якого слід піднести основу а, щоб отримати число b. .

основна логарифмічна тотожність.

Основні властивості логарифмів: якщо , то;

Формула переходу від однієї основи логарифма до іншої

;

6. Логарифмічна функція, її властивості та графіки.

Функція, обернена до показникової, називається логарифмічною, , де

Властивості:

1. ;

2. ;

3. Якщо монотонна зростаюча,

якщо монотонна спадна;

4. Функція загального виду;

5. Обернена;

6. Необмежена;

7. Неперервна;

8. Неперіодична.